原标题:Iconfont矢量图标库在网站中的使用方法
大家都知道现在移动端网站设计比较热门,由于移动端的网站页面的收缩性要求很高,必然在网页设计中,一些小点的图标,使用图片收缩性,以及美观上并不是很理想;下面给大家分享一下iconfont矢量图标(字体图标)如何在网页中使用
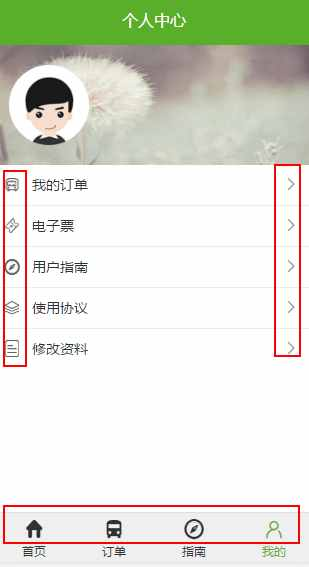
如上图中使用到的都是iconfont图标,使用起来非常方便,随时可以自由的修改你想要的大小和颜色等等!
Iconfont是阿里巴巴推出的矢量图标库,其中涵盖了1000多个常用图标,并在持续更新中。
iconfont图标的优势:
自由变化大小(高清屏无压力)
自由修改颜色(纯色)
可以添加一些视觉效果,如:阴影、旋转、透明度等
iconfont图标在网站中的使用方法:
在iconfont的官网中调用iconfont图标的方法很多,在项目中我就常用unicode引用方法,
第一步:拷贝项目下面生成的font-face

第二步:定义使用iconfont的样式

第三步:挑选相应图标并获取字体编码,应用于页面
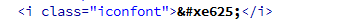
就这简单的三步就能做出你想要的字体图标了,但是有很多小伙伴肯定会有疑问还不知如何使用(特别是刚接触字体图标的小伙伴)所以今天我还得用一个实例来教大家如何在网页中显示字体图标,官网的知识只能教你如何加载文件而实操的话就得靠自己摸索了!
首先我想做一个底部导航栏,如下(有4个小图标)

要想展示这些图标,首先想到的是要去iconfont官网搜索好图标然后下载到本地文件夹中!

输入你想要搜索的图标
比如说搜索“首页”然后就有很多图标展示出来,选择你想要的,然后点击购物车的图标添加入库

选好后到自己的购物车里可以看到如下图所示,自己就新建一个项目文件用来管理好在哪个项目下的字体图标

在自己的项目里可以看到添加好的图标,然后点击下载至本地,就完成了图标的下载

在自己的html项目下新建一个font文件夹,用来存放下载下来的字体图标文件:
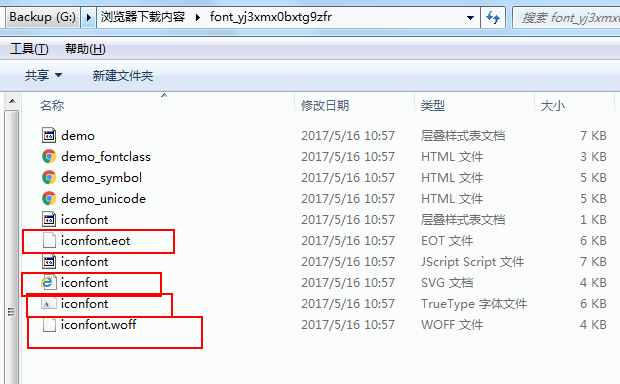
在下载好的字体图标文件中选择以下4个文件拷贝到html下的font目录下即可:
现在就可以来定义自己的字体图标样式和布局了:
html:

用来装字体图标的标签记得加上类 class="iconfont"才能显示字体图标;字体编码可以到iconfont中你自己新建好的项目里查找
css:
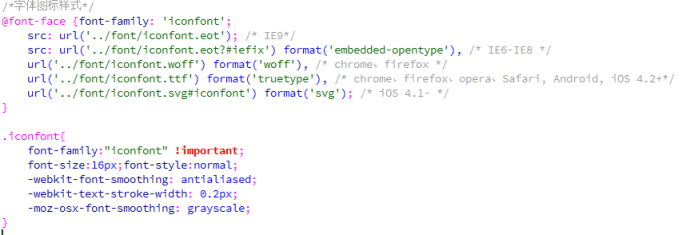
这两部分记得写上,如果怕忘记添加,你们可以放在你的公用css样式里

这样就可以自定义加载的图标的大小和颜色了,因为字体图标就是一个字体,所有可以把它当成是字体那样调整样式即可!返回搜狐,查看更多
责任编辑:
 试题)



)





 试题)
)



)



