
Skip-gram
标签(空格分隔):NLP

一. skip-gram和cbow的对比
skip-gram与cbow相比,好处在于对于不常用的词,skip-gram的效果要更好;
举个简单的例子,一个句子'w1w2w3w4',window_size=1;
对于cbow,模型学习的是预测给定上下文后出现word的概率,或者去最大化下面式子的概率值:
但这对不常见的单词来说是个问题,因为不常见的单词在给定的上下文中不经常出现,结果模型会分配给它们很小的概率。
对于skip-gram,模型学习的是给定单词后去预测上下文的概率,或者去最大化下面式子的概率值:
在这个例子中,两个单词(频繁出现的和不频繁出现的) 被相同的对待。均被当作是单词和上下文两个观测。因此,这个模型会把罕见的单词也学到。
二. skip-gram
主要思想
- 目标:skip-gram目标是通过最优化邻域保留的似然目标,来学习单词的连续特征表示;
- 假设:skip-gram的目标是基于分布假说,其中陈述的是近似上下文中的单词有具有近似含义的趋势。那就是说,相似的单词有着出现在相似邻域内的趋势;
- 算法:遍历文档中的每个单词,对于每个单词,其力求去嵌入单词的特征,以能够去预测邻近的单词(单词在上下文单词的窗口里)。通过使用带负采样的SGD梯度下降,来优化似然函数,学习单词的特征表示。
skip-gram公式化的表述
skip-gram通过最优化似然目标函数,来学习预测给定单词后的上下文。假设现在我们有一个句子:
'I am writing a summary for NLP.'
这个模型目的是,根据给定目标word ‘summary’,来预测window_size=2窗口中的上下文单词;
'I am [] [] summary [] [].'
接着模型试着去最优化似然函数:
事实上,给出一个句子,skip-gram可以做到。相反的,把每个单词都当作一个目标word,并且预测上下文word。所以这个目标函数可以表示为:
给它一个更正式的表述:给出一组单词w和它们的上下文c. 我们考虑条件概率是P(c|w), 并且给出预料,目标是找出条件概率
或者,我们也可以将其写为:
其中D是我们提取的所有单词和上下文的集合,接下来通过log函数来进行简化:
那么接下来的问题就是如何来定义
一是
二是
一个自然的方法是使用softmax函数,所以可以这样来定义:
在这篇文章中,我们假设目标单词w和上下文c来自不同的词汇表矩阵V和U,因此,来自单词word的'lunch'和来自单词上下文的'lunch'是不同的。其中一个动机是每个单词在模型中充当了两种角色,其中一个作为目标单词,而另一个作为上下文单词。这就是为什么我们需要两个单独矩阵的原因,注意到它们必须是相同的维度:V * k,其中k是一个超参数,表示的是每一个词向量的维数。我们想要设置参数
这里我们用内积(inner product)来衡量
(note:将余弦相似度和内积来作为距离度量的对比,cos距离只关心角度的区别,而内积关心的是角度和大小。如果你归一化了你的数据使得它们有相同的大小,那么这两种方法就没有区别了)
代入我们的定义
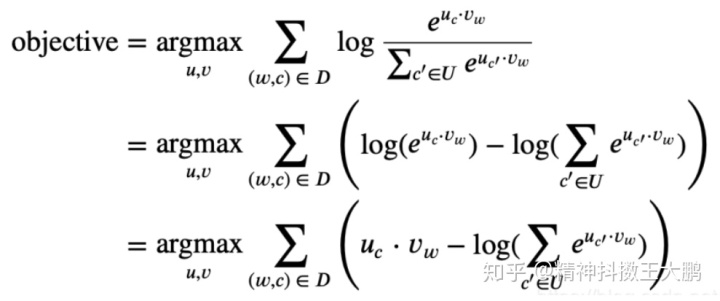
然而这个目标函数计算起来太过于复杂,因为其表示为log(sum),故计算目标函数的代价会比较大。
在考虑所有word的上下文的情况下,其时间复杂度为O(|Vocab|)
为什么更prefer选择在求和里面取log,而不是在求和外面取log
经常我们选择在求和里面取log而不在外面。当你想做优化时,log和sum函数是一部分功能。
这就表示在某个点处,你需要把函数的梯度设为0,导数是线性的计算,所以当你需要求log(sum)时,和的导数就是导数的和。对比之下,根据链式法则,和的log的导数,求得为如下形式:
1/(your sum)⋅(derivative of the sum)
特别是当分析的时候, 找到该函数的0可能是一个具有挑战性的任务。另一方面,因为这个过程的计算代价很大,在求和外的log常常需要近似的来进行计算,例如使用Jensen不等式来进行近似。
现在,开始重新构造目标函数并且对其近似:
负采样--skipgram model
在进行skip-gram模型的推导之前,我们假定(w,c)在训练数据集中是一个词与其上下文词的对,那么
和以前一样,假设有参数
现在的目标变成了寻找参数
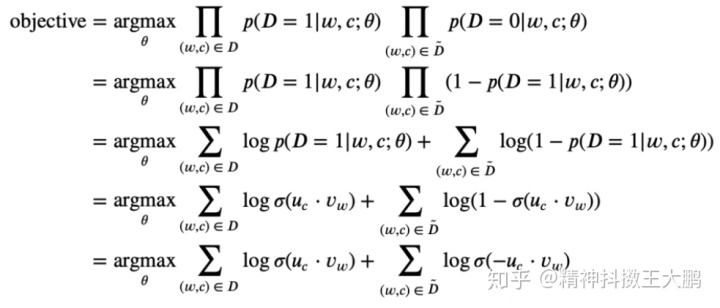
其中
- 1-
=
;
- 该目标函数看起来和逻辑回归的目标函数非常相似;
- 避免了log(sum)的计算;
通常情况下:
因此如果我们对每个数据样本取k个负样本,并且通过N(w)来表示这些负样本。那么目标函数可以表示为:
SGD for skip-gram objective function

代码实现细节
- 动态窗口大小:使用的窗口大小是动态的,参数k表示最大窗口大小。对于语料库中的单词,窗口大小从[1,k]均匀采样;
- 二次采样和稀有词修剪:关于二次采样和下采样
References
https://blog.csdn.net/Jay_Tang/article/details/105577295 唐兄的blog
http://www.davidsbatista.net/blog/2018/12/06/Word_Embeddings/
https://www.quora.com/Why-is-it-preferential-to-have-the-log-inside-the-sum-rather-than-outside
- END -


多线程)



服务器基础编程)


libevent实现高性能网络服务器)


各流媒体服务器的比较)


mediasoup服务器的布署与使用)



mediasoup的信令系统)