理论基础
之前我们介绍了强化学习
Leo:和Leo一起学量子计算:三点一. 微分线路和强化学习zhuanlan.zhihu.com
上面这篇博文告诉我们如何把量子线路类比为神经网络,并获取它的导数。在可微分线路的基础上,我们可以做一些更加酷的事情,比如量子对抗学习。
2018年,量子机器学习领域出现了几篇夺人眼球的关于量子对抗生成学习的文章,它们分别是
- Seth Lloyd, Christian Weedbrook
- [1804.09139] Quantum generative adversarial learning
- Quantum generative adversarial networks
- [1804.08641] Quantum generative adversarial networks
- Benedetti, M., Grant, E., Wossnig, L., & Severini, S.
- [1806.00463] Adversarial quantum circuit learning for pure state approximation
- Haozhen Situ, Zhimin He, Lvzhou Li, Shenggen Zheng
- [1807.01235] Quantum generative adversarial network for generating discrete data
- Jinfeng Zeng,Yufeng Wu,Jin-Guo Liu,Lei Wang,Jiangping Hu
- [1808.03425] Learning and Inference on Generative Adversarial Quantum Circuits
理论基础
下面简单介绍下第三篇工作的基本思想,也就是今年 6 月份的这篇学习纯态波函数的文章, 他是对第一篇和第二篇文章思想的传承和简化版本。这篇文章要解决的问题是,给定一个未知量子线路T,它可以让波函数从
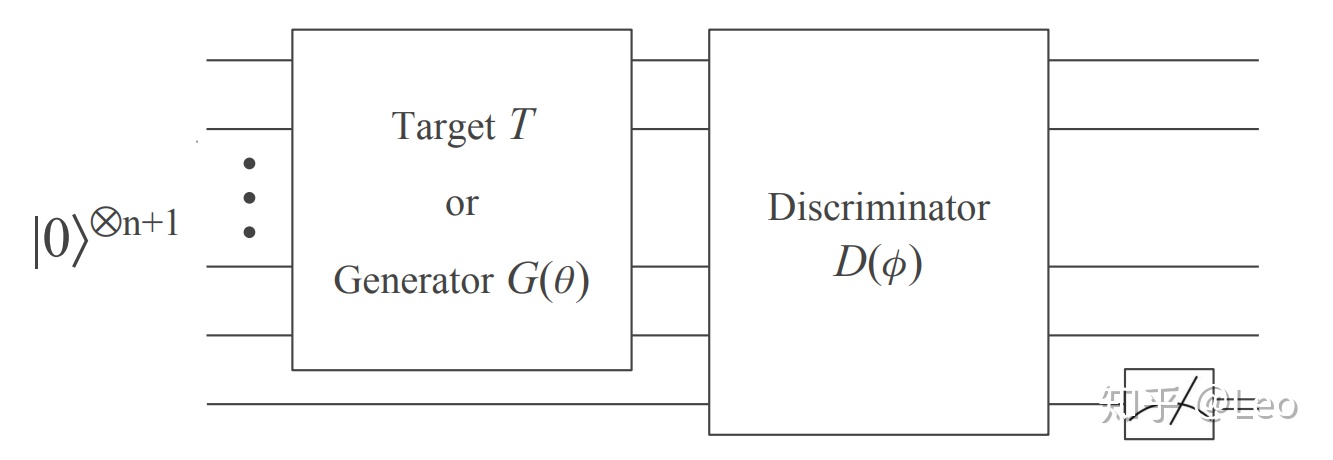
如图1所示,QuGAN 的量子线路主体包括两个部分,生成线路和判别线路,生成线路尽量去仿制T线路的波函数以达到以假乱真的效果,而判别器则通过一个量子线路尽可能的仅通过辅助比特的测量知道输入的波函数是真还是假。Loss函数可以写作
其中,
具体的线路细节以及Loss函数的描述请见arXiv: 1806.00463。
代码实现
首先申明下,Yao最近将会发布0.3更新,会有更加丰富的API和GPU的支持。但是也面临着API不稳定的问题,建议安装master分支 ]add Yao#master 以及`]add QuAlgorithmZoo#master`。如果在尝试实现Tutorial代码的过程中遇到了问题,请以知乎评论或者issue的形式反馈。我会在发布0.3版本后系统的更新这个系列的代码。
using LinearAlgebrausing Yao
using QuAlgorithmZoo: random_diff_circuit, pair_ring"""
Quantum GAN.Reference:Benedetti, M., Grant, E., Wossnig, L., & Severini, S. (2018). Adversarial quantum circuit learning for pure state approximation, 1–14.
"""
struct QuGAN{N}target::ArrayReggenerator::AbstractBlock{N}discriminator::AbstractBlockreg0::ArrayRegwitness_op::AbstractBlockcircuit::AbstractBlockgdiffsddiffsfunction QuGAN(target::DefaultRegister, gen::MatrixBlock, dis::MatrixBlock)N = nqubits(target)c = Sequence([gen, addbits!(1), dis])witness_op = put(N+1, (N+1)=>ConstGate.P0)gdiffs = chain(collect_blocks(AbstractDiff, gen))ddiffs = chain(collect_blocks(AbstractDiff, dis))new{N}(target, gen, dis, zero_state(N), witness_op, c, gdiffs, ddiffs)end
end首先,申明QuGAN结构体,其中witness_op是loss中的
gdiffs和ddiffs分别记录了生成器和判别器的微分模块,这些微分模块可以用collect函数来自动获取,该函数做的事情是对Block Tree做深度有限的搜索,把特定类型的gate放入sequence里面并返回。 整个线路(变量circuit)包含生成器,增加一个qubit,判别器三部分。"""loss function"""
loss(qcg::QuGAN) = p0t(qcg) - p0g(qcg)
"""probability to get evidense qubit 0 on generation set."""
p0g(qg::QuGAN) = expect(qg.witness_op, psi_discgen(qg)) |> real
"""probability to get evidense qubit 0 on target set."""
p0t(qg::QuGAN) = expect(qg.witness_op, psi_disctarget(qg)) |> real
"""generated wave function"""
psi(qg::QuGAN) = copy(qg.reg0) |> qg.generator
"""input |> generator |> discriminator"""
psi_discgen(qg::QuGAN) = copy(qg.reg0) |> qg.circuit
"""target |> discriminator"""
psi_disctarget(qg::QuGAN) = copy(qg.target) |> qg.circuit[2:end]
"""tracedistance between target and generated wave function"""
distance(qg::QuGAN) = tracedist(qg.target, psi(qg))[]p0g函数计算Loss中的第二项
p0t则计算Loss中第一项
我们用trace distance作为衡量训练结果的好坏的最终标准。但trace distance实验的操作性不强,这时候可以用swap test来计算两个态的overlap,也是不错的选择。
"""obtain the gradient"""
function grad(qcg::QuGAN)ggrad_g = opdiff.(()->psi_discgen(qcg), qcg.gdiffs, Ref(qcg.witness_op))dgrad_g = opdiff.(()->psi_discgen(qcg), qcg.ddiffs, Ref(qcg.witness_op))dgrad_t = opdiff.(()->psi_disctarget(qcg), qcg.ddiffs, Ref(qcg.witness_op))[-ggrad_g; dgrad_t - dgrad_g]
end"""the training process"""
function train(qcg::QuGAN{N}, g_learning_rate::Real, d_learning_rate::Real, niter::Int) where Nng = length(qcg.gdiffs)for i in 1:niterg = grad(qcg)dispatch!(+, qcg.generator, -g[1:ng]*g_learning_rate)dispatch!(-, qcg.discriminator, -g[ng+1:end]*d_learning_rate)(i*20)%niter==0 && println("Step = $i, Trance Distance = $(distance(qcg))")end
end量子线路对于可观测量的微分可以见三点一章节的讨论。
在训练中,这里简单的给generator和discriminator定了两个不同的learning rate,但是梯度方向是相反的。生成器会往下降 loss 的方向训练, 而判别器则往提升 loss 的方向训练, 判别器的 learning rate 一般要高一点才有助于收敛. 其实更加妥当的做法是, 内部加一个对discriminator的训练的loop,保证discriminator总是收敛。
nbit = 3
target = rand_state(nbit)
gen = dispatch!(random_diff_circuit(nbit, 2, pair_ring(nbit)), :random) |> autodiff(:QC)
discriminator = dispatch!(random_diff_circuit(nbit+1, 5, pair_ring(nbit+1)), :random) |> autodiff(:QC)
qcg = QuGAN(target, gen, discriminator)
train(qcg, 0.1, 0.2, 1000)这里尝试学习一个3 qubit的量子随机态, 生成和判别用的线路深度分别为 2 和 5, 学习速率分别是 0.1 和 0.2. 如果运行顺利,将会看到如下结果
Step = 50, Trance Distance = 0.6342280675404924
Step = 100, Trance Distance = 0.2556083335074918
Step = 150, Trance Distance = 0.20588883282356
Step = 200, Trance Distance = 0.18588876599788512
Step = 250, Trance Distance = 0.14383386098057532
Step = 300, Trance Distance = 0.11122073204131669
Step = 350, Trance Distance = 0.12055174236882853
Step = 400, Trance Distance = 0.08476938309711918
Step = 450, Trance Distance = 0.055730139169513575
Step = 500, Trance Distance = 0.0658058630141474
Step = 550, Trance Distance = 0.030654404721949198
Step = 600, Trance Distance = 0.05670115284050363
Step = 650, Trance Distance = 0.026043726656018153
Step = 700, Trance Distance = 0.03717624105785262
Step = 750, Trance Distance = 0.018583002816583323
Step = 800, Trance Distance = 0.038243650242252694
Step = 850, Trance Distance = 0.02220738846752642
Step = 900, Trance Distance = 0.016162779109655048
Step = 950, Trance Distance = 0.0070184081980637705
Step = 1000, Trance Distance = 0.016831931463320904我们发现trace distance的确可以下降,可以学到目标状态,但是收敛的并不快。也是所有基于GAN的方法的通病吧~
这里谈一下 QuGAN 的优点和缺点, 优点是结构简单, 形式也很酷, 有很多可以继续玩的东西. 缺点也很明显.
首先文章里面用到的 loss 和经典 GAN 的 loss 其实不一样, 这种不一样是由于求导方案必须要求最终的输出为可观测量这个约束导致的. 这也是为什么 arXiv: 1807.01235 和 arXiv: 1808.03425 会采用量子经典的对抗学习的方案.
其次, 这里的生成型模型生成的是量子力学波函数, 一般生成型包括很多量子生成型模型的目标都是得到经典数据, 比如 arXiv: 1804.04168中提到的 Born Machine. 但是这里连同波函数相位一起学习了, 学习难度也高了很多, 作为经典数据的生成器是做了无用功的. 但也要考虑到它的应用场景不一样.
最后, 所有 GAN 的通病, Modal Collapse, 收敛慢, 它都有, 所有量子变分线路的通病, 比如求导复杂度高 (比如经典深度学习 BP 方案的O(N), 它是O(N^2), 其中 N 为参数个数), 它也有.
虽然有这么多缺点, 但是毫无疑问, 它为理论学家们提供了很不错的新玩具!

)

















