👨‍🎓作者简介：一位即将上大四，正专攻机器学习的保研er
🌌上期文章：机器学习&&深度学习——常见循环神经网络结构（RNN、LSTM、GRU）
📚订阅专栏：机器学习&&深度学习
希望文章对你们有所帮助

注意力提示

引入

之前讲过的CNN和RNN模型，容易发现的一个点是，他们并没有刻意的、主观的针对某个点去做训练和预测，这是因为他们并没有注意力。讲到注意力我们就要知道心理学中的非自主性提示和自主性提示。
什么叫非自主性提示呢？举个例子，一群杀马特中间的老大是个光头，根本不需要别人告知你，你就会觉得这人很突兀，很不一般，也就是说人的注意力没有受到认知和意识的控制。
而自主性提示就是人的注意力受到认知和意识的控制，因此注意力在基于自主性提示去辅助选择时将更为谨慎。受试者的主观意愿推动，选择的力量也就更强大。

查询、键和值

自主性的与非自主性的注意力提示解释了人类的注意力的方式，下面来看看如何通过这两种注意力提示，用神经网络来设计注意力机制的框架：
首先，考虑简单的非自主性提示。要想将选择偏向于感官输入，可以简单使用参数化的全连接层，甚至是非参数化的最大池化层或平均池化层。
所以，“是否包含自主性提示”将注意力机制与全连接层或池化层区别开来。
在注意力机制下，自主性提示被称为查询（给定任何查询，注意力机制通过注意力池化将选择引导至感官输入）。在注意力机制中，这些感官输入被称为值，每个值都有一个键配对，可以想象成感官输入的非自主性提示。如下所示：

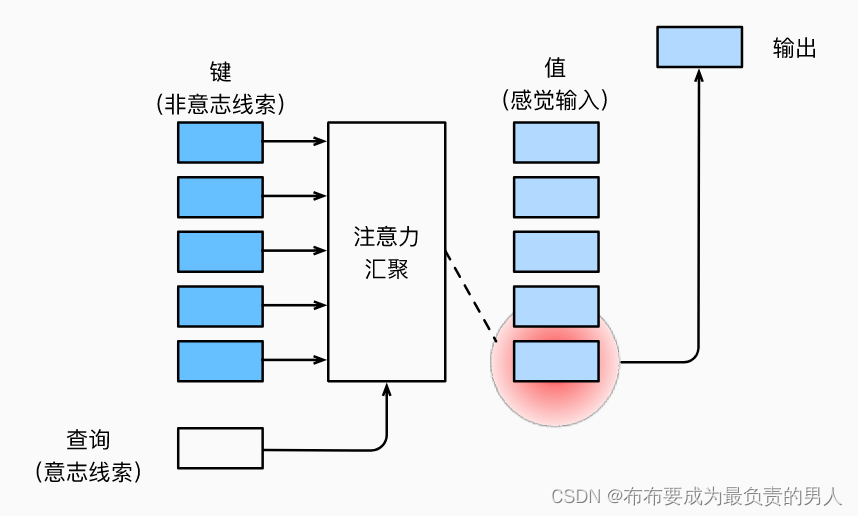
注意：汇聚就是池化。

注意力的可视化

平均池化层可以被视为输入的加权平均值，其中各输入的权重是一样的。实际上，注意力池化得到的是加权平均的总和值，其中权重是在给定的查询和不同的键之间计算得出的。
下面来进行注意力可视化，我们通过热力图的方式来展示，定义一个show_heatmaps，其输入matrices的形状是（要显示的行数，要显示的列数，查询的数目，键的数目）。

import torch
from d2l import torch as d2l#@save
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),cmap='Reds'):"""显示矩阵热图"""d2l.use_svg_display()num_rows, num_cols = matrices.shape[0], matrices.shape[1]fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,sharex=True, sharey=True, squeeze=False)for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):pcm = ax.imshow(matrix.detach().numpy(), cmap=cmap)if i == num_rows - 1:ax.set_xlabel(xlabel)if j == 0:ax.set_ylabel(ylabel)if titles:ax.set_title(titles[j])fig.colorbar(pcm, ax=axes, shrink=0.6)

用简单例子来演示一下：仅当查询和键相同时，注意力权重为1，否则为0

attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
d2l.plt.show()

输出结果：

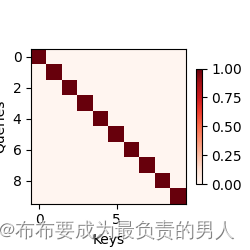
小结

1、人类的注意力是有限的、有价值和稀缺的资源。
2、使用非自主性和自主性提示有选择性地引导注意力，前者基于突出性，后者则依赖于意识。
3、注意力机制与全连接层或者池化层的区别源于增加的自主提示。
4、由于包含了自主性提示，注意力机制与全连接的层或池化层不同。
5、注意力机制通过注意力池化使选择偏向于值（感官输入），其中包含查询（自主性提示）和键（非自主性提示）。键和值是成对的。
6、可视化查询和键之间的注意力权重是可行的。

注意力池化：Nadaraya-Watson核回归

上面已经介绍了注意力机制的主要成分：查询（自主提示）和键（非自主提示）之间的交互形成了注意力池化。注意力池化有选择地聚合了值（感官输入）以生成最终的输出。后面将会以简单例子来进行讲解。

import torch
from torch import nn
from d2l import torch as d2l

生成数据集

简单起见，考虑下面这个回归问题：给定的成对的“输入－输出”数据集，如何学习f来预测任意新输入的x，其输出y_hat=f(x)。
生成一个人工数据集，加入噪声项σ：
$$y_i=2sin(x_i)+x_i^{0.8}+\sigma$$
其中σ服从均值为0，标准差0.5的正态分布。在这里生成了50个训练样本和50个测试样本。为了更好地可视化之后的注意力模式，需要将训练样本进行排序。

import torch
from torch import nn
from d2l import torch as d2ln_train = 50  # 训练样本数
x_train = torch.sort(torch.rand(n_train) * 5)[0]   # 排序后的训练样本def f(x):return 2 * torch.sin(x) + x**0.8y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,))  # 训练样本的输出
x_test = torch.arange(0, 5, 0.1)  # 测试样本
y_truth = f(x_test)  # 测试样本的真实输出
n_test = len(x_test)  # 测试样本数

下面函数将绘制所有的训练样本（圆圈表示），不带噪声项的真实数据生成函数f（标记为Truth），以及学习得到的预测函数（标记为Pred）：

def plot_kernel_reg(y_hat):d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])d2l.plt.plot(x_train, y_train, 'o', alpha=0.5)

平均池化

其表达式为：
$$f(x)=\frac{1}{n}\sum _{i=1}^n{y}_i$$
在绘制预测结果之前，先介绍一下repeat_interleave函数，可以看下面的这一篇博客，看懂用法：
【PyTorch】repeat_interleave()方法详解
现在我们可以绘制预测结果：

y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)
d2l.plt.show()

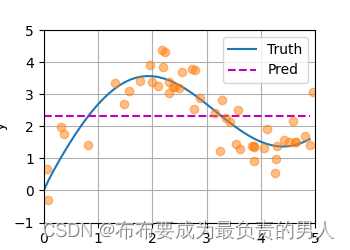
可以发现真实函数和预测函数的差距很大，并不是很好的方式。

非参数注意力池化

很显然，平均池化只注意y而没有注意x，于是提出了更好的想法，根据输入的位置对输出y进行加权：
$$f(x)=\sum _{i=1}^n\frac{K(x-x_i)}{{\sum }_{j=1}^{n}K(x-x_j)}{y}_i$$
其中K是核，上面的估计器被称为Nadaraya-Watson核回归。我们可以从注意力机制的框架角度重写上式，成为一个更通用的注意力池化公式：
$$\begin{gathered} f(x)=\sum _{i=1}^n\alpha (x,x_i)y_i \\ 其中，x是查询，(x_i,y_i)是键值对 \end{gathered}$$
显然，注意力池化就是yi的加权平均，将查询x和键xi之间的关系建模为注意力权重α。容易知道，对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布：它们是非负的，并且总和为1。
比如，我们可以考虑一个高斯核，定义为：
$$K(u)=\frac{1}{\sqrt{2\pi }}exp(-\frac{u^2}{2})$$
将高斯核带入上式，得：
$$\begin{gathered} f(x)=\sum _{i=1}^n\alpha (x,x_i)y_i \\ =\sum _{i=1}^n\frac{exp(-\frac{1}{2}(x-x_i{)}^2)}{{\sum }_{j=1}^{n}exp(-\frac{1}{2}(x-x_j{)}^2)}{y}_i \\ =\sum _{i=1}^{n}softmax(-\frac{1}{2}(x-x_i{)}^2)y_i \end{gathered}$$
可以看出，如果一个键xi越是接近给定的查询x，那么分配给这个键对应值的yi的注意力权重就会越大，也就“获得了更多的注意力”。
需要注意，Nadaraya-Watson核回归是一个非参数模型，也因此，上式是非参数的注意力池化模型。基于该模型绘制预测结果，可以发现预测线是平滑的，且比平均池化的预测更接近真实：

# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入（例如：同样的查询）
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
# x_train包含着键。attention_weights的形状：(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值（y_train）之间分配的注意力权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值，其中的权重是注意力权重
y_hat = torch.matmul(attention_weights, y_train)
plot_kernel_reg(y_hat)
d2l.plt.show()

运行结果：

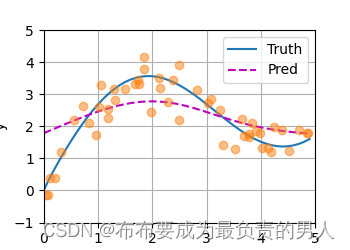
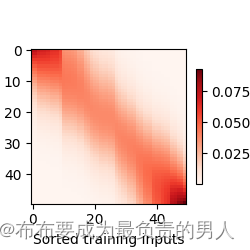
现在我们来观察注意力的权重。这里测试数据的输入相当于查询，而训练数据的输入相当于键。因为两个输入都是经过排序的，因此由观察可知“查询-键”对越接近，注意力汇聚的注意力权重就越高：

# unsqueeze(0)表示增加第一维度，增加两次维度
d2l.show_heatmaps(attention_weights.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')
d2l.plt.show()

运行结果：

带参数注意力池化

非参数的Nadaraya-Watson核回归具有一致性的优点：若有足够数据，该模型会收敛到最优结果。尽管如此，我们还是可以轻松地将可学习的参数集成到注意力池化中。
与之前不同，在下面的查询x和键xi之前的距离乘以可学习的参数w：
$$\begin{gathered} f(x)=\sum _{i=1}^n\alpha (x,x_i)y_i \\ =\sum _{i=1}^n\frac{exp(-\frac{1}{2}((x-x_i)w{)}^2)}{{\sum }_{j=1}^{n}exp(-\frac{1}{2}((x-x_j)w{)}^2)}{y}_i \\ =\sum _{i=1}^{n}softmax(-\frac{1}{2}((x-x_i)w{)}^2))y_i \end{gathered}$$
下面将通过训练这个模型来学习注意力汇聚的参数。

批量矩阵乘法

对于矩阵乘法，我们之前已经知道对于两个形状分别为a×b和b×c的矩阵，进行矩阵乘法以后矩阵的形状就变成a×c的，现在做个推广，假设两个张量的形状分别为n×a×b和n×b×c，则进行批量矩阵乘法后，输出n×a×c。
在注意力机制的背景中，我们可以使用小批量矩阵乘法来计算小批量数据中的加权平均值。

weights = torch.ones((2, 10)) * 0.1
values = torch.arange(20.0).reshape((2, 10))
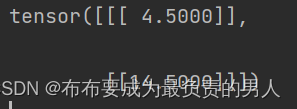
print(torch.bmm(weights.unsqueeze(1), values.unsqueeze(-1)))

输出结果：

定义模型

使用小批量矩阵乘法，定义Nadaraya-Watson核回归的带参数版本为：

class NWKernelRegression(nn.Module):def __init__(self, **kwargs):super().__init__(**kwargs)self.w = nn.Parameter(torch.rand((1,), requires_grad=True))def forward(self, queries, keys, values):# queries和attention_weights的形状为(查询个数，“键－值”对个数)queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))self.attention_weights = nn.functional.softmax(-((queries - keys) * self.w)**2 / 2, dim=1)# values的形状为(查询个数，“键－值”对个数)return torch.bmm(self.attention_weights.unsqueeze(1),values.unsqueeze(-1)).reshape(-1)

训练

将训练数据集变换为键和值用于训练注意力模型，在带参数的注意力汇聚模型中，任何一个训练样本的输入都会和除自己以外的所有训练样本的“键－值”对进行计算，从而得到其对应的预测输出。

训练带参数的注意力汇聚模型时，使用平方损失函数和随机梯度下降。

# X_tile的形状:(n_train，n_train)，每一行都包含着相同的训练输入
X_tile = x_train.repeat((n_train, 1))
# Y_tile的形状:(n_train，n_train)，每一行都包含着相同的训练输出
Y_tile = y_train.repeat((n_train, 1))
# keys的形状:('n_train'，'n_train'-1)
keys = X_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
# values的形状:('n_train'，'n_train'-1)
values = Y_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))net = NWKernelRegression()
loss = nn.MSELoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
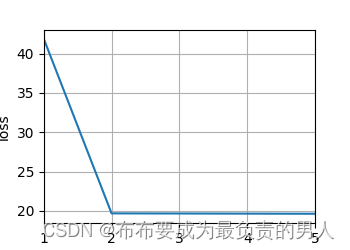
animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])for epoch in range(5):trainer.zero_grad()l = loss(net(x_train, keys, values), y_train)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')animator.add(epoch + 1, float(l.sum()))
d2l.plt.show()

运行结果：

接着绘制预测结果：

# keys的形状:(n_test，n_train)，每一行包含着相同的训练输入（例如，相同的键）
keys = x_train.repeat((n_test, 1))
# value的形状:(n_test，n_train)
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
plot_kernel_reg(y_hat)
d2l.plt.show()

运行结果：

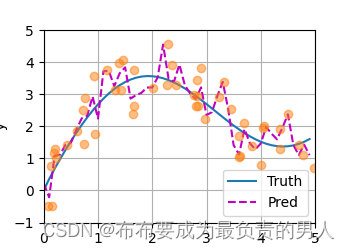
容易发现，在尝试拟合带噪声的训练数据时，预测结果绘制的线不如之前非参数模型的平滑。
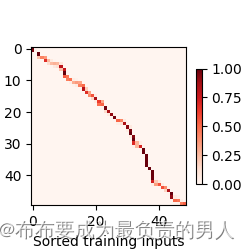
可以尝试查看热力图，带参数的模型加入可学习的参数后，曲线在注意力权重较大的区域变得更不平滑：

d2l.show_heatmaps(net.attention_weights.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')
d2l.plt.show()

运行结果：

小结

1、Nadaraya-Watson核回归是具有注意力机制的机器学习范例。
2、Nadaraya-Watson核回归的注意力池化是对训练数据中输出的加权平均。从注意力的角度来看，分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。
3、注意力池化可以分为非参数型和带参数型。