分布式一致性协议

一、引言

　　在分布式系统中，为了保证数据的高可用，通常会将数据保留多个副本(replica)，这些个副本会放在不同的物理机上，为了对用户提供正确的数据，我们需要保证这些放在不同物理机上的副本是一致的。为了解决这种分布式一致性问题，提出了很多经典的协议和算法，比较著名的是 两阶段提交协议和三阶段提交协议。

二、两阶段提交协议

　　两阶段提交协议把分布式事务分为两个阶段，一个是准备阶段，一个是提交阶段。准备阶段和提交阶段都是由事务管理器发起的，两阶段提交协议的流程如下：

　　1、准备阶段：事务管理器向资源管理器发起指令，资源管理器评估自己的状态，如果资源管理器评估指令可以完成。则会写redo或者undo日志，然后锁定资源，执行操作，但是并不会提交

　　2、提交阶段：如果每个资源管理器明确返回准备成功，事务管理器向资源管理器发起提交指令，资源管理器提交资源变更的事务，释放锁定的资源；如果任何一个资源管理明确返回准备失败，则事务管理器向资源管理器发起中止指令，资源管理器取消已经变更的事务，执行undo日志。释放锁定的资源。

　　

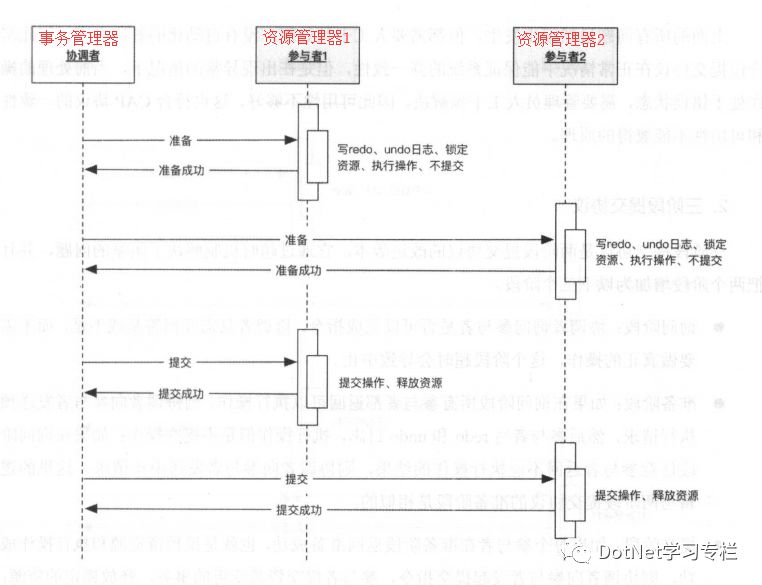
（两阶段提交协议的成功场景图）

　　我们从上图中可以看到，两阶段提交协议在准备阶段锁定资源，这是一个重量级的操作，能保证强一致性，但是实现起来复杂、成本大、不够灵活。还有以下缺点：

　　　  （1）、阻塞：对于任何一次指令都必须收到明确的响应，才会继续进行下一步，否则处于阻塞状态，占用的资源一直被锁定，不会释放

　　　  （2）、单点故障：如果事务管理器（协调者）挂了（宕机），资源管理器（参与者）没有事务管理器（协调者）指挥，则会一直阻塞，尽管可以通过选举新的协调者替代原有的协调者，但是参与者接收后也宕机，则新上任的协调者无法处理这种情况

　　　  （3）、脑裂：协调者发送提交指令，有的参与者接收到并执行了事务，有的参与者没有接收到事务就没有执行事务，多个参与者之间是不一致的。

　　上面的问题虽然很少发生，但每次发生都需要人工参与，没有自动化解决方案，因此两阶段提交协议在正常情况下能保证系统的强一致性，但在出现异常的情况下，需要人工干预解决，因此可用性不够好，其实这也符合CAP协议的一致性和可用性不能兼得的原理。

三、三阶段提交协议

　　三阶段提交协议是两阶段提交协议的改进版本，它通过超时机制解决了阻塞的问题，并且把两个阶段增加为三个阶段。

　　1、询问阶段：事务管理器（协调者）询问参与者（资源管理器）是否可以完成指令，参与者只需要回答是或者否，而不需要做真正的操作，这个阶段超时会导致中止。

　　2、准备阶段：如果在询问阶段所有参与者都返回可以执行操作，则协调者向参与者发送预执行请求，然后参与者写 redo 和 undo 日志，执行操作但不提交操作；如果在询问阶段任何一个参与者返回不能执行操作的结果，则协调者向参与者发送中止请求，这里的逻辑和两阶段提交协议的准备阶段是相似的。

　　3、提交阶段：如果每个参与者在准备阶段返回准备成功，则协调者向参与者发送提交指令，参与者提交资源变更的事务，释放锁定的资源；如果任何一个参与者返回准备失败，则协调者向参与者发送中止指令，参与者自己取消已经变更的事务，执行 undo 日志，释放锁定的资源。这里的逻辑和两阶段提交协议的提交阶段一致。

　　　　

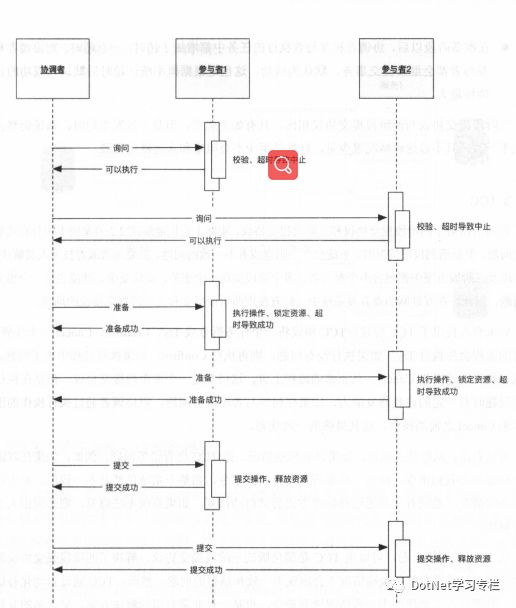
　（三阶段提交协议的成功场景图）

　　三阶段提交协议与两阶段提交协议主要有以下不同点：

　　　　（1）、增加了一个询问阶段，询问阶段可以确保尽可能早地发现无法执行操作而需要中止的行为，但是它并不能发现所有的这种行为，只会减少这种情况的发生。

　　　　（2）、在准备阶段以后，协调者和参与者执行的任务中都增加了超时，一旦超时，则协调者和参与者都会继续提交事务，默认为成功。

　　三阶段提交协议与两阶段提交协议相比，具有以上的优点，但是一旦发生超时，系统仍然会发生不一致，只不过这种情况很少见。好处是不会阻塞和永远锁定资源。　　

四、TCC

　　两阶段和三阶段提交协议，在遇到极端情况时，系统会产生阻塞或者不一致的问题，需要人干预解决。两阶段及三阶段方案中都包含多个参与者、多个阶段实现一个事务。实现事务，性能也是一个很大的问题。因此在互联网的高并发系统中，很少有使用两阶段提交和三阶段提交协议的场景。

　　后来有人提出了TCC协议，TCC协议将一个任务分成 Try、Confirm、Cancel 三个步骤。正常的流程会先执行 Try，如果执行没有问题，则再执行 Confirm，如果执行过程中出现了异常。则执行操作的逆操作 Cancel。从正常的流程上讲。这还是一个两阶段提交协议，但在执行出现异常后有一定的自我修复能力，如果任何参与者出现了问题，则协调者通过执行操作的逆操作来 Cancel 之前的操作。达到最终一致性状态。

　　可以看出，从时序上讲，如果遇到机端情况，则TCC会有很多问题，如：如果在取消时一些参与者收到指令，而另一些参与者没有收到指令，则整个系统任然是不一致的，对于这种复杂的情况，系统首先会通过补偿的方式尝试自我修复，如果系统无法修复。还是需要人工干预解决。

　　从 TCC 的逻辑上来看，它是简化版的三阶段提交协议，解决了两阶段提交协议的阻塞问题，但还是没有解决极端情况下出现的问题（不一致和脑裂问题）。然而，TCC 通过自动化补偿手段，将需要人工处理的不一致问题降到最低，也是一种很有用的解决方案。

                                  

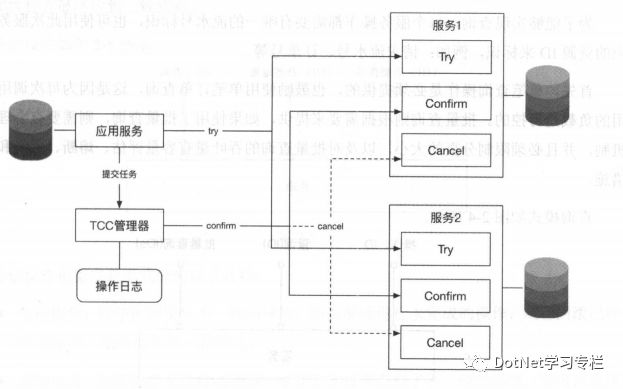
（TCC 协议的使用场景）

说明：

　　1、参考书籍：《分布式服务架构：原理、设计与实战》

　　2、如有不合适的地方请反馈。综合后更改。