在Docker生态系统中除了上一节所讲解的基本概念，还有其他专业术语，本文我们将一笔带过，同时会开始陆续进入到在.NET Core中使用Docker。

专业术语

Docker Engine（Docker引擎）：客户端 - 服务器应用程序。Docker公司将Docker Engine分为两个产品。Docker Community Edition（CE）基于开源工具且免费，我们学习时可以使用这款产品。Docker Enterprise附带了其他功能支持，比如管理和安全等等功能。

Docker Client（Docker客户端）：我们与Docker进行交互的主要方式。使用Docker命令行界面（CLI）时，在终端中键入以docker开头的命令，Docker Client会使用Docker API将命令发送到Docker守护进程中。

Docker Daemon（Docker守护进程）：监听Docker API请求的Docker服务器。Docker守护进程主要管理镜像，容器，网络和卷。

Docker Volumes（Docker卷）：存储创建应用程序和运行应用程序持久化数据的最佳方式。

Docker Registry：存储Docker镜像的远程注册位置。我们将镜像推送到注册表并从注册表中提取图像，我们可以托管自己的注册表或使用供应商商的注册表。

Docker Hub：Docker镜像的最大注册表。它也是Dcoker默认的注册表位置， 我们可以在Docker Hub上找到免费的镜像并存储我们自己的图像。

Docker Networking：允许我们将Docker容器连接在一起。连接的Docker容器可以位于同一主机或多个主机上。

Docker Compose：属于一个工具，我们可以非常轻松地运行需要多个Docker容器的应用程序。Docker Compose允许我们将命令写到docker-compose.yml文件中以供重用。Docker Compose命令行界面（cli）使我们可以更轻松地与多容器应用程序进行交互。Docker Compose免费安装Docker。

Docker Swarm：容器部署编排的产品。Docker官方教程进行容器编排和部署使用的Docker Swarm。建议不要浪费时间在Docker Swarm上，推荐使用Kubernetes(k8s)。

Docker Services：分布式应用程序的不同部分。 服务实际上只是“生产中的容器”。服务只运行一个镜像，但它编码了镜像的运行方式 - 它应该使用哪些端口，容器应该运行多少个副本，以便服务具有所需的容量等等。扩展服务会更改运行该软件的容器实例的数量，从而为流程中的服务分配更多计算资源。Docker服务允许我们跨多个Docker守护进程扩展容器，并使Docker Swarms成为可能。

容器回顾

Docker镜像在构建时被创建，而Dokcer容器在运行时被创建。

Dockerfile是Docker的核心，Dockerfile告诉Docker如何构建镜像从而被用来制作容器，每个Docker镜像都包含一个名为Dockerfile但没有扩展名的文件。

当调用docker build以创建映像时，假定Dockerfile位于当前工作目录中，可以使用文件标志（-f）指定到其他位置，容器是由一系列层所构建，而且每个镜像层只读，除了位于其他镜像层之上的最终容器镜像层。Dockerfile告诉Docker要添加哪些层以及添加它们的顺序，每个镜像层实际上只是一个包含自上一层以来的所更改的文件。

在linux中，几乎所有东西都是文件。基础镜像提供初始层，基础镜像也称为父镜像，将镜像从远程存储库提取到本地时，仅仅只下载本地计算机上尚未存在的层， Docker通过重用现有层来节省空间和时间。

Dockerfile指令是一行开头的大写单词，后紧跟其参数，Dockerfile中的每一行都可以包含一条指令。构建图像时，将从上到下处理指令，如下：

只有FROM，RUN，COPY和ADD指令才能在最终镜像中创建镜像层，其他指令只是作为配置或说明，比如添加元数据或告诉Docker在运行时执行某些操作，例如公开端口或运行命令。在本文中，我们使用基于linux的Docker镜像，当然我们也可以使用基于Windows的镜像，建议使用linux。接下来我们来过滤下Dockerfile中各个指令说明。

Dockerfile指令

FROM - 指定基础（父）镜像。

LABEL - 提供元数据，包含维护者信息。

ENV - 设置持久化环境变量。

RUN - 运行命令并创建镜像层，用于将包安装到容器中。

COPY - 将文件和目录复制到容器中。

ADD - 将文件和目录复制到容器中。可以upack本地.tar文件。

CMD - 为执行容器提供命令和参数，可以覆盖参数，只能有一个CMD。

WORKDIR - 设置后续说明的工作目录。

ARG - 定义一个在构建时传递给Docker的变量。

ENTRYPOINT - 为正在执行的容器提供命令和参数。 

EXPOSE - 对外暴露端口。

VOLUME - 创建目录用于访问和存储持久化数据。

.NET Core入门例子

接下来我们以.NET Core中使用Docker并输出Hello World结束本文。

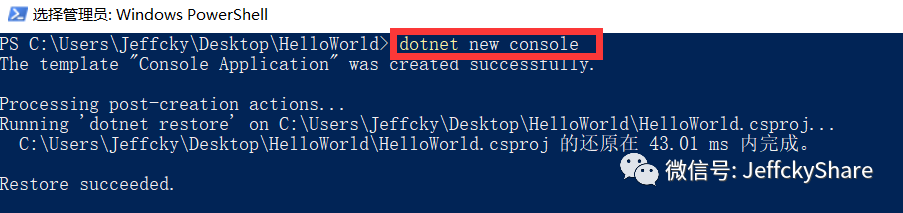
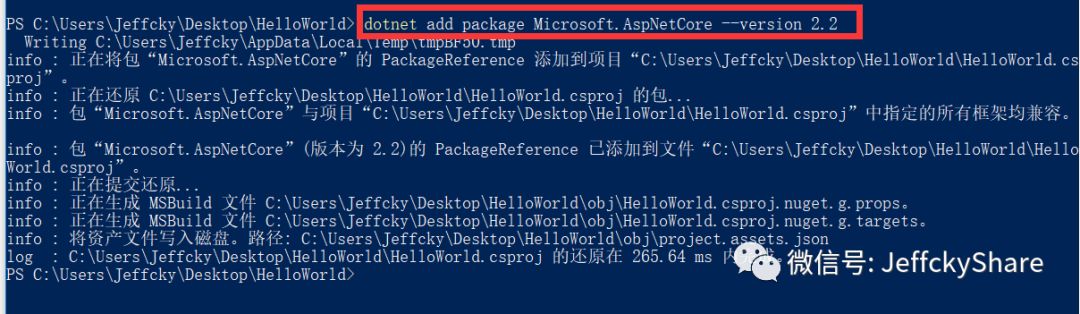
我们通过命令创建一个.NET Core控制台程序，接下来为了在页面上输出Hello World，我们需要使用中间件，所以我们添加AspNetCore包，如下：

然后我们打开控制台程序，添加中间件打印Hello World代码：

程序已就绪完毕，接下来我们发布该控制台程序，如下：

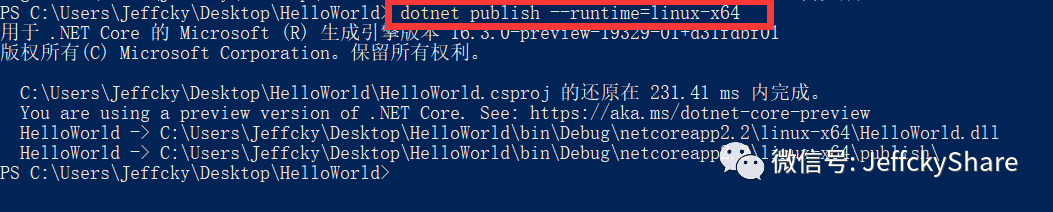
接下来将执行上述步骤生成的bin目录（实际上只需拷贝发布后生成的publish目录即可，为了省事，我直接拷贝了整个bin目录）拷贝到ubuntu中

由于我对linux不熟悉，所以采用虚拟机加载桌面端ubuntu镜像的方式，对于从未使用过linux的童鞋，推荐使用桌面端ubuntu，友好的GUI界面，方便我们初学知道各个文件夹是做什么的，一看便知，后续再使用服务端版的ubuntu就会得心应手啦。 

接下来我们进入HelloWorld文件目录，创建Dockerfile文件从而来创建.NET Core镜像。

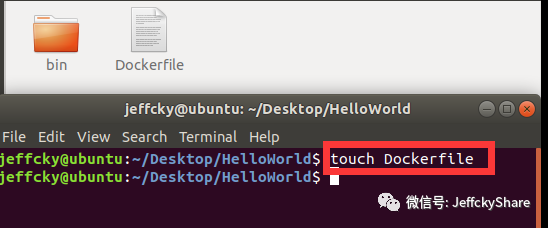
然后我们来编写Dockerfile文件构建镜像，如下：

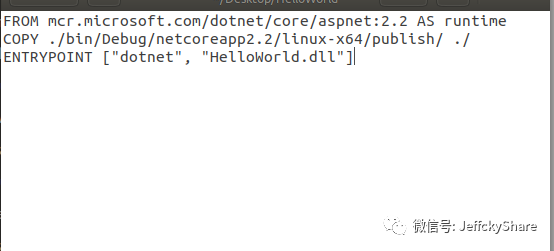
父镜像为.NET Core 2.2版本和我们创建的程序版本一致，然后将我们的应用程序(即publish目录)拷贝，最后指定程序运行的命令和参数。有了Dockerfile文件，那么我们就可以开始构建镜像了，终端继续运行如下命令(注意：镜像标签名称必须全部为小写，否则报错)：

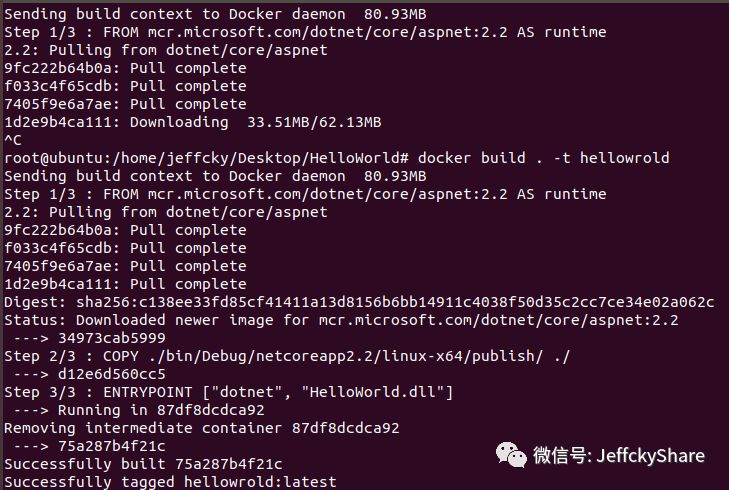
镜像已构建完毕，接下来则是创建并启动容器运行程序，如下：

从上述我们可看到容器已正常启动，且运行环境为生产环境，监听端口为5050。桌面版ubuntu默认为我们安装了火狐浏览器，此时我们打开浏览器将会输出Hello World，如下：

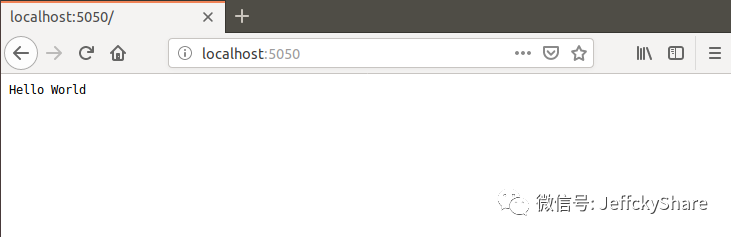
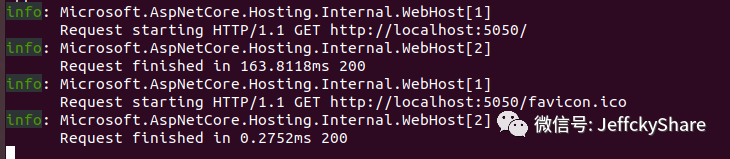
本文我们介绍Docker中的一些术语，然后最后写了一个在.NET Core中使用Docker的入门例子，非常简单。若直接使用服务端版本的ubuntu我是一脸懵逼，有了界面，我也大概知道了一些文件夹里存放的是什么，一目了然，虽说这还只是冰山一角，每天积累一点，日积月累，厚积薄发嘛不是。