http://blog.csdn.net/Andrewseu/article/details/46991541

本讲大纲：

1.最优间隔分类器(optimal margin classifier) 
2.原始/对偶优化问题（KKT）（primal/dual optimization problem） 
3.SVM对偶(SVM dual) 
4.核方法(kernels)(简要，下一讲详细)

1.最优间隔分类器

假设给我们的数据集是线性可分的(linearly separable). 就是说用超平面可以分隔正负样本. 我们要找到最大的几何间隔. 我们可以转化为下面的优化问题： 
 
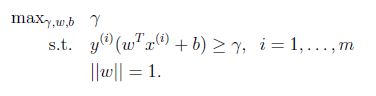
由于||W|| = 1，这保证了函数间隔等于几何间隔，只要解决了上面的优化问题我们就解决了这个问题，但是||W||是一个不好的（非凸性）的限制，这不是我们能够直接用软件解决的优化问题. 因此转化为更好的一个问题： 

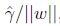
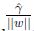
我们最大化, 我们把限制||W||去掉了，但是仍然是非凸性的.

前面有讨论过对w和b加上任意比例的限制不会改变什么. 因此，加上规模的限制，对训练集的函数间隔设置为1：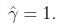 
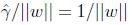
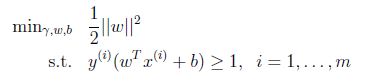
因此，最优化问题变为： 
 
上面的优化问题变为一个凸二次目标函数(convex quadratic objective). 这给我们一个最优间隔分类器的解决方案. 这个优化问题可以用商用的二次编程代码解决.

2.原始/对偶优化问题

2.1 拉格朗日二元性(Lagrange duality) 
考虑下面形式的问题： 
 
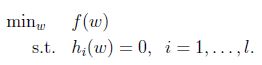
我们可以用拉格朗日乘数法来解决这个问题.

定义Lagrangian为： 
 
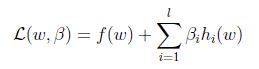
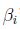
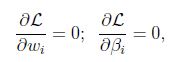
这边成为拉格朗日乘数（Lagrange multipliers）. 另其偏导数为零. 
 
然后解出w和

2.2 原始优化问题（primal optimization problem） 
 
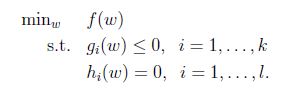
定义一般的拉格朗日算子（generalized Lagrangian）: 
 
是拉格朗日乘数. 
 
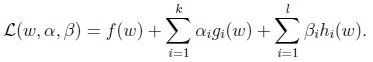
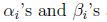
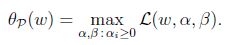
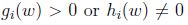
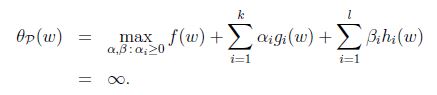
下标”P”表示”prime”, 如果给定的w违反了原始限制（），则 
 
如果w满足原始限制，那么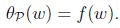 因此： 

考虑最小化问题： 
 
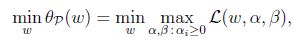
可以看到回到了最初的原始问题. 定义目标的原始值为.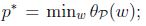

一个略微不同的问题： 
 
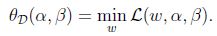
下标”D”表示”dual”.

2.3 对偶优化问题(dual optimization problem) 
 
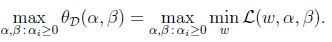
同样的，定义目标的对偶值为：

显然：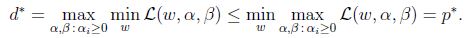 
（函数最小值的最大值肯定小于等于最大值的最小值），在某些条件下，会有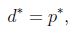，因此我们可以通过解决原始问题来解决对偶问题.

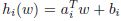
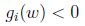
假设f和g是凸函数（黑塞矩阵为半正定的），h为仿射函数(affine，和线性是一样的，只不过是加了截距，). 假设g是严格可行的，就是说对于所有的i存在.

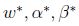
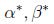
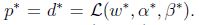
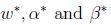
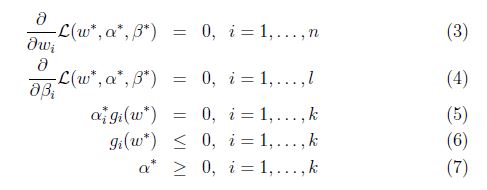
基于上面的假设，肯定存在使得w*是原始问题的解而是对偶问题的解. 而且，满足KKT条件（Karush-Kuhn-Tucker condition）,如下： 
 
如果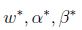满足KKT条件，那么就是原始问题和对偶问题的解. 
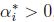
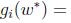
等式（5）称为KKT对偶补充条件（KKT dual complementarity condition）. 具体来说，就是如果，那么0.

3.SVM对偶

前面为了找到最优间隔分类器，提到以下的优化问题（原始优化）： 
 
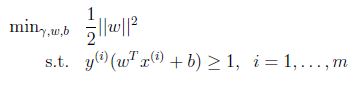
限制可以写为： 
 
 
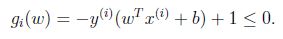
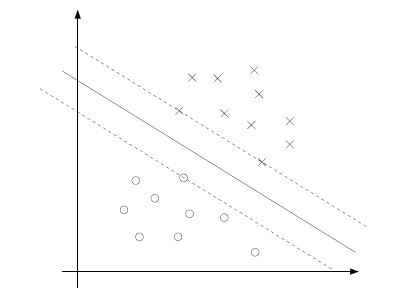
（实线为超平面） 
最小的间隔是离决定边界最近的点，上图中有三个（一个负的两个正的），因此对于我们的优化问题只有三个a是不等于零的. (KKT对偶补充条件，只有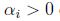，函数边界才等于 1). 这三个点被称为支持向量（support vector）. 支持向量的数量比训练样本数量小很多在以后会非常有用.

为优化问题构建Lagrangian，有： 
 
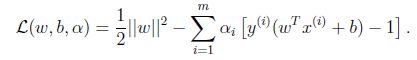
对w求偏导： 
 
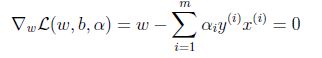
推出： 
 
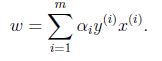
对b求偏导： 

根据上面的式子化简得到： 
 
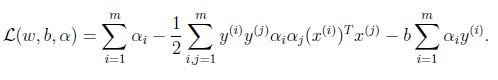
最后一项为零，进一步得到： 

得到以下对偶优化问题： 
 
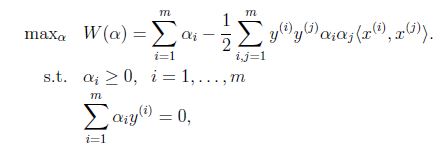
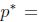
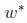
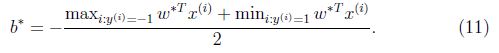
需要满足d*和KKT条件来满足我们的优化问题. 因此我们可以通过解决原始问题来解决对偶问题. 原始w作为a的函数，已经有了之后, 很容易得到截距b为： 
 
再得到： 
 
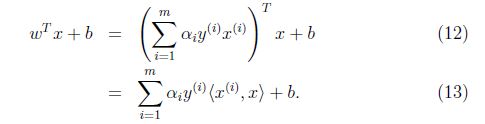
因此如果我们找到了a，为了预测，我们只需要计算x和数据集中点的内积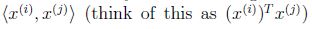（）. 并且我们知道除了支持向量a都是零，因此我们只需要计算x和支持向量的内积就可以进行预测了.

4.核方法

有时候训练样本的维数很高，甚至有可能得到的特征向量是无限维的. 通过计算不同方法的内积，利用内积来进行有效的预测.
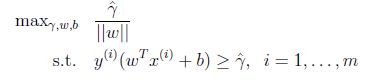
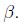
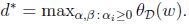
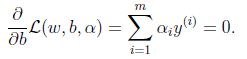
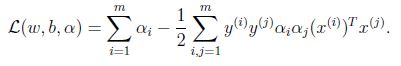