题目描述
班里N个小朋友，每个人都有自己最崇拜的一个小朋友（也可以是自己）。
在一个游戏中，需要小朋友坐一个圈，
每个小朋友都有自己最崇拜的小朋友在他的右手边。
求满足条件的圈最大多少人？
小朋友编号为1,2,3,…N
输入
输入第一行，一个整数N（3<N<100000）
接下来一行N个整数，由空格分开。表示每位小朋友崇拜的小朋友的编号。
输出
输出一个整数，表示满足条件的最大圈的人数。
样例输入
9
3 4 2 5 3 8 4 6 9
样例输出
4
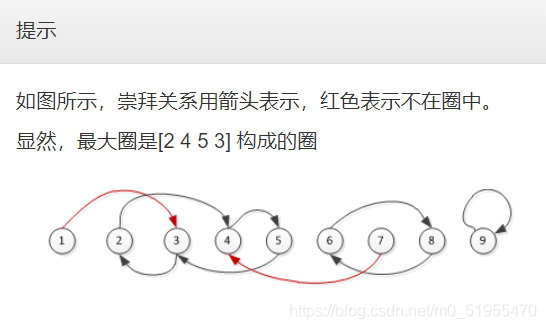
解题思路：
题意大意:n条有向边，找出最大环。
我们发现，如果一个小朋友没有被任何人崇拜,那么他一定不位于环中。为此我们可以设置一个indug数组预处理。如果2被崇拜了那么indug[2]就加加，那么后续我们只需要dfs不为0的小朋友即可。
优化
可是遍历小朋友的话会有大量重复。比如1->3->5->1，我们遍历了1，那么其实3和5是不需要去管的对吧。所以就有了代码。
————————————————
思路转载链接：https://blog.csdn.net/jziwjxjd/article/details/104154260
代码如下：
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
bool st[N];
int debug[N];
int cnt;
int maxv;void dfs(int head, int dian, int len) {if (a[head] == dian) {maxv = max(len, maxv);return ;}st[a[head]] = true;dfs(a[head], dian, len + 1);
}int main() {ios::sync_with_stdio(false);cin.tie(0);int n;cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];debug[a[i]]++;}for (int i = 1; i <= n; i++) {if (debug[i] != 0 && !st[i]) {st[i] = true;dfs(i, i, 1);}}cout << maxv << endl;return 0;
}
