
在数据的预处理阶段,特征提取和数据降维是提升模型表示能力的一种重要手段。
特征提取主要是从数据中找到有用的特征,用于提升模型的表示能力,而数据降维主要是在不减少模型准确率的情况下减少数据的特征数量。
比如,我们要搭建一个预测身高的模型,现有的数据包括身高、性别、年龄、饭量以及是否喜欢运动,这么多的变量如何确定模型呢?
这就要用到数据降维。简单说就是把性别、年龄、饭量、是否喜欢运动组成的四维变量转换为一维,再寻找与身高之间的关系就方便多了。
那四维变量如何变为一维呢?
从原理上来说,将不同变量按照不同权重转化到一维空间,再将各个变量叠加就组成一个新的一维变量。
从方法上来说,下面将主要介绍的3种方法——主成分分析、核主成分分析和ISomap流行学习都能实现数据降维。
其中,主成分分析(PCA)和核主成分分析(KPCA)将应用于人脸数据集特征提取,ISomap流形学习将应用在手写数字数据集上。
一、主成分分析(PCA)
主成分分析是一种分析、简化数据集、提取主要成分的技术。
在实际生活中,特征之间可能存在一定的相关性,比如上文中的年龄和饭量,这种情况下就存在重叠的信息。
主成分分析则可以通过少数的特征来保留原始数据集中的大部分信息,从而减少数据维度。
具体原理可以参考文章:
主成分分析(PCA)原理详解_李春春的专栏-CSDN博客_主成分分析blog.csdn.net
当然,主成分分析也有缺点,其分析效果主要依赖于给定的数据集,所以数据集的准确性对分析结果影响很大。
下面我们将以AR人脸数据集(没有数据集的小伙伴可以私信我或在评论区留言)为例,使用PCA技术找到数据集中的特征脸数据。
AR人脸数据集有100类人脸,其中男、女各50类,每类数据有26幅图像,每幅图像大小为165*120。第一步要做的就是载入相关方法和数据:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = "retina"
from matplotlib.font_manager import FontProperties
fonts = FontProperties(fname="C:WindowsFontsSimHei.ttf", size=14)
from sklearn.decomposition import PCA
import cv2
from sklearn.preprocessing import StandardScalerface = []
label = []
for i in ["m","w"]:for m in range(1,51):for n in range(1,27):path='D:/AR/'+i+"-"+str(m).rjust(3,"0")+"-"+str(n).rjust(2,"0")+'.pgm' #每个人文件位置不同img=cv2.imread(path,cv2.IMREAD_GRAYSCALE)h,w=img.shapeimg_col=img.reshape(h*w)face.append(img_col)face_trans = []
face = np.array(face).T
face.shape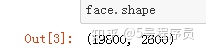
从数据组成可以看出,该数据集共有2600个人脸图像,每个图像的特征维度为19800维。
上述代码还使用了OpenCV(需要用pip安装)导入图片,函数cv2.imread(filepath,flags)可以读入一副图片,其中filepath为要读入图片的完整路径,flags为读入图片的标志,cv2.IMREAD_COLOR为默认参数,指读入一副彩色图片但忽略alpha通道,cv2.IMREAD_GRAYSCALE指读入灰度图片。
“.T”表示将数组反转,如果不进行反转将会得到(2600, 19800)的数组,在做特征提取时将会对单张图片进行降维(也就是对19800进行降维),并不是我们想要的结果。
np.array(face).T也可以用下面的代码替代,结果是一样的:
for x in range(len(face[0])):temp = []for y in range(len(face)):temp.append(face[y][x])face_trans.append(temp)
face = np.array(face_trans)完成数据载入后就能查看导入的图像了:
height = 165
width = 120
plt.figure(figsize=(10,6))
for ii in np.arange(10):plt.subplot(2,5,ii+1)image = face[:,ii*26].reshape(height,width)vmax = max(image.max(),-image.min())plt.imshow(image,cmap=plt.cm.gray,interpolation='nearest',vmin=-vmax,vmax=vmax)plt.axis("off")
plt.subplots_adjust(wspace=0.1,hspace=0.1)
plt.show() height和width是图片的长和宽,plt.imshow()函数可以实现热图绘制,参数plt.cm.gray表示返回灰度色图,interpolation='nearest'指线性图,一般由RGB组成的图都设置为线性,vmin和vmax参数可以控制非线性缩放。
plt.subplots_adjust()用来控制子图布局,wspace、hspace分别表示子图之间左右、上下的间距。

下面对每张图像进行标准化处理:
sc = StandardScaler()
face = sc.fit_transform(face)
face
标准化后对数据集的几张图像进行可视化并查看数据集内容,相比标准化前颜色稍浅:
height = 165
width = 120
plt.figure(figsize=(10,6))
for ii in np.arange(10):plt.subplot(2,5,ii+1)image = face[:,ii*26].reshape(height,width)vmax = max(image.max(),-image.min())plt.imshow(image,cmap=plt.cm.gray,interpolation='nearest',vmin=-vmax,vmax=vmax)plt.axis("off")
plt.subplots_adjust(wspace=0.1,hspace=0.1)
plt.show()AR人脸图像如图所示:

接下来使用主成分分析法找到数据集中的100张特征脸数据并计算数据集解释方差百分比:
pca = PCA(n_components=100,svd_solver="randomized",whiten=True)
face_pca = pca.fit_transform(face)
np.sum(pca.explained_variance_ratio_)PCA函数中的n_components参数指需要保持的主成分个数,svd_solver指定求解时使用的算法,whiten表示是否对数据集进行白化处理。
运行后可以看到如下结果:

可以发现得到的100张特征人脸数据达到了93.73%的解释方差,保留了数据集中的大部分信息。
再次查看降维后的特征脸图像:
height = 165
width = 120
plt.figure(figsize=(10,6))
for ii in np.arange(10):plt.subplot(2,5,ii+1)image = face_pca[:,ii].reshape(height,width)vmax = max(image.max(),-image.min())plt.imshow(image,cmap=plt.cm.gray,interpolation='nearest',vmin=-vmax,vmax=vmax)plt.axis("off")
plt.subplots_adjust(wspace=0.1,hspace=0.1)
plt.show()PCA得到的特征脸如图所示:

可以看出,大部分特征脸都是带有眼镜的,说明原始数据中含有大量的带有眼镜的人脸数据。
二、核主成分分析(KPCA)
PCA是一种线性的数据降维技术,而核主成分分析(KPCA)则可以得到数据的非线性表示。
简单理解就是,KPCA是PCA的升级版,通过只保留前面的主要特征来达到对数据进行降维的目的。
具体原理可以参考文章:
解释一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推导过程~blog.csdn.net
核主成分分析的“核”,事实上是加入了核函数,用核函数替代原始数据让分析更加准确。
下面使用KernelPCA函数对AR数据集提取特征脸数据:
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components=100,kernel="rbf")
face_kpca = kpca.fit_transform(face)height = 165
width = 120
plt.figure(figsize=(10,6))
for ii in np.arange(10):plt.subplot(2,5,ii+1)image = face_kpca[:,ii].reshape(height,width)vmax = max(image.max(),-image.min())plt.imshow(image,cmap=plt.cm.gray,interpolation='nearest',vmin=-vmax,vmax=vmax)plt.axis("off")
plt.subplots_adjust(wspace=0.1,hspace=0.1)
plt.show()注意:KernelPCA函数对内存要求较高,很可能出现MemoryError,建议运行内存在8G及以上。
KernelPCA函数中的n_components参数与PCA相同,表示需要保持的主成分个数。
Kernel表示核方法,可以为“linear”“poly”“rbf”“sigmoid”“cosine”“precomputed”。
KernelPCA得到的特征脸如图所示:

与PCA得到的特征脸相比,核主成分分析的轮廓更加鲜明。
从上面的示例可以看出,无论是PCA还是KPCA都是通过对数据样本量进行降维得到特征脸,降维还可以作用于数据的特征维度。
如果再对降维后的数据进行数据可视化,能够更方便地分析数据之间的结构和关系。
下面使用核主成分分析对人脸数据集进行特征提取,然后可视化,并分析原始图像之间的关系:
faceT = face.T
kpca_f = KernelPCA(n_components=100,kernel="rbf")
kpca_f.fit(faceT)
face_kpcaf = kpca_f.transform(faceT)
face_kpcaf.shape反转后将19800维降维:

图片可视化:
from matplotlib import offsetbox
plt.figure(figsize=(16,12))
ax = plt.subplot(111)
x = face_kpcaf[:,0]
y = face_kpcaf[:,1]
images = []
for i in range(len(x)):x0,y0 = x[i],y[i]img = np.reshape(faceT[i,:],(165,120))image = offsetbox.OffsetImage(img,zoom=0.4)ab = offsetbox.AnnotationBbox(image,(x0,y0),xycoords='data',frameon=False)images.append(ax.add_artist(ab))
ax.update_datalim(np.column_stack([x,y]))
ax.autoscale()
plt.xlabel("KernelPCA主成分1",FontProperties=fonts)
plt.ylabel("KernelPCA主成分2",FontProperties=fonts)
plt.show()代码中使用offsetbox包绘制图片,offsetbox.OffsetImage()为获取图片方法,参数zoom表示缩放比例,offsetbox.AnnotationBbox()为设定图片坐标方法,参数frameon表示是否加外框。
KPCA下的空间结构如图所示:
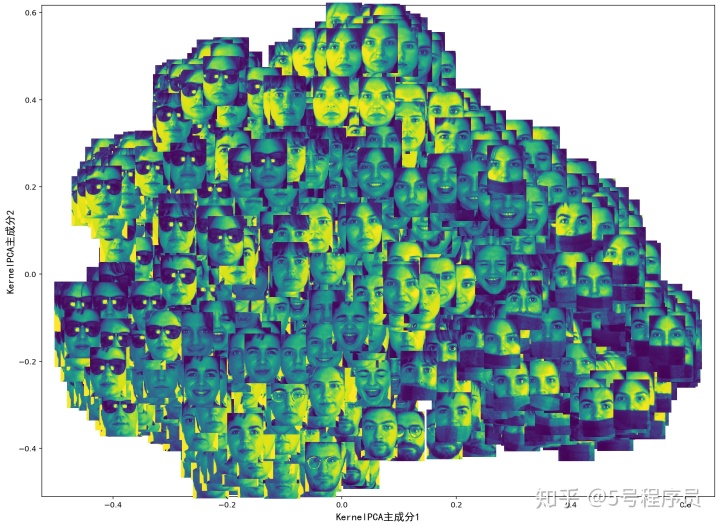
上面的程序中,相应坐标的位置就是核主成分的前两个主成分,分别为X轴和Y轴,然后将2600张图片绘制到图像上。
从图上可以发现,原始数据图像在核主成分空间中的分布特点是:在X轴从左到右分布,依次为戴墨镜图像、干净的人脸图像、戴围巾图像。
在Y轴从上到下分布,也是呈区域性分布。
三、Isomap流形学习
Isomap流形学习是借鉴了拓扑流形概念的一种降维方法,可以用于数据降维。
流形并不是一个“形状”,而是一个“空间”。
其原理可以简单理解为通过近邻的距离来计算高维空间中样本点的距离。
具体原理可以参考文章:
流形学习之等距特征映射(Isomap)_长夜悠悠的博客-CSDN博客blog.csdn.net
下面用手写字体数据集进行演示:
from sklearn.manifold import Isomap
from sklearn.datasets import load_digits
X,Y = load_digits(return_X_y=True)
X = X[0:1000,:]
Y = Y[0:1000]查看手写字体数据集:
size = 8
plt.figure(figsize=(10,4))
for ii in np.arange(10):plt.subplot(2,5,ii+1)image = X[ii,:].reshape(size,size)plt.imshow(image,interpolation='nearest')plt.axis("off")
plt.subplots_adjust(wspace=0.1,hspace=0.1)
plt.show()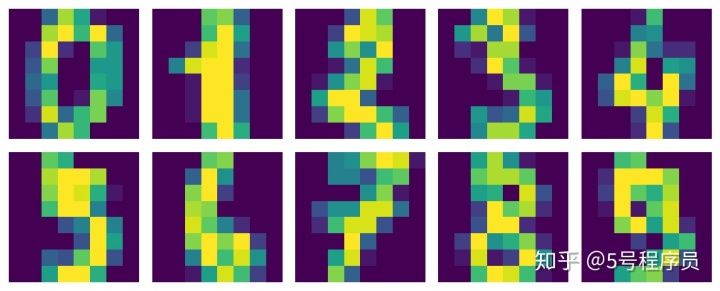
从sklearn.datasets库中使用load_digits函数可以导入手写字体数据集,并使用sklearn库中的manifold模块的Isomap函数对手写字体数据集进行降维学习:
n_neighbors = [5,10,15,20]
shape = ["s","p","*","h","+","x","D","o","v",">"]
for n in n_neighbors:isomap = Isomap(n_neighbors=n,n_components=2)im_iso = isomap.fit_transform(X)plt.figure(figsize=(10,7))for ii in range(len(np.unique(Y))):scatter = im_iso[Y==ii,:]plt.scatter(scatter[:,0],scatter[:,1],color=plt.cm.Set1(ii/10.),marker=shape[ii],label=str(ii))plt.legend()plt.title("Isnmap根据"+str(n)+"个近邻得到的降维",FontProperties=fonts)plt.legend()plt.show()分别根据不同的近邻数目[5,10,15,20]来计算流形降维结果如下:
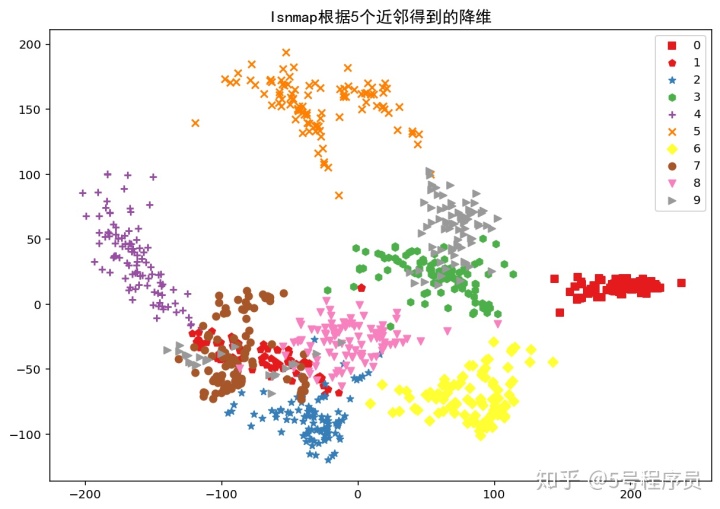
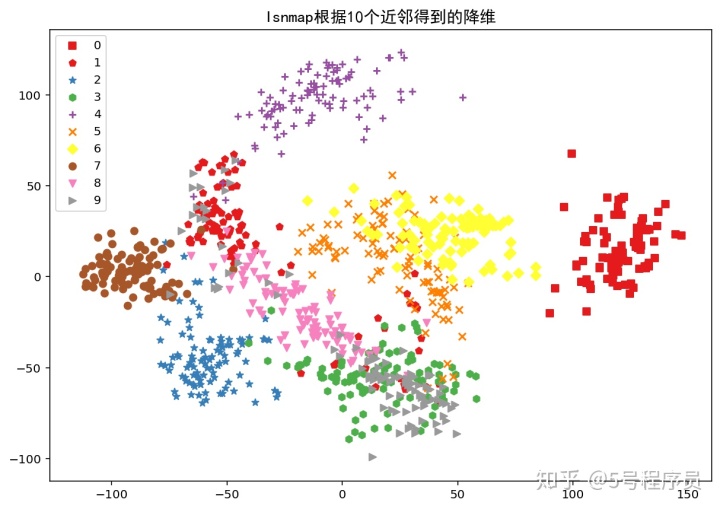
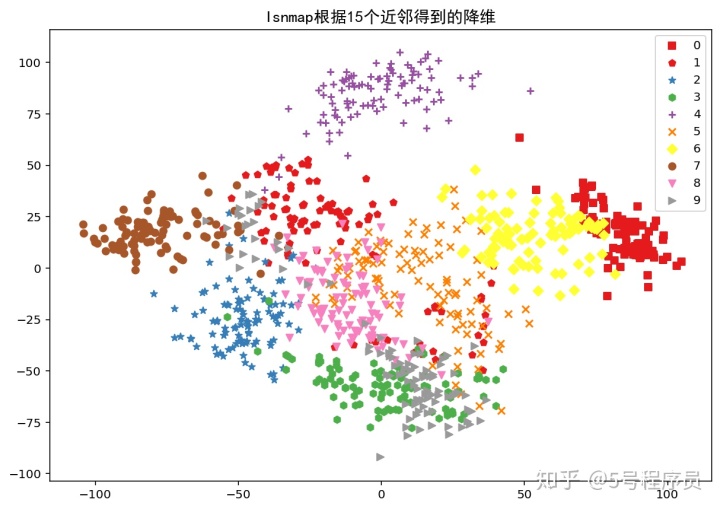
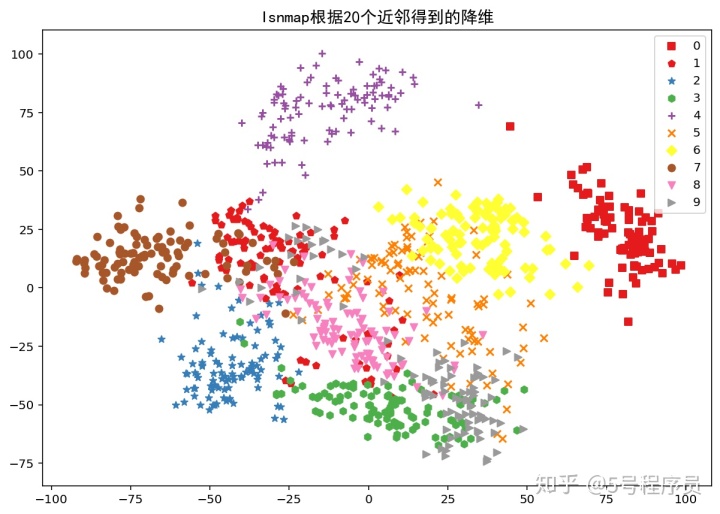
从图中可以看出,近邻数量越多,降维后数据之间就越紧密,就越不能很好地区分数据。
因此,近邻的个数对流形降维得到的结果影响很大,在建立分类模型前需要留意近邻数量对最终结果的影响。
数据提取和降维是数据分析中非常重要的部分,随着大数据到来,数据的海量增加使得高维数据在今后越来越常见,如何提取和降维就显得格外重要。
关于特征提取和降维的内容就这么多,理解起来有一定困难,特别是PCA方法的理解,在今后的学习中也会用到,需要牢牢掌握。
数据预处理到此就结束了,还想增长技能的小伙伴可以再查查相关资料。下一次我们将开始一个新的模块——模型训练和评估。
你确定不关注我一波?!









_谷歌发布Flutter Alpha:支持Windows)


--学习笔记(下))



不同数字的思考)


![[蓝桥杯2017初赛]贪吃蛇长度-模拟(水题)](http://pic.xiahunao.cn/[蓝桥杯2017初赛]贪吃蛇长度-模拟(水题))
转储设置,看本文就够了!)