前段时间开发新的微信小程序,借此机会将老掉牙的支付模块重构,并且支持现金支付(之前都是虚拟币支付),在重构期间遇到计算上的一些精度问题,虽然数额影响非常小但是影响比较大,我觉得有必要总结以下遇到的一些问题,并且解决弄清楚他的原来,因此有下文。 当我们程序中涉及到一些double或者float类型的数据,并且精度要求比较高,小数点位数比较多的时候,可能会出现一些非常奇葩的问题,我下面针对遇到的一些问题给出几个说明案例:
System . out. println ( 1f == 0.9999999f ) ;
System . out. println ( 1f == 0.99999999f ) ;
float f = 0.6f ;
double d1 = 0.6d ;
double d2 = f;
System . out. println ( ( d1 == d2) + " " + f + " " + d2) ;
System . out. println ( 0.2 + 0.7 ) ;
float f1 = 8455263f ; for ( int i = 0 ; i < 10 ; i++ ) { System . out. println ( f1) ; f1++ ; }
float f2 = 84552631f ; for ( int i = 0 ; i < 10 ; i++ ) { System . out. println ( f2) ; f2++ ; }
要搞清除还是得从java的double和float类型来入手,我们都知道,计算机只认识二进制的0,1,那么在double和float中有整数部分,小数部分,如此说来那么应该会有一定的方式将小数转为计算机认识的0,1 组合,这中方法是定义的一个转换标准,其实而Java中浮点数采用的是IEEE 754标准 IEEE 745 是IEEE二进制浮点数算数标准(Standard for Floating-Point Arthmetic)的标准编号,等同一个国际标准ISO之类,是美国哪家公司订的,这个标准定义来表示浮点数的格式(包括负零-0)与反常值(denormal number),一些特殊数值(例如无穷inf,非数值NaN)以及一些数值的“浮点数运算子”它知名来四种数值修约规则和五种例外状况。还有要了解的可以去JDK官网 我们学习计算机组成原理的时候,应该学过的,Java中表示小数的时候有三个组成部分: 这三个纬度的信息,一个浮点数表示就可以完全确认下来,如下图所示的存储结构 符号位部分 S: 0 表示正数, 1 表示负数 阶码部分E (只整数部分): 对于float型浮点数,指数部分8 位,考虑可正负,因此可以表示的指数范围是-127~128 对于double类型浮点数,指数部分11 为,可正负,因此可以表示的指数范围是-1203~1024 尾数部分 M: 对于float类型来说,尾数23 为,计算成十进制就是223 = 8388608,所以十进制精度只有6~7位 对于double类型来说,尾数部分52位,计算成十进制就是252 =4503599627370496,所以十进制的精度是15~16位 以上几个都是官方的数据 浮点数float和double在内存中是按照科学计数法来存储的,取值范围是由指数的位数来决定的,精度是由尾数的位数来决定的。 浮点数 精度/位数 符号S 指数E 扩展范围 (指数的取值范围) 最大/小值(取值范围) 尾数位M 尾数取值范围(精度) float 32bit 单精度 1bit(0正1负) 8bit -27 ~ 27 -1(-128~127) 2127 (1038 级别的数) 23bit 8388608,7位,精度为6~7位 double 64bit双精度 1bit(0正1负) 11bits -210 ~ 210 -1(-1024~1023) 21023 (10308 级别的数) 52bit 45035_99627_37049_6,16位,精度为15~16位
计算过程,小数部分,将小数部分乘以2,取出结果中整数部分作为二进制表示的第一位(大于等于1为1,小于1 为0),然后在将小数部分乘以2,得到整数部分作为二进制表示第二位…依次类推知道小数部分位0. 特殊情况永远都不会位0:小数部分循环出现,无法停止,则用优先的二进制位无法表示这个小数,这也是在编程语言中小数位出现误差的原因。 我们用如下的案例来说明这个过程10.6: 0.6 * 2 = 1.2 -- -- 1
0.2 * 2 = 0.4 -- -- 0
0.4 * 2 = 0.8 -- -- 0
0.8 * 2 = 1.6 -- -- 1
0.6 * 2 = 1.2 -- -- 1
0.2 * 2 = 0.4 -- -- 0
.
.
.
0.6 * 2 = 1.2 -- -- 1
0.2 * 2 = 0.4 -- -- 0
以上我们可以发现0.6 是一个无法精确表示的一个数值,用二进制表示1001 1001 1001 1001 … 那10.6 的二进制我们可以表示如下:1010.1001 1001 1001 … 计算过程:从左到右,v[i]*2(-i) , i为从左到右的index,v[i]为该位的值,直接看例子如下: 10.6 的二进制1010.1001 1001 1001,从小数点位为基准如下: 0 * 20 + 1 * 21 + 0 * 2 2 + 1 * 23 = 0+2+0+8//(整数部分) 1 * 2-1 + 0 * 2-2 + 0 * 2-3 + 1 * 2-4 + 1 * 2-5 + 0 * 2-6 + 0 * 2-7 + 1 * 2-8 … = 0.5+0.0625 + 0.03125 ≈ 0.6 // 小数部分 我们通过开始的案例,还有之前关于double,float这部分的分析,我们来解答一下最开始的哪些问题是怎么出现的: 因为float的尾数23为,double尾数52位,所以float类型中保存的0.6 的二进制转成double二进制的时候低位的二进制自动变成0 ,与用double类型保存的0.6的二进制是不一样的,所以出问题来,如下图来解释: float 类型的0.6f:
1001 1001 1001 1001 1001 100
double类型的d1 = 0.6d:
1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001
将float类型f 赋值给double类型的d2后,d2 的实际数据位:
1001 1001 1001 1001 1001 1000 0000 0000 0000 0000 0000 0000 0000
System . out. println ( 1f == 0.99999999f ) ;
这个结果是true因为计算机无法区分这个两个的二进制数,我们也来推到一些他们的二进制表示 1.0 (十进制)↓
00111111 10000000 00000000 00000000 (二进制)↓
0x3F800000 (十六进制)0.99999999 (十进制)↓
00111111 10000000 00000000 00000000 (二进制)↓
0x3F800000 (十六进制)0.9999999 (十进制)↓
00111111 01111111 11111111 11111110 (二进制)↓
0x3F7FFFFE (十六进制)
如上,这第一个和第二个二进制数是一样的,第三个是不一样的,只是因为上面的0.99999999f(8个9) 明显超过来float类型的精度范围凑巧和1 是一样的就出现这种问题。 Java当中默认声明的小数是double类型的,其默认后缀"d"或"D"可以省略,如果要声明为float类型,需显示添加后缀"f"或"F" 我们尽量用BigDecial来计算 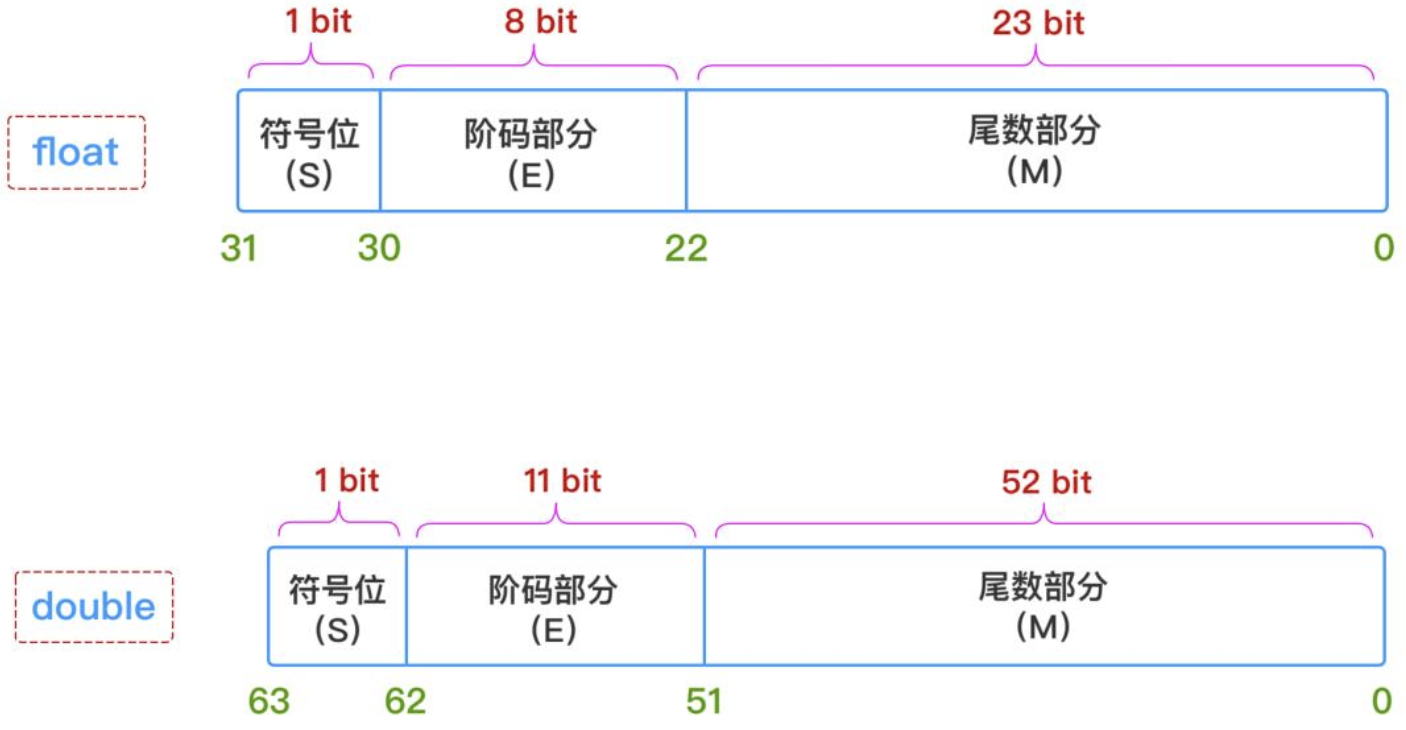

![[Qt入门]QTableWidget控件创建](http://pic.xiahunao.cn/[Qt入门]QTableWidget控件创建)


)



![[剑指offer]面试题1:赋值运算符函数](http://pic.xiahunao.cn/[剑指offer]面试题1:赋值运算符函数)


![[剑指offer]面试题3:二维数组中的查找](http://pic.xiahunao.cn/[剑指offer]面试题3:二维数组中的查找)



![[剑指offer]面试题4:替换空格](http://pic.xiahunao.cn/[剑指offer]面试题4:替换空格)

![[剑指offer]面试题5:从尾到头打印链表](http://pic.xiahunao.cn/[剑指offer]面试题5:从尾到头打印链表)

