高斯积分作为一种特殊的反常积分，其应用范围相当广泛，无论是在概率论中所引入的高斯分布（亦称正态分布），还是在统计物理中的相关应用，都表明其有着至关重要的作用。

下面我们来介绍一种记忆高斯积分的方法：

01

从量纲谈起

我们之前曾借助量纲辅助记忆了不少公式，有兴趣的读者不妨在《物理记忆》栏目中回顾有关量纲分析的相关应用。但在该专栏中未曾讨论过量纲如何在超越函数中应用，现在我们做一讨论:

简单回顾正弦，余弦，e指数这三大超越函数的幂级数展开式：

从中不难看出，若x具有物理量纲，则展开式的每一项量纲都不相同，而量纲不相同的物理量是无法相加的，因此x仅能为无量纲数，例如弧度制的角度θ

我们回到高斯积分本身：

对此公式，我们不妨给x赋予长度的量纲

那么根据上述分析，a的量纲必须为长度的负二次方，方能使a乘以x平方是无量纲数。

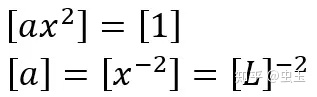
我们观察等号左侧e指数项整体无量纲，dx具有长度量纲，因此等号左侧具有长度量纲

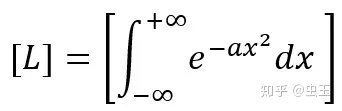
那么等号右侧也必须有长度量纲[L]

考虑到a具有长度负二次方的量纲，为使等号右侧也为长度量纲，因此等号右侧必须出现a的负二分之一次方：

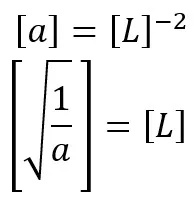
02

π何来？

第一部分已经分析了右侧必须出现a的负二分之一次方，但尚未解释为何还需要再乘以常系数根号π，为确定此系数，可以令a=1

该积分右侧便是所需确定的系数

下面采用一些技巧来计算上述积分：

由此我们转化为了二重积分，看似将问题复杂化了，实则引入了更强的对称性，我们此时可以用极坐标去处理：直角坐标的面积微元dxdy对应极坐标的面积微元rdrdθ，且积分是对整个二维平面进行积分，因此有：

最终得到：

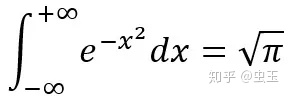
03

记忆

第二部分的过程仅仅给出了具体推导过程，而至于记忆方法，我们可以这么想：

为了计算积分结果，将本来对称性较低的积分（原来的被积函数是偶函数，仅具有轴对称型）化为根号下二重积分，以便于利用极坐标下更好的对称性，而极坐标网格是一圈一圈的圆环构成的，而π这个常数的出现恰是与圆密切联系的，因此我们可以由此记忆常数根号π的由来

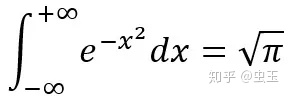
再结合第一部分，由量纲法得出等号右侧必须出现a的负二分之一次方

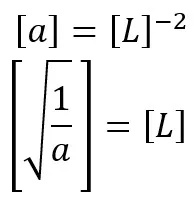
综上，结合二者便可记忆高斯积分公式：

更多巧妙记忆方法请关注公众号：数理tricks