
1.1 Supervised Learning
已知输入x以及其对应的标签y,求解 f:x→y
回归 regression:输出的结果y是一个连续的变量 y=ℝ
分类 classification:输出的结果y是一个离散的变量 y={1,2,3...,k}
分类 classification:分类到各不知名的聚类中
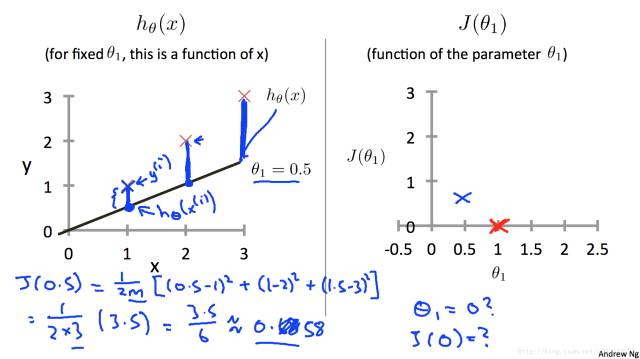
当theta1 = 0.5的时候,计算得到J(θ)=0.58
当theta1=0的时候,计算得到J(θ)≈2.3
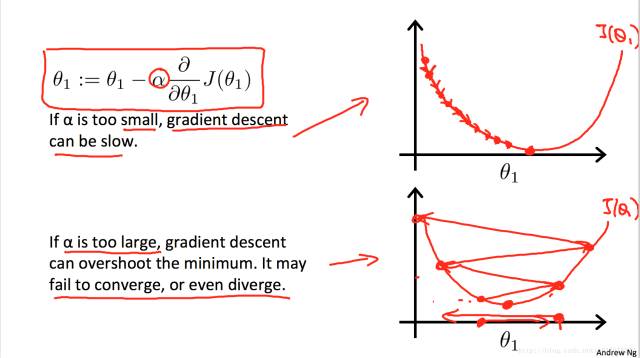
如果α取值太小,那么下降到最小值的速度会比较慢
如果α取值太大,可能一步就跳过了最小值点……
1.2 Unsupervised Learning
已知输入x,并不知道其所属的类别标签y,求解将x们划分到不同的聚类中,这些聚类具体是什么类别并不知道。
1.3 Semi-supervised Learning
输入的x中,一部分有对应的标签y,大部分没有。通过这一部分有标签的去推测各不知名的聚类是什么类别。
1.4 一张图弄懂

(图片来源:台湾大学林轩田的《机器学习基石》3-2)
2.1 Model Representation
例子:房价预测 - 给出房子的各种特征,如面积、位置等,以及该房子对应的价格。学习一个模型,当输出其他房子的特征时,能够预测出新房子的价格。
明显这是一个回归模型。
数据说明:
| (x(i), y(i)) | 训练集中的第i条数据 |
|---|---|
| x | 输入数据 |
| y | 输出数据,数据x的标签(真实输出结果) |
| x(i)j | 第i条数据的第j个特征 |
| m | 训练集中数据的个数 |
| h(x) | 学习得到的模型 |
| ŷ | 模型对输入数据x的预测结果 |
 由于一开始我们并不知道θ是多少,而这个就是模型需要通过数据学习得到的,和人学习一样,模型需要知道自己究竟哪里错了才能够进一步学习。
由于一开始我们并不知道θ是多少,而这个就是模型需要通过数据学习得到的,和人学习一样,模型需要知道自己究竟哪里错了才能够进一步学习。
于是提出模型的错误公式,loss/cost function来定义这个错误。
2.2 Cost Function
最简单的错误评估,就是将预测出来的结果同真实的结果做一个平方差:
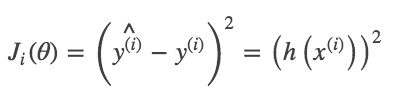
因为有m条数据,所以将这些个平方差求和之后再平均一下,作为整个训练集的error:
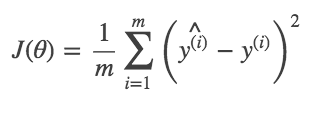
再者,为了接下来模型根据这个error进行学习的以后更加方便,再除以2(因为平方项在求导的时候可以与这个分母2抵消):
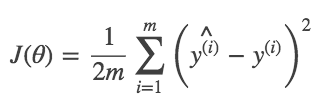
而最终的目的就是让这个error最小,只要error最小了,那就说明这个h(x)预测出来的结果和真实的结果相差不大了,那我们的模型就训练完毕了。
学习目标:

2.3 Cost Function - intuition
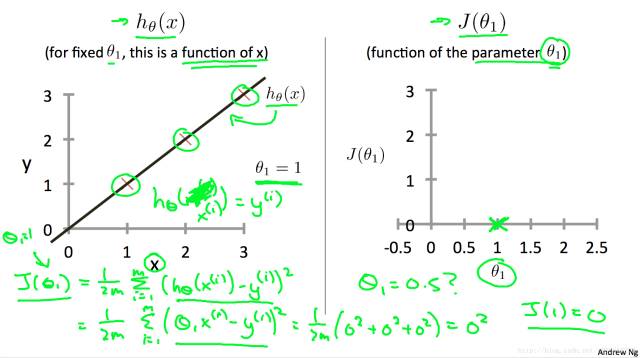
接下来通过几个例子来了解一下cost function是怎么工作的,θ又该怎么取值。
下面的图中,红色叉叉表示训练数据,黑色直线代表h(x)。
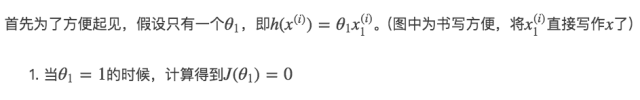

4. 以此类推,再画出一些点,然后连接起来
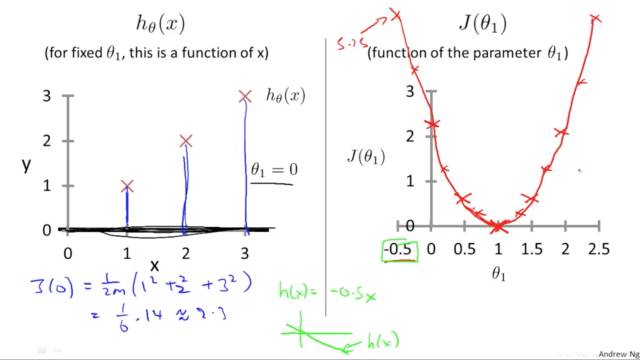


cost function取最小值的时候就是凹陷处,数学意义上梯度为0的地方。
2.4 Gradient Descent


更新过程可视化如下,从上面的点一直沿着一定的方向下降到下面的点:



下面来看看这个步长α的取值问题:
另外,如果这个J(θ)不止一个最小值点,那么当落入局部最小值(local minimun),就跳不出来了,因为梯度已经变成了0,不再更新θ了。
当不断靠近最小值的过程中,每次更新的速度也会下降,因为梯度越来越小了,如下图所示:
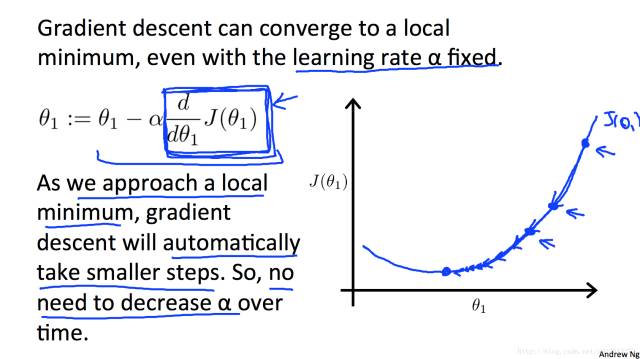
最后把gradient descent应用到linear regression with one variable问题上:

梯度求导如下;
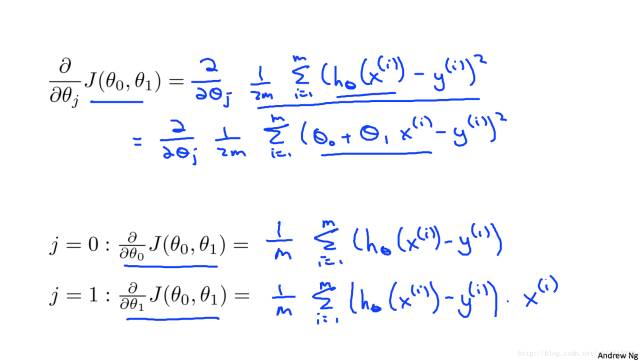
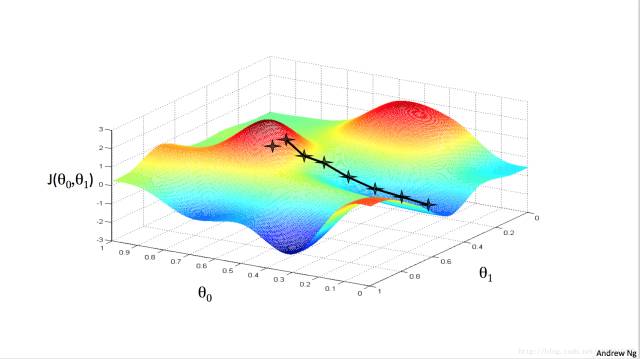
对于有一些J(θ),可能具有多个“局部最优解”,如下图:
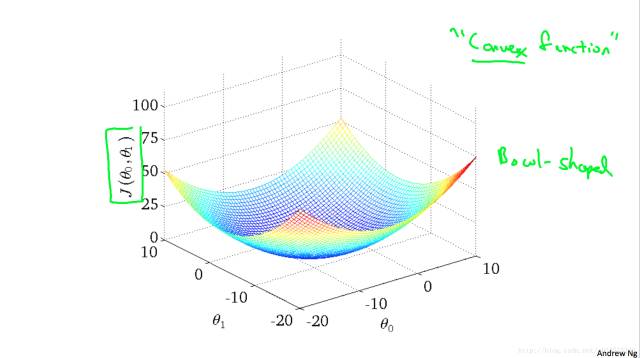
但是对于Linear Regression来说,J(θ)是“碗形”的,术语称为“convex function”,如下图:
Batch Gradient Descent
使用训练集中所有数据的error的平均值作为一次更新,即:
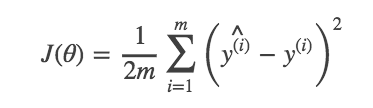
Stochastic Gradient Descent
使用训练集中的一个数据的error就更新一次,即:
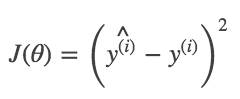
Mini-Batch Gradient Descent
使用训练集中部分数据的error的平均值作为一次更新,即:
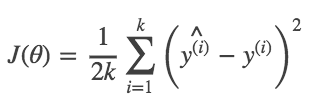




(含答案).docx...)














