文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:根据二叉树创建字符串
出处:606. 根据二叉树创建字符串
难度
3 级
题目描述
要求
给你二叉树的根结点 root \texttt{root} root,使用前序遍历的方式,将一个二叉树转换成一个由括号和整数组成的字符串,并返回。
省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例
示例 1:
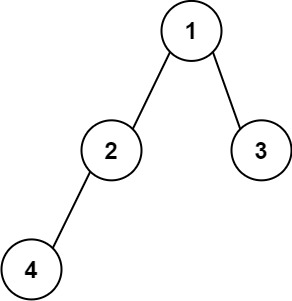
输入: root = [1,2,3,4] \texttt{root = [1,2,3,4]} root = [1,2,3,4]
输出: "1(2(4))(3)" \texttt{"1(2(4))(3)"} "1(2(4))(3)"
解释:原始字符串是 "1(2(4)())(3())" \texttt{"1(2(4)())(3())"} "1(2(4)())(3())",但是需要省略所有不必要的空括号对。结果是 "1(2(4))(3)" \texttt{"1(2(4))(3)"} "1(2(4))(3)"。
示例 2:
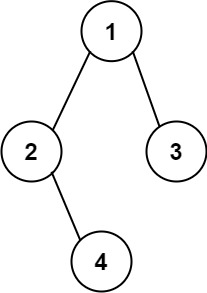
输入: root = [1,2,3,null,4] \texttt{root = [1,2,3,null,4]} root = [1,2,3,null,4]
输出: "1(2()(4))(3)" \texttt{"1(2()(4))(3)"} "1(2()(4))(3)"
解释:和第一个示例相似,除了不能省略第一个对括号来中断输入和输出之间的一对一映射关系。
数据范围
- 树中结点数目在范围 [1, 10 4 ] \texttt{[1, 10}^\texttt{4}\texttt{]} [1, 104] 内
- -1000 ≤ Node.val ≤ 1000 \texttt{-1000} \le \texttt{Node.val} \le \texttt{1000} -1000≤Node.val≤1000
解法一
思路和算法
这道题要求将二叉树按照前序遍历的顺序转换成字符串。由于二叉树的前序遍历是一个递归的过程,因此将二叉树按照前序遍历的顺序转换成字符串也可以使用递归实现。
递归的终止条件是当前结点为空,此时返回空字符串。其余情况下,首先将当前结点值拼接到字符串中,然后分别判断左子树和右子树是否为空,执行相应的操作。
-
如果左子树和右子树都为空,则当前结点是叶结点,将字符串返回。
-
如果左子树不为空且右子树为空,则对左子结点调用递归,将左子树转换成字符串并拼接到当前结点为根结点的子树对应的字符串中,左子树对应的字符串前后需要加上括号。此时不需要将右子树转换成字符串。
-
如果右子树不为空,则依次对左子结点和右子结点调用递归,将左子树和右子树分别转换成字符串并拼接到当前结点为根结点的子树对应的字符串中,左子树和右子树对应的字符串前后都需要加上括号。此时无论左子树是否为空,都需要将左子树转换成字符串。
代码
class Solution {public String tree2str(TreeNode root) {if (root == null) {return "";}StringBuffer sb = new StringBuffer();sb.append(root.val);if (root.left == null && root.right == null) {return sb.toString();}if (root.right == null) {sb.append('(');sb.append(tree2str(root.left));sb.append(')');} else {sb.append('(');sb.append(tree2str(root.left));sb.append(')');sb.append('(');sb.append(tree2str(root.right));sb.append(')');}return sb.toString();}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次,每个结点转换成字符串的时间都是 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间和转换成的字符串空间,递归调用的栈空间取决于二叉树的高度,最坏情况下是 O ( n ) O(n) O(n),字符串空间取决于结点数,是 O ( n ) O(n) O(n)。
解法二
思路和算法
也可以使用迭代的方法将二叉树转换成字符串。使用迭代的方法,需要使用栈存储结点。
由于将二叉树转换成字符串需要遵循前序遍历的顺序,因此可以按照前序遍历的方法实现。字符串中,除了每个结点值以外,还需要在正确的位置添加括号。对于左括号,只需要在每个结点值的前面添加左括号即可。更复杂的是另外两种情况:一是当左子结点为空时需要添加空括号对,二是当结点访问结束时如何添加右括号。
对于第一种情况,在访问一个结点之后,如果发现该结点的左子结点为空且右子结点不为空,则需要添加空括号对。
对于第二种情况,需要考虑括号的作用。左括号表示进入更深的一层,右括号表示回到上一层,因此在判断如何添加右括号时,应考虑当前访问的结点和下一个待访问的结点之间的层数之差。为了实现这一点,需要对每个结点维护层数,因此需要使用另一个栈存储每个结点的层数。规定根结点的层数是 0 0 0,对于存在父结点和子结点关系的两个结点,子结点的深度是父结点的深度加 1 1 1。
根据前序遍历的迭代实现,每次访问一个结点之后将当前结点移动到其左子结点,直到当前结点为空。此时将一个结点出栈,如果出栈结点的右子结点不为空,则出栈结点的右子结点即为下一个待访问的结点,如果出栈结点的右子结点为空,则继续将一个结点出栈,重复上述操作。因此当前层数(即上一个访问的左子结点的层数)和出栈结点的层数之差即为需要添加的右括号数量,添加右括号的同时将当前层数相应减少,直到当前层数等于出栈结点的层数。
遍历结束之后,层数需要恢复到访问根结点之前。由于根结点的层数是 0 0 0,因此需要添加的右括号数量为当前层数加 1 1 1。
添加最后的右括号之后,整个字符串的最外层是一对括号,包围整个二叉树转换成的字符串。由于返回值的要求是没有最外层的一对括号,因此去掉最外层的一对括号即可得到二叉树转换成的字符串。
代码
class Solution {public String tree2str(TreeNode root) {StringBuffer sb = new StringBuffer();Deque<TreeNode> nodeStack = new ArrayDeque<TreeNode>();Deque<Integer> levelStack = new ArrayDeque<Integer>();TreeNode node = root;int level = -1;int rightCount = 0;while (!nodeStack.isEmpty() || node != null) {while (node != null) {level++;sb.append('(');sb.append(node.val);nodeStack.push(node);levelStack.push(level);node = node.left;}TreeNode parent = nodeStack.pop();int parentLevel = levelStack.pop();node = parent.right;if (node != null && parent.left == null) {sb.append("()");rightCount++;}while (level > parentLevel) {sb.append(')');level--;}}while (level > -1) {sb.append(')');level--;}return sb.substring(1, sb.length() - 1);}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次,每个结点转换成字符串的时间都是 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是栈空间和转换成的字符串空间,栈空间取决于二叉树的高度,最坏情况下是 O ( n ) O(n) O(n),字符串空间取决于结点数,是 O ( n ) O(n) O(n)。






)

的)










)