
上一周的课程中讲了神经网络的结构以及正向传播(feed forward)过程,了解了神经网络是如何进行预测的,但是预测的结果怎么和真是结果进行比较以及发现了错误如何修改还没有提及。
这一周的课程中,介绍了cost function作为结果比较的标准以及backpropagation方法作为错误修改的方式。
Linear regression使用平方差来表示结果之间的差距:

Logistic regression使用negative log来表示结果之间的差距:

Neural network实际上就是k个Logistic regression的一个集合,所以其cost function也是negative log的一个集合。整个网络产生的error其实就是每一个Logistic regression产生的error的和。

在Logistic regression中,模型是向着error的负梯度方向更新的,所以需要计算cost function的梯度,这在Neural Networks中也是如此,只不过这次的权值θ多了一些,需要一层一层慢慢求解了。
假设神经网络有4层:
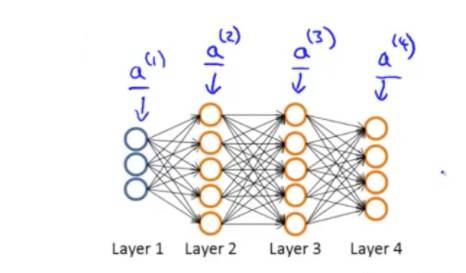
先来回顾一下,一条训练数据的正向传播的情况,这次我们不把bias直接加到矩阵中去了,把它拿出来,令为b(i),是一个列向量:
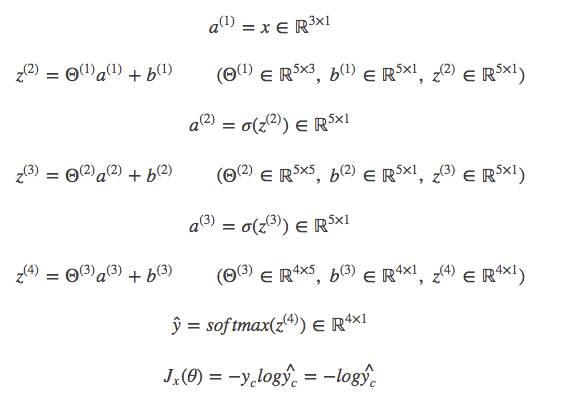






至此,所有的偏导都求完了,总结一下: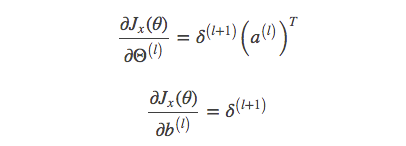
如果梯度计算不正确,那整个模型都错了。最惨的是,在训练了几个小时之后发现梯度算错了。所以梯度计算完之后,需要验算一下对不对。
梯度可以如下约等于:
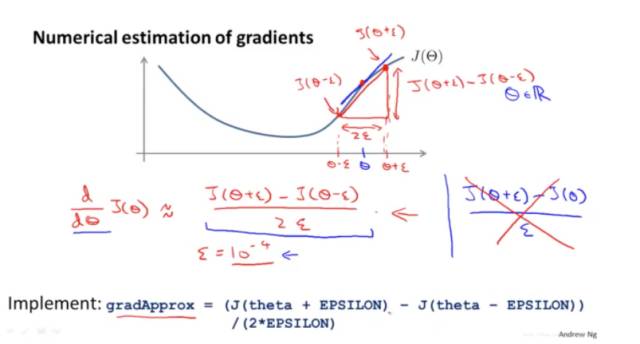
验算过程如下:

模型中权重和偏置的初始值可以随便设成任何数字,但是设置成什么样直接决定了模型收敛的快慢和程度,进而影响模型的performance。
把权重和偏置初始化为0非常不好。因为在前向传播过程中,全部初始化成0,则结果就是0,在得到残差之后,反向传播过程中,残差根据权重进行分配,因为权重全部为0,所以隐藏层的残差为0,即权重不更新,所以不能全部初始化成0,权重为0的神经元是死掉的,是不会更新的。
另外全部初始化成同样的数字也是不好的,模型将一直以同样的方式更新这些神经元。反向传播过程中,残差根据权重进行分配,因为权重都相同,所以权重的更新也是相同的,所以网络中的每一个神经元都是一样的。
一般从均匀分布中随机初始化权重和偏置,比如:













)




)

