全世界有3.14 % 的人已经关注了

数据与算法之美

消失的正方形

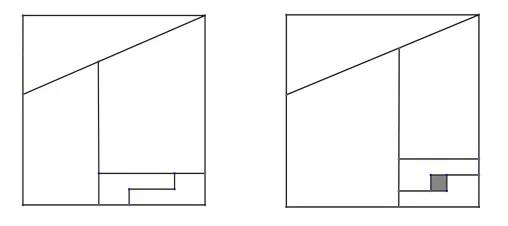
这是数学游戏大师马丁·加德纳在《从惊讶到思考》一书中提到过的例子。重新摆放分割的小块图形后，上面的正方形中少了一个小方格，它去了哪里？我们不妨实际操作一下，做两个全等的、上面没有孔洞的正方形（做的越大越好）。

把其中一个按图中的式样精确地剪成所需要的五块，然后重新安排一下，拼成右边的样子的。最后把它放到未经剪切的正方形上边，让二者的上边和两侧边都重合。你会发现，其实带方格的图形不是真正的正方形。它实际上是长方形，比正方形高 1／12。它的底部多出一个 12 * （1／12） 的窄带，其面积恰好等同于消失方格的面积。

所有三角形都是等腰三角形

这是一个颇为古老的数学把戏。最近又开始在网上流传。不妨来看看这个神奇的结论是如何得到的。

在一个任意△ABC中，做A点的角平分线，交BC边的垂直平分线A'O于点O。然后过O点分别做AB与AC边上的垂线，垂足为C'和B'。

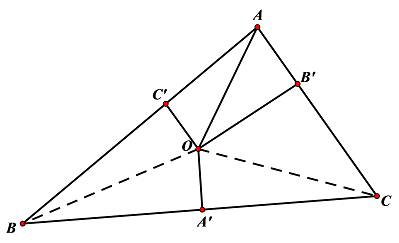
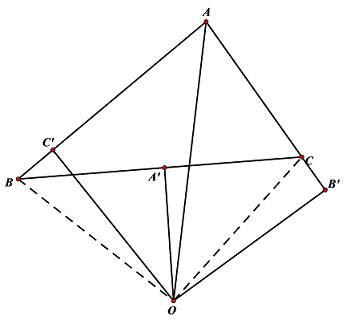
显然△AC'O≌△AB'O，所以 AC' = AB'， C'O = B'O又因为 BO = CO， ∠OB'C = ∠OC'B所以△BOC'≌△COB'。  推得： C'B = B'CAB = AC'+ C'B = AB' + B'C = AC，即△ABC是等腰三角形。

正如前面所说，平面几何的谬误大多都是在有误差的图上做文章的。实际上，角平分线会与其相对的垂直平分线并不相交于三角形内，而是交于三角形外部。所以即使有AC'=AB'，BC'=B'C，我们也能一眼看出AB=AC'+AB'，AC=BC'-B'C。

图里藏人

下面让我们见识一下什么是“大变活人”。

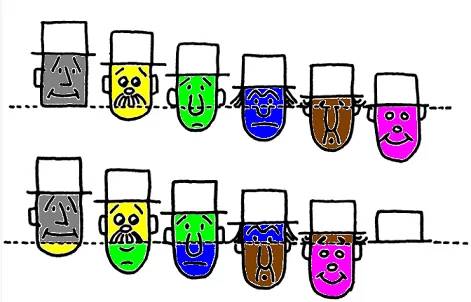
先看两排爷们的脸

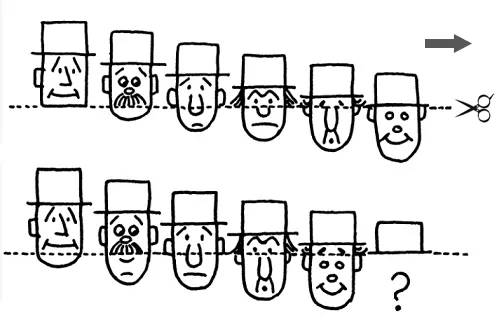
把上面的图从中间剪开，然后挪动成下图那样，怎么就少了一个人？

再看下面这张图。

上图仅仅通过两个动作，剪切和互换，就让人数在十二和十三之间变来变去，这是怎么回事？

眼尖的读者或许已经发现了，这种精心的安排其实是移花接木。以“爷们脸”这幅图为例（这幅图较简单），第一个人变成了圆下巴，第二个直接变成了双下巴，第三个的鼻子变大了，第四个的鼻子变长了，第五个换了一个表情，多了眉毛。

因为整个图的面积不变，但是脸个数少了一个，导致剩下的那些脸都变大了一些，其结果就是所有爷们个个是长脸。这种传递式的面积分配，很容易通过上色标记的办法清晰地辨认出来。

而至于第二个图，不得不说那是一个精妙无比的设计。不妨在图片变动之前，对十二个人编号。

再看看移动之后的号码变动情况，其中上身和下身都对应着各自的编号。

如果仔细看，便会发现移动之后1号小小地少了一撮头发，10号的鞋底也被削了一层。他们各自都被从身体的某个部位切割下一点东西，活生生拼凑出了一个人。当画面上出现13个人时，每个人都比出现12个时要矮 1／13。

两幅图的原理都是通过累积很多次细微尺寸的变化，最终改变图中物品的数量。第一幅较为简单，而第二幅用十二人切合成十三个，做了十二件事（从每个人身上“偷”一点），但却只用了两个动作！其精巧程度实在让人佩服。

有趣的是，有一种古老的伪造钱币的方法正是以这种原理为基础的。按照上面的方法可以类似地把九张钞票分成18份，重新安排成十张。但这样伪造的钞票很容易被侦破，不建议读者采用。因为票面上特殊的两个数字串，钱号在这种操作下已不相匹配。在所有的钞票上，这两个数字串都是位于相对的两端，一高一低。这正是为了挫败这种伪造企图。

看似一样的信息，不一样的结果

一位母亲有两个孩子，有人问母亲的朋友A，两个孩子都是女孩吗？这位朋友说：“我不清楚，但有一个是女孩”。母亲的另一位朋友B说：“我上次去她家，看到一个女孩”。朋友A听到，表示不屑：“这和我说的不是一样的吗”。

看起来这两个信息没有差别，但它们真的是等同的吗？

答案是：不同的。由A给出的信息可以推出两个孩子全是女孩的概率是1／3，而由B则是1／2。

让我们仔细分析一番。根据A的叙述，我们知道“两个小孩中有女孩”，而两个小孩的性别组合有四种情况：男男，男女，女男和女女。因为知道了两个小孩中有女孩，所以可以排除“男男”，两个小孩都是女孩的概率便是1／3。

而B的陈述是看到一个孩子是女孩，问题实际上就转化成了“另一个孩子是不是女孩”，因此两个小孩都是女孩的概率是1／2。

为什么呢？这是因为在进行概率计算的时候，不确定的描述往往意味着更多的可能性。一个类似的例子是，打牌的的时候，如果有人说，“来打个赌吧，我现在有一张A，猜猜我还有没有更多A？”这种情况下他很可能会输，但如果他报出抓到的那张A的花色，“我现在有一张黑桃A，猜猜我还有没有更多的A？”那结果就截然不同了。死理性派之前对此有过一个 详细的分析 。前一种情况下，有更多A的概率是 37% ,而后一种有更多A的概率一下就跃升为 56% 。面对这样反常的结果，不了解概率论的人，都会被吓一跳。

类似这样“想不通”的例子还有很多。比如著名的三门问题。换还是不换？这是一个让无数人纠结的问题，据说很多人在看了详尽的分析后，依然觉得有违常理，不能接受。

“最高IQ人类”的玛丽莲在当年公布自己的答案——换一扇门时，立刻引来巨大争议，无数人觉得她回答错了，并写信“纠正”她，这些记录都保留在它的个人网站上。就是直到今天，这个游戏依然困扰着不少人。

双赢的赌局

甲和乙各自收到女朋友送的领带。两人见面开始争论谁的更贵，最终决定打个赌，去商场调查，谁的领带贵谁就算赢， 而赢的人要把领带送给输的人作安慰 。

甲认为他在这个赌局中输赢是等概率的。如果赢了，那么失去的是自己戴的这条领带。而如果输了，则会得到一个更贵的领带。所以这个赌局对他是有利的。

当然乙也可以这样想。但问题是，打一次赌怎么会同时对双方都有利呢？

这个著名的问题由法国数学家莫里斯•克莱特契克在他的《数学消遣》书中首先提出。他指出，要想这个游戏公平，必须限制条件。比如甲乙二人对对方女朋友的阔绰程度一无所知等。如果说甲的女朋友出手相对更阔绰些，那么甲的领带就有较大的可能比乙的要贵，他就更倾向于输掉这次打赌。

这个例子后来衍化成著名的钱包悖论，道具由领带变为了钱包：由第三者计算甲、乙二君钱包里面的钱，钱少者可以赢走钱多者的钱。

实际上，甲、乙二人的错误在于，他们只根据“可以赢更多的钱”这点，就做出这场赌博对自己有利的结论。但这场赌博对谁有利，应该以谁可以“赢得这场赌博”而不是“可以赢更多的钱”来判断。以赌谁钱包里钱少为例。

判断谁有胜算，必须注意两点：

• 必须计算期望值。

• 钱包里有多少钱是很随机的。

所以正确的逻辑应为：

• 如果我的钱包里有较多的钱，那么我参加这个游戏，会输掉较多的钱。

• 如果我的钱包里有较少的钱，那么我参加这个游戏，会赢得较多的钱。

这两种情况的可能性是均等的。而且，由于总有一个人赢得另一个人输掉有更多钱的钱包，这个游戏是均衡的。

所以它的结果应该是甲、乙各有一半的可能获胜。也就是说，这个游戏是公平的 ，并不对哪一方有利。

作者：严酷的魔王

版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请留言联系删除，感谢合作。

精品课程推荐：

选购数学科普正版读物

严选“数学思维好物”

送给孩子的益智礼物   |   办公室神器

算法工程师成长阅读   |   居家高科技

理工科男女实用型礼物精选   

数据与算法之美

用数据解决不可能

长按扫码关注