全世界只有3.14 % 的人关注了
青少年数学之旅
泰勒展式 (Taylor expansion) 的剩余项救人一命！
在俄国革命期间（1917年左右），数学物理学家塔姆 (Igor Tamm) 外出找食物，在靠近敖德萨 (Odessa) 的乡间被反共产主义的保安人员逮捕。保安人员怀疑他是反乌克兰的共产主义者，于是把他带回总部。
- 头目问：你是做什么的？
- 塔姆：我是一位数学家。
头目心存怀疑，拿着枪，手指扣着扳机，对准他。
手榴弹也在他的面前晃动。
- 头目说：好吧，那么一个函数作泰勒展开到第 n 项之后，你就把误差项算出来。如果你算对了，就放你一条生路，否则就立刻枪毙。
于是塔姆手指发抖，战战兢兢地慢慢计算，当他完成时，头目看过答案，挥手叫他赶快离开。
塔姆在1958年获得诺贝尔物理奖，但是他从未再遇到或认出这位非凡的头目。
笔者讲授微积分，每教到泰勒定理时，都要顺便说这个故事，让学生警惕一番。
泰勒展开定理就是要利用微分与积分工具，来剖析函数的结构。
假设函数 f 定义在开区间 (a,b) 上，并且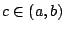 
，当我们知道 f 的资讯越多，对f 的剖析就越精细。
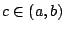，当我们知道 f 的资讯越多，对f 的剖析就越精细。这个资讯包括两方面，一个是 f 的可微分的阶数逐渐提高，这是一种泛泛的条件；另一个是 f 在一点 c 的各阶微分系数的阶数也不断增加，这是在一点（局部）的资讯之逐渐加深。
- (i) 若 f 为一阶连续可微分，并已知 f(c) 之值，那么由微积分根本定理的 Newton-Leibniz 公式知
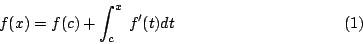亦即 f(x) 可以剖析为清楚的 f(c) 与尚未完全清楚的
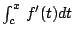两项之和。 - (ii) 若 f 为二阶连续可微分，并且已知 f(c) 与 f'(c) 的值，那么由(1)式与分部积分公式得知
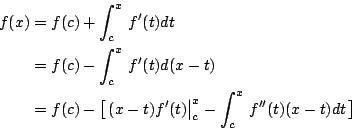从而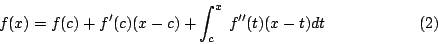
亦即 f(x) 可以剖析为清楚的一次多项式 f(c)+f'(c)(x-c) 与尚未完全清楚的
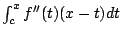。 - (iii) 若 f 为三阶连续可微分，并且已知f(c), f'(c) 与 f''(c) 之值，那么由(2)式与分部积分公式得知
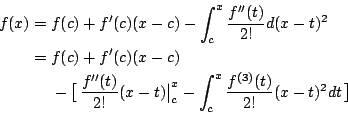从而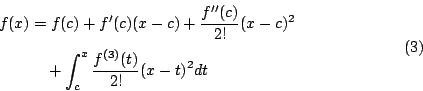
亦即 f(x) 可以剖析成清楚的二次多项式
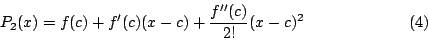与尚未完全清楚的剩余项
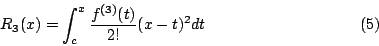利用积分的平均值定理，(5)式又可以写成
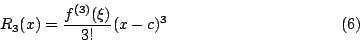我们称 P2(x) 为二阶泰勒多项式。
按上述要领，继续做下去（数学归纳法），我们就得到如下美丽的泰勒展开定理。
- 泰勒展开定理（1715年）：
- 设函数 f 在区间 (a,b) 上具有 n+1 阶连续地可微分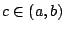，，则对任意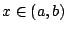
，f(x) 可以展开成 
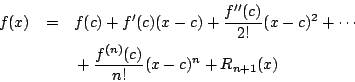其中的剩余项（或误差项）Rn+1(x) 可以表成微分形式或积分形式：
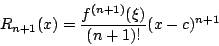其中 ξ 介于 c 与 x 之间，或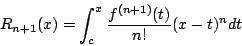
注：泰勒（B. Taylor, 1685～1731）是牛顿的学生，具有相当的音乐与艺术才华。他为了探求音律之谜，首开其端用微积分来研究弦振动问题（1713年），约一个世纪之后，富立叶（Fourier）分析出现才达于高潮（1807年）。泰勒也研究投影画法的几何学，其美术作品至今仍然被珍藏于伦敦的国家画廊（the National Gallery）之中。
参考来源：http://9yls.net/4413.html版权归原作者所有，转载仅供学习使用，不用于任何商业用途如有侵权请留言联系删除，感谢合作。
写在最后
微信公众号“少年数学家”
提供丰富的数学课外知识
数学人物、数学趣谈、科技与数学
想让孩子懂得更多有趣的数学
记得关注“少年数学家”
)