本节主要说了递归的设计和算法实现,以及递归的基本例程斐波拉契数列、strlen的递归解法、汉诺塔和全排列递归算法。
一、递归的设计和实现
1.递归从实质上是一种数学的解决问题的思维,是一种分而治之的思想。
这个是常见的一种数学算法,其实它就是递归的本质。我们要求的是所有数的乘积,那么我们就先求出两个数的乘积,然后再根据这两个数的乘积去求第三个数的乘积,这样每一次我们实际上都是进行的两个数的相乘,也就是我们把一个很多个数的相乘转换为了两个数的相乘。
2.通过上面的例子可以发现,递归就是将大型复杂问题转化为与原问题相同,但是规模变小的问题进行处理。
4.同时我们可以发现a1 这个时候n==1,是一个特殊的条件。这就是递归的边界条件,最后的最后我们都会执行到递归的边界条件,然后再从边界条件返回。等到都返回结束后我们就真正实现了我们想要的结果。
5.如果递归没有边界条件,那么我们的递归将永远无法跳出,也就是这个问题递归是无法解决的。
6.在解决递归问题的时候首先要建立递归模型,这是解决递归类问题的第一步。但是说来容易,其实这是一个痛苦的过程,说白了,算法不是一般人能搞的。
二、斐波拉切数列的递归实现
1.斐波拉切数列实际上就是一个递归的典型表现,它的具体要求如下:
通过上图我们可以知道,斐波拉契数列的要求就是求相邻两个的数和然后赋给第三个数。这样我们可以先求前两个数的和,然后再求第二个与第三个数的和,一直求到最后,然后再返回。
2.假定我们要求的数列的元素个数为10
那么具体程序如下所示:
#include <stdio.h>int fibonacci(int n)
{if( n > 1 ){return fibonacci(n-1) + fibonacci(n-2);}else if( n == 1 ){return 1;}else if( n == 0 ){return 0;}
}int main()
{int i = 0;for(i=1; i<=10; i++){printf("fibonacci(%d) = %d\n", i, fibonacci(i));}return 0;
}通过上面的程序可以看出:我们首先通过主函数调用fibonacci函数,然后通过for循环依次向里面传递值,第一次传递的值为1,返回的值为1,所以打印1.第二次传递的值为2,符合if(n>1)的条件,执行语句
fibonacci(n-1) + fibonacci(n-2);这个时候产生第一轮递归,也就是先执行函数fibonacci(1)执行以后的返回结果是1,再执行fibonacci(0),执行以后的返回结果是0,所以这一轮的返回结果是是1.
继续调用fibonacci函数,传递的参数是3,然后依次向后执行,每一次的递归深度都在加深。
三、strlen函数使用递归方式实现
1.我们都知道strlen函数的使用方法,它是通过传递进来的字符串来判断字符串的大小,但遇见"\0"的时候返回字符的个数,"\0"不包括在内。
2.假定我们要求一个"12345"的字符串的长度,具体例程如下:
#include <stdio.h>int strlen(const char* s)
{if( s == NULL ){return -1;}else if( *s == '\0' ){return 0;}else{return strlen(s+1) + 1;}
}int main()
{printf("strlen(\"12345\") = %d\n", strlen("12345"));printf("strlen(NULL) = %d\n", strlen(NULL));printf("strlen(\"\") = %d\n", strlen(""));return 0;
}程序分析:我们在主函数中调用strlen函数,在我们第一次进入strlen函数的时候,程序执行判定,都不满足前两个判定,程序继续向下执行,再次调用strlen函数,然后再进行判定,仍然不满足判定条件,一直执行到s指针指向'\0',这个时候各个调用函数开始返回,最外层的返回0,0+1,第二层返回1,1+1,第三层返回1,1+1 。直至所有函数全部返回。程序打印结果如下所示:
整个程序我们是把一个字符串的长度求解过程转变成了对每一个字符长度的求解,然后再进行相加,边界条件就是'\0'。
四、汉诺塔递归算法的实现
1.汉诺塔的要求我就不详细说了,汉诺塔的问题我想了足足一天,其实最后也是单步调试加上草稿纸才把它搞定,这里拿三个盘子作为分析。
2.汉诺塔的递归思想:第一,把a上的n-1个盘通过c移动到b。第二,把a上的最下面的盘移到c。第三,因为n-1个盘全在b上了,所以把b当做a重复以上步骤就好了。
3.汉诺塔的具体代码实现:
#include <stdio.h>void hanoi(int n, char a, char b, char c)
{if( n > 0 ){if( n == 1 ){printf("%c -> %c\n", a, c);}else{hanoi(n-1, a, c, b);printf("%c -> %c\n", a, c);hanoi(n-1, b, a, c);}}
}int main()
{hanoi(3, 'a', 'b', 'c');getchar(); return 0;
}
程序打印结果如下:
五、汉诺塔递归调用分析
因为为了调试方便观看值,所以我把a,b,c字符重新定义成了整型变量,具体程序如下:
#include <stdio.h>void hanoi(int n, int a, int b, int c)
{if( n > 0 ) {if( n == 1 ){printf("%d -> %d\n", a, c);}else{hanoi(n-1, a, c, b);printf("%d -> %d\n", a, c);hanoi(n-1, b, a, c);}}
}int main()
{hanoi(3, 5, 6, 7);return 0;
}1.从主函数中调用hannoi函数,传递的参数是:n=3,a(1)=5,b(1)=6,c(1)=7
2.第1次进入hannoi函数,执行if(n==1)判定,不符合条件,调用hanoi(n-1,a,c,b)函数
3.向hannoi传递的参数是:n=2,a(2)=a(1),b(2)=c(1),c(2)=b(1)
4.第2次进入hannoi函数,执行if(n==1),不符合条件,调用hanoi(n-1,a,c,b)函数
5.向hannoi传递的参数:n=1,a(3)=a(2),b(3)=c(2),c(3)=b(2)
6.第3次进入hannoi函数,执行if(n==1)判定,符合条件,执行打印函数printf("%d->%d\n",a,c)这个时候打印函数里面的a,c是第3次调用hannoi函数传递进来的参数,也就是a3),c(3),追到原始值也就是a(1),c(1)。打印结果是:5->7
7.n=3的hannoi函数调用结束,子函数第1次执行结束。返回到n=2的hannoi函数调用位置,程序继续向下执行
8.调用打印函数:printf("%d->%d\n",a,c),这个时候打印函数的参数是n=2的时候hannoi函数的参数,也就是
a(2),c(2),追到原始值a(1),b(1)。打印结果是:5->6
9.执行完打印函数以后程序继续向下执行,调用hanoi(n-1,b,a,c)函数
10.这次调用hanoi(n-1,b,a,c)是从n=2的hannoi函数开始的,所以向hannoi函数传递的参数是:n=1,a(4)=b(2),b(4)=a(2),c(4)=c(2)
11.第4次进入hannoi函数,指定if(n==1)判定,符合条件,执行打印函数printf("%d->%d\n",a,c)这个时候打印函数里的a,c是a(4),c(4),追到原始值c(1),b(1),打印结果是:7->6.
12.调用hanoi(n-1,b,a,c)函数结束,程序返回到调用hanoi(n-1,b,a,c)函数的位置,接下来程序没有语句,子函数再次结束,程序返回到n=3调用hannoi函数的位置,执行印函printf("%d->%d\n",a,c),这个时候打印函数里的参数a,c是n=3的时候的参数,也就是a(1),c(1),追到原始值。打印结果是:5->7。
13.程序继续向下执行,调用hanoi(n-1,b,a,c)函数
14.这个时候第一轮递归已经结束,向hannoi传递的参数是:n=2,a(5)=b(1),b(5)=a(1),c(5)=c(1)
15.第5次进入hannoi函数,执行if(n==1)判定,不符合条件,调用hannoi(n-1,a,c,b)函数
16.向hannoi传递的参数是:n=1,a(6)=a(5),b(6)=c(5),c(6)=b(5)
17.第6次进入hannoi函数,执行if(n==1)判定,符合条件,执行打印函数printf("%d->%d\n",a,c)这个打印函数里面的参数a,c是第6次调用hannoi函数的参数,也就是a(6),c(6),即b(1),a(1),追到原始值为6,5,打印结果是6->5
18.这个时候第6次进入hannoi函数执行完毕,程序返回到第六次调用hannoi函数的位置,继续向下执行。
19.调用打印函数printf("%d->%d\n",a,c),这个时候打印函数的参数a,c是n=2的时候第5次调用hannoi函数传递的参数,也就是a(5),c(5),追到原始值是b(1),c(1),即6,7.打印结果是6->7
20.程序继续向下执行,调用hanoi(n-1,b,a,c)函数,这个时候程序是从n=2的hannoi函数位置继续向下执行的,参数是:n=1,a(7)=b(5),b(7)=a(5),c(7)=c(5)
21.第七次进入hannoi函数,进行if(n==1)判定,符合条件,执行打印函数printf("%d->%d\n",a,c),这个时候打印函数的参数是第七次调用hannoi函数的参数,也就是a(7),c(7)即b(5),c(5),追到原始值5,7打印结果是:5->7
22.程序最后再一次返回两次调用hanoi(n-1,b,a,c)函数的位置,但是每一次返回都没有其他动作,直至程序结束。
程序分析的结果十分复杂和繁琐,而且这仅仅是三层盘子。同时由于自己的画图水平不好,所以也没有画流程图,同时网上好多大牛说是可以用树的想法去想汉诺塔问题,但是我没学习到树,所以只能用上面那种最笨额方法了。
六、全排列的递归调用
1.问题的提出:假定有三个元素a,b,c,那么这三个元素的全排列有六种方式:abc,acb,bac,bca,cba,cab。那么两个元素的全排列的是ab,ba,一个元素的全排列就是元素本身,所以一个元素的全排列就是递归的边界条件。
2.我们这里以三个元素的全排列,程序例程如下:
#include <stdio.h>void permutation(char s[], int b, int e)
{if( (0 <= b) && (b <= e) ){if( b == e ){printf("%s\n", s);}else{int i = 0;for(i=b; i<=e; i++){char c = s[b];s[b] = s[i];s[i] = c;permutation(s, b+1, e);c = s[b];s[b] = s[i];s[i] = c;}}}
}int main()
{char s[] = "abcd";permutation(s, 0, 3);return 0;
}
程序的递归算法框图如下所示:
由于我们传进子函数的四个字符的字符数组,所以这里我们直接执行else部分的函数,首先执行for循环,for循环从i=b开始,这样我们第一轮for循环先做的交换代码如下:
char c = s[b];
s[b] = s[i];
s[i] = c;其实这个时候我们没有完成任何交换,然后继续调用permutation(s, b+1, e)函数,再次进入for循环,这个时候for循环是从i=b+1开始的,这个时候执行交换部分的代码还会完成另一个元素的交换。实质上这个交换部分的代码完成的就是将每一个元素作为第一个位置的作用,然后再进行其他操作。
for循环里的第二部分主要代码如下:
c = s[b];
s[b] = s[i];
s[i] = c;这一部分代码的主要作用是在每一个permutation(s, b+1, e)进行弹出操作的时候开始执行,这样我们就可以对后面的数进行全排列了。我们也就完成图示的全排列操作。具体的递归过程可以例程单步调试来进行理解。
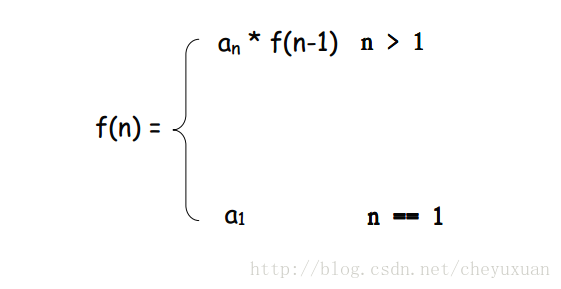
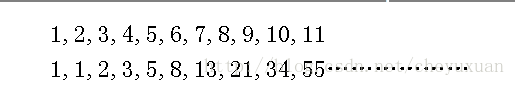


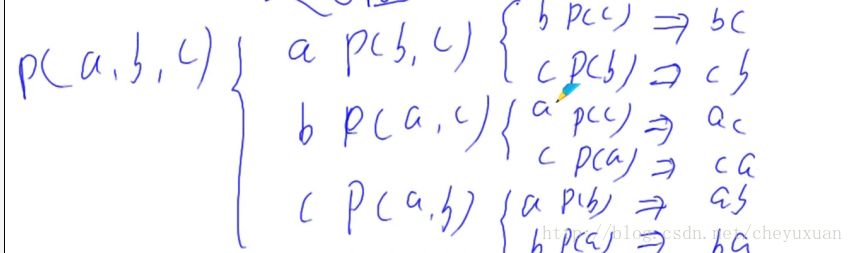







:one-to-one关系映射)








)


