例1：

已知一次函数y＝3x＋m的图像与一次函数y＝4－2x的图像交点在x轴上，求m的值．

分析：

本题中，y＝4－2x的函数表达式确定，则其与x轴的交点坐标确定，因此，只需求出该点坐标，代入至y＝3x＋m中，即可求出m的值．

解答：

∵令y＝4－2x＝0，x＝2，

∴交点(2，0)，

把(2，0)代入y＝3x＋m得，

3×2＋m＝0，m＝－6．

例2：

分析：

显然，两直线与y轴的交点分别是(0，－3)，(0，2)，因此只可能交在x轴上，分别算出两直线与x轴交点坐标，得到a与b的比值．

解答：

例3：

若以二元一次方程2x－y＋b＝0的解为坐标的点(x，y)都在函数y＝2x－b＋1的图像上，则常数b＝_______．

分析：

由题意可知，把二元一次方程2x－y＋b＝0经过变形，写成一次函数的形式，一定与函数y＝2x－b＋1是一致的，从而可以求b．

解答：

2x－y＋b＝0，y＝2x＋b，

∴2x＋b＝2x－b＋1

－b＋1＝b，解得b＝0.5．

例4：

已知一次函数y＝2x＋1的图像和一次函数y＝3x＋b的图像的交点在第三象限，求b的取值范围．

分析：

本题中，需要将两个一次函数联立方程组，用含b的代数式表示交点坐标，再根据第三象限点的坐标特征得到关于b的不等式组，确定b的范围．

解答：

例5：

无论m取何值，一次函数y＝x＋2m的图像与y＝－x＋4的图像交点都不可能在第几象限?

分析：

本题若与例4一样，先将两个一次函数联立方程组，用含m的代数式表示交点坐标，要分情况讨论m的范围，非常繁琐．仔细观察，便可知直线y＝－x＋4的图像是确定的，不经过第三象限，所以无论m取何值，两函数图像的交点都不会经过第三象限．

解答：

第三象限．

例6：

分析：

本题中，不得不先解方程，用含a的代数式表示x、y的值，然后对x、y进行正负性分析，从而确定不经过第几象限．

解答：

例1：

如图，若一次函数y＝－2x＋b的图像交y轴于点A(0，3)，则不等式－2x＋b＞0的解集为________．

分析：

首先，根据点A坐标，确定直线解析式，不等式－2x＋b＞0，表示y的值为正，则对应的函数图像是直线落在x轴上方的部分，而要求对应的x的取值范围，则需求出函数图像与x轴交点的横坐标，从而得出在临界点的左侧还是右侧．

解答：

例2：

函数y＝ax＋b图像经过一、二、三象限，且与x轴交于点(－2，0)，求ax＞b的解集______．

分析：

我们可以先大致画出y＝ax＋b的图像，要求ax＞b的解集，也就是求ax－b＞0的解集，则转化成求函数y＝ax－b对应的图像中，直线落在x轴上方的部分的x的范围，画出y＝ax－b的图像，与y＝ax＋b平行，与y轴交点(0，－b)，从而可知与x轴交点(2，0)．

解答：

例3：

分析：

首先利用待定系数法求出A点坐标，－2x＞ax＋3，

表示y1＞y2，即函数y1的图像要在函数y2的图像的上方，从而确定x的解集．

解答：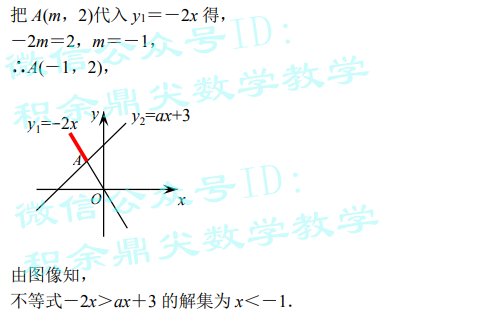

例4：

分析：

要求这个不等式组的解，我们可以拆成两部分，

第一部分，kx＋b＞0，即求y＝kx＋b的图像在x轴的上方时，对应x的范围．

第二部分，kx＋b＜mx，即求y＝kx＋b的图像在y＝mx的图像的下方时，对应x的范围．

解答：

例5：

分析：

解答：

例1：

分析：

首先把两个函数联立方程组求得交点坐标，再分别求得两个函数与x轴的交点坐标，据此画出图像，可以求得三角形的面积．

解答：

例2：

分析：

要求BC，首先求OA，则联立两一次函数的解析式，求出x、y的值，即可得出A点坐标．利用勾股定理可得OA的长，故可得出BC的长．由P(a，0)可知，点B，点C的横坐标与点P横坐标相同，用含a的代数式表示出B、C的纵坐标，纵坐标相减的绝对值，即为BC长．

解答：