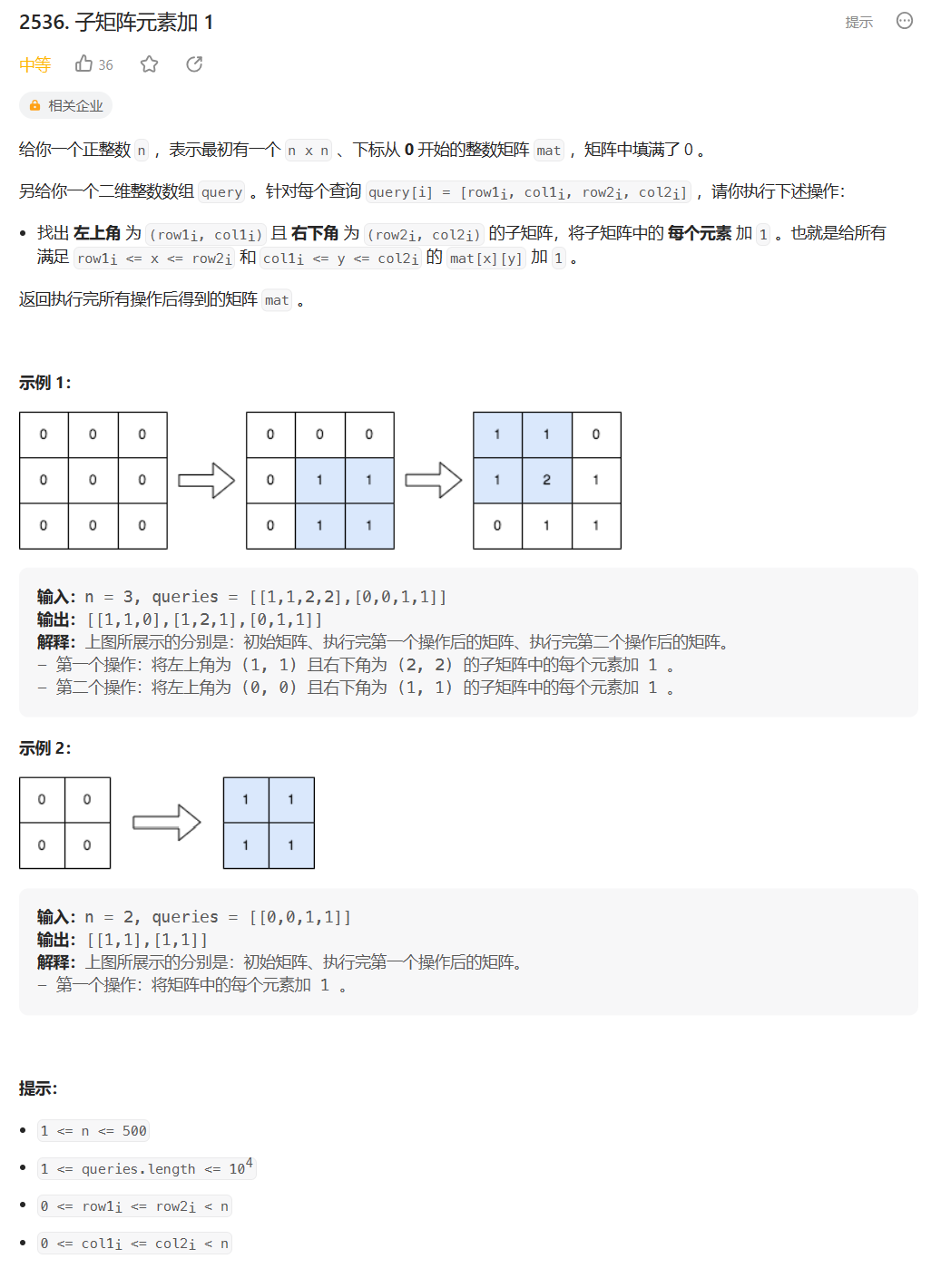
暴力解法：直接按照题目所示在矩阵的相应位置加一

时间复杂度：O(n2 * queries.length)

空间复杂度：O(1)

二维差分：创建二维差分数组，通过对差分数组的修改来影响原来的数组，最后还原

时间复杂度：O(n2 + queries.length)

空间复杂度：O(n2)

示例2此种情况会发生角标越界的情况，因此差分数组需要多初始化2行2列

代码

import org.junit.Test;public class SubmatrixPlus {@Testpublic void test() {int[][] queries = new int[][]{{1, 1, 2, 2}, {0, 0, 1, 1}};for (int[] query : submatrixPlus(queries, 3)) {for (int n : query) {System.out.print(n + " ");}System.out.println();}int[][] queries1 = new int[][]{{0, 0, 1, 1}};for (int[] query : submatrixPlus(queries1, 2)) {for (int n : query) {System.out.print(n + " ");}System.out.println();}}//int[][] querries = {{左上角行，左上角列，右下角行，右下角列}，{左上角行，左上角列，右下角行，右下角列}}public static int[][] submatrixPlus(int[][] queries, int n) {// 构建差分数组,多初始化2行2列避免数组越界int[][] arr = new int[n][n];for (int i = 0; i < queries.length; i++) {arr[queries[i][0] + 1][queries[i][1] + 1]++;//第几行不等于数组的索引arr[queries[i][2] + 2][queries[i][1] + 1]--;arr[queries[i][0] + 1][queries[i][3] + 2]--;arr[queries[i][2] + 2][queries[i][3] + 2]++;}//还原数组int[][] res = new int[n + 2][n + 2];for (int i = 0; i < res.length; i++) {for (int j = 0; j < res[i].length; j++) {arr[i + 1][j + 1] = arr[i + 1][j + 1] + arr[i + 1][j] + arr[i][j + 1] - arr[i][j];res[i][j] = arr[i + 1][j + 1];}}return res;}
}