之前在不经意间也有接触过求突变点的问题。在我看来,与其说是求突变点,不如说是我们常常玩的"找不同"。给你两幅图像,让你找出两个图像中不同的地方,我认为这其实也是找突变点在生活中的应用之一吧。回到找突变点位置上,以前自己有过一个傻傻的方法:就是直接求前后两个采样的的差分值,最后设置一个阈值,如果差分值大于这个阈值则该点是突变点。但这个方法问题很大,实际中突变点幅值有大有小,你怎么能确定阈值到底是多少呢?还有可能信号本来的差分值就比你那突变点的差分值还要大。所以这种方法在信号或噪声稍微复杂一点就行不通了。
这几天看到了一种船新的信号突变点检测的方法-基于小波变换的信号突变点检测。于是乎去学习了一下小波变换的相关知识和应用,学习的不是很深入,但也模模糊糊感觉到了小波变换确实是检测突变点的一大利器,下面分为两个大部分总结一下我所学习到的小波变换求突变点的实现过程和相关知识理论。
一:小波变换求信号突变点实现
我喜欢直接从应用入手,或者应用结合理论。一步一步分析代码,看数据和图像的变化比一步一步推公式有趣的多(虽然可能是错误的呀)。于是在这里我就先直接上代码和图像了,这样先让我们对整个过程有个感性的认识。
1.1 原始信号的生成
首先生成原始信号,这里随便什么信号都可以,那我就生成一个正弦信号吧,具体信号参数见代码注释。
clear all; close all; clc;
Fs = 1000; % 采样频率1000Hz
Ts = 1 / Fs; % 采样时间间隔1ms
L = 1000; % 采样点数1000
t = (0 : L - 1) * Ts; % 采样时间。1000个点,每个点1ms,相当于采集了1s
x = sin(2 * pi * 10 * t); % 原始正弦信号,频率为10Hz,振幅为1

1.2 添加突变点
第二步我们要人为添加突变点了,为了看起来直观就暂时不添加噪声了。此处我们添加两个突变点,将第233个点的幅度在原本基础上增加0.5,将第666个点的幅度在原本基础上增加0.1,代码和添加后信号图像如下:
x(233) = x(233) + 0.5;
x(666) = x(666) + 0.1;
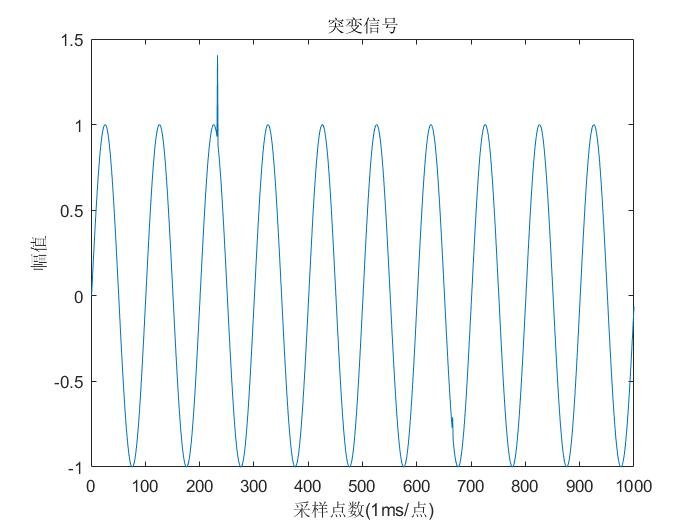
可以看到一个突变点很明显,而另一个却不是那么的明显,可能肉眼看的话都会忽略掉这个突变点。
1.3 对信号做傅里叶变换
可能有人要问,既然我们做的是小波变换,为什么又要对信号做傅里叶变换呢?其实我们确实可以不用做傅里叶变换的,但是为了与小波变换做对比,分析各自的优势和劣势,我们还是看一下该突变信号的傅里叶变换。
Y = fft(x,1024);
f = Fs * (0 : (L / 2)) / L;
P2 = abs(Y / L);
P1 = P2(1 : L / 2 + 1);
plot(f,P1)

1.3.1 补充
下面我们再给一个原始信号的fft幅度谱。从肉眼来看,我们可以发现原始信号和添加突变信号的频域差别不大,只是突变信号的频谱在高频部分多了些抖动。所以要从傅里叶变换的频域来检测突变信号是不合适的。具体原因在第二部分会有总结,主要是两个变换选取“基”的不同而导致的。
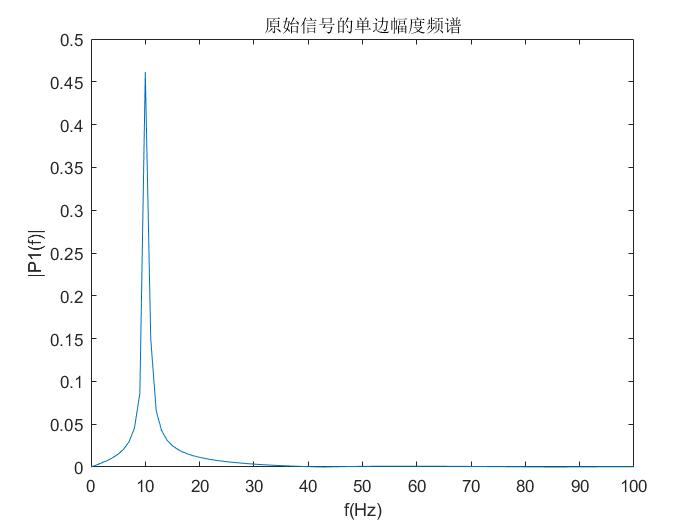
1.4 对信号做小波变换
重头戏小波变换来了,这里我们用两种小波变换的方法检测突变点,一是连续小波变换;二是离散小波变换,这里只会简略说明一下图像,可以结合第二部分原理一起查看。
1.4.1 连续小波变换
我们对突变信号进行连续小波变换,实现代码和图像如下:
cw1 = cwt(x,1:32,'sym2','plot'); % 对信号做连续小波变换
title('连续小波变换');
cwt(Continuous wavelet transform)函数表示进行连续小波变换,主要是处理一维的数据,比如我们这个数据。参数x是输入的信号;1:32表示尺度参数Scales的取值范围为(1:32);'sym2’表示我们用的小波是sym2小波;'plot’是画出连续小波变换系数的意思。运行图像如下:
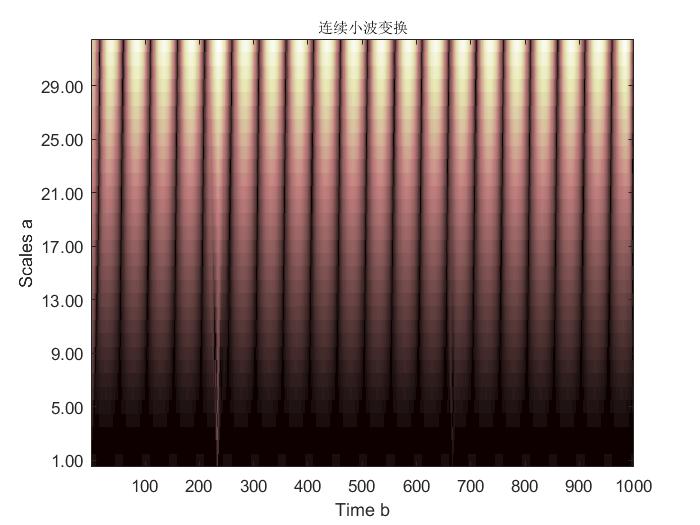
不同于傅里叶变换只有w一个自变量,小波变换有两个自变量,分别是a(尺度参数)和b(位移参数)。从上图我们可以看出在小波位移到第233个点和第666个点,且a较小时,可以看到一条较亮的白条,可以暂且理解成小波在这个位移和尺度上与信号相关性较大。在某个位置出现小波与信号相关性激增的原因就是信号在这个位置出现了突变,于是我们就愉快的找到了两个突变点的位置。
1.4.2 离散小波变换
由于连续小波变换的位移参数(b)和尺度参数(a)都是连续变化的,特别是尺度参数的连续变化,会带来巨大的计算量,于是利用离散小波变换来处理信号,一种方法是我们可以直接取离散的a和b的值,然后计算得到其系数图,从不同的尺度观察信号的特征,例外一种更常用的离散小波变换方法叫做Wallat算法,是通过构造一个低通滤波器和一个高通滤波器不断对信号进行滤波,从而得到信号不同频率的细节的方法。这里还是主要说代码和图像,具体实现原理在第二部分有粗浅介绍。
wavedec(x,3,‘db4’)函数表示进行离散小波多层分解,x是待处理的输入信号;3表示进行3层分解,'db4’是一个小波的名字。处理完毕后得到1、2、3层的细节系数(details)d1、d2、d3和第3层的近似系数(Approximations)a3。本段代码和分解后的图像如下:
[d,a]=wavedec(x,3,'db4'); %对原始信号进行3层离散小波分解
a3=wrcoef('a',d,a,'db4',3); %重构第3层近似系数
d3=wrcoef('d',d,a,'db4',3); %重构第3层细节系数
d2=wrcoef('d',d,a,'db4',2); %重构第2层细节系数
d1=wrcoef('d',d,a,'db4',1); %重构第1层细节系数
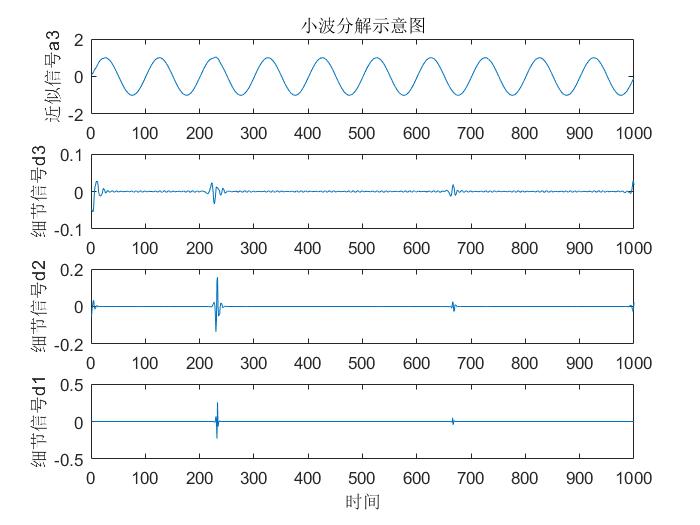
我们还可以用另一个函数dwt()来手动进行一层一层的分解,不过注意分解过后每一层的分解信号长度会少一半,因为进行了下采样。具体原因可见第二部分的介绍,手动分解的代码和分解图像入下:
[ca11,cd1] = dwt(x,'db4'); % 第1层分解
[ca22,cd2] = dwt(ca11,'db4'); % 第2层分解
[ca3,cd3] = dwt(ca22,'db4'); % 第3层分解
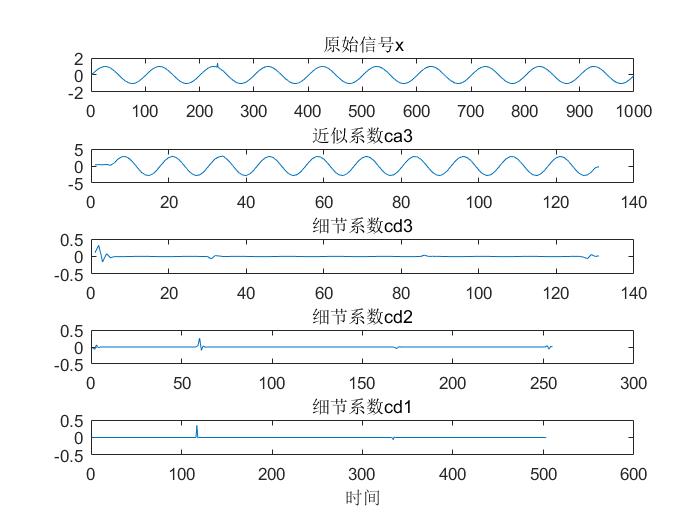
由上图可明显看出,除去开头和结尾的一些比较大的点外,在第1、2、3层的细节信号中,最大值点恰恰是第233点和第666点,于是也可以愉快的可以确定这两个点即是突变信号的位置了。
这里还可以稍微注意一下近似信号a3,它类似于原始信号滤去了高频成分的样子,它是怎么得来的你看了第二部分就知道了!
1.5 总结
在这一部分中我们直抓要害,知道了怎么通过小波变换来检测信号的突变点,MATLAB的函数用起来就是爽有木有。但是能应用是一回事,我们还是尽量多了解一下小波变换的原理为好。小波是怎么构造的,它的性质有什么?连续小波变换的图像是怎么计算出来的呢?离散小波变换的每一层又是怎么算出来的呢?只有学习了它们背后的支撑运算的数学公式,我们才能算真正理解了它。
二:小波变换的基础知识
关于基础知识这一部分,主要都是参考的[2]里面的内容,我只是提炼了一些我认为重要的内容写出来,然后有自己小小的补充。
2.1 连续小波变换(CWT)
首先直接给出连续小波变换公式:
C ( a , b ) = 1 a ∫ R f ( t ) ψ ∗ ( t − b a ) d t C(a,b) = \frac{1}{\sqrt{a}} \int_R f(t) \psi^*(\frac{t-b}{a})dt C(a,b)=a1∫Rf(t)ψ∗(at−b)dt
连续小波变换的结果就是得到很多个小波系数 C ( a , b ) C(a,b) C(a,b),它有两个自变量参数,分别是尺度参数a和位移参数b。注意在CWT中a和b都是连续变化的。
2.1.1 尺度参数与位移参数
尺度变换:
如何对小波进行尺度变换呢?其实就是简单的拉伸或者压缩,下图表现为一个小波在不同的尺度参数下的变换,可以看到尺度参数a越小,小波越压缩,频率越高;尺度参数a越大,小波越拉伸,频率越低。
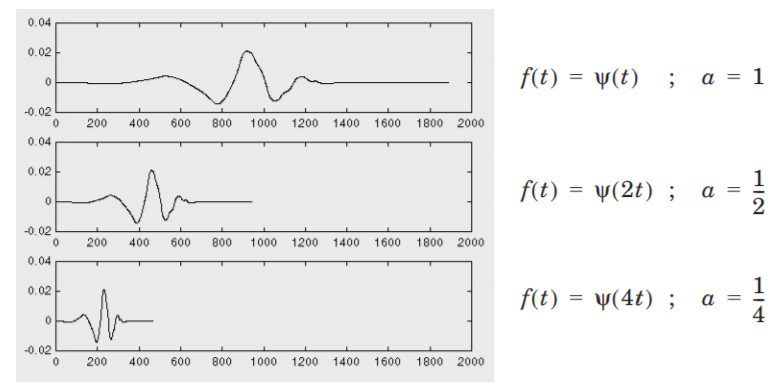
位移变换:
位移变换意味着将小波延迟或提前,如下图将小波 ψ ( t ) \psi(t) ψ(t)往右移位长度k得到 ψ ( t − k ) \psi(t-k) ψ(t−k)。
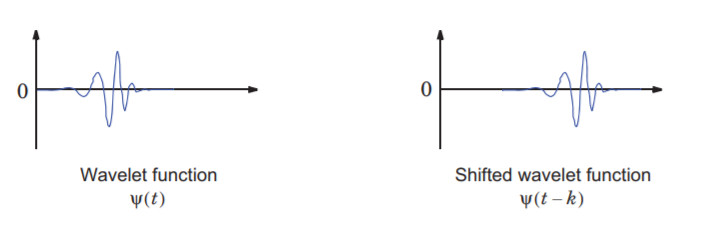
2.1.2 连续小波变换具体过程
连续小波变换其实就是把小波从小尺度拉伸到大尺度,然后把不同尺度的小波依次从0位移到信号的完整长度,并不断地计算它们的积分的过程。详细来说就是下面几个步骤:
- 将小波 ψ ( t ) \psi(t) ψ(t)放到原始信号 f ( t ) f(t) f(t)的开头处进行比较。
- 计算小波系数C,C其实也表示了小波与信号这一部分的相关程度。C越大,说明相似度越高。
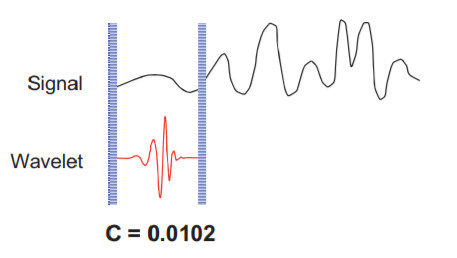
- 将小波向右平移,距离为b,小波函数变为 ψ ( t − b ) \psi(t-b) ψ(t−b)。并且重复步骤1和2,直到小波位移完整个信号 f ( t ) f(t) f(t)。

- 扩展小波的尺度,比如扩展一倍,小波函数变为 ψ ( t 2 ) \psi(\frac{t}{2}) ψ(2t)。然后重复步骤1~3。

- 重复步骤1~4直到小波已经拓展到规定的最大尺度。
进行完这五个步骤之后,我们就能够得到在不同的小波尺度和不同的信号位置上的小波系数了。如何更直观的理解这个系数呢?于是我们可以把 C ( a , b ) C(a,b) C(a,b)画出来,x轴代表信号的时间(或说小波位移的长度b);y轴表示尺度a;图中每个点的颜色浅深表示C(a,b)的大小。下面是一个系数图,其实在第一部分中也有我自己信号的CWT系数图,忘了的可以回去看一下。

当然也可以看系数图的侧面视角,图像如下:

回到文章主题,检测信号突变点上。如果信号存在突变点的话,总有一些小尺度的小波在经过突变点这个位置的时候,此时计算出的 C ( a , b ) C(a,b) C(a,b)会比周围的点都大。从系数图中我们可以想到这些位置会更亮一些,于是就找到了突变点。
2.2 离散小波变换(DWT)
f ( t ) f(t) f(t)的二进制连续小波变换为:
C ( 2 j , b ) = 1 2 j ∫ R f ( t ) ψ ∗ ( t − b 2 j ) d t (1) C(2^j,b) = \frac{1}{\sqrt{2^j}} \int_R f(t) \psi^*(\frac{t-b}{2^j})dt \tag{1} C(2j,b)=2j1∫Rf(t)ψ∗(2jt−b)dt(1)
当 b = k 2 j b=k2^j b=k2j,式(1)为离散小波变换;当 b = k b=k b=k,式(1)为平稳小波变换(二进小波变换)。
平稳小波变换只对尺度参数进行了离散化,而对时间域上的平移参数保持整数连续变化,平稳小波变换未破坏信号在时间域上的平移不变量。
DWT有多种实现方式,除了按照上述公式做的离散小波变换,其实还有一种更为常用的离散小波变换的方法,叫做Mallat算法,其实我们在第一部分将信号分成3层近似系数和细节系数就是用的这种方法。
2.2.1 半子带滤波
对于大多数信号来说,信号的低频部分是对信号整体特征的刻画;而高频部分则表现了信号的细枝末节。比如我们的声音,如果把声音的高频部分去去掉,虽然听起来有点不一样,但我们仍然能够听得出说的什么内容,但如果把足够多的低频分量去掉,那就完全不知道在说什么了。
在小波分析中,我们把信号的低频部分称之为近似系数A(Approximations),把信号的高频部分称作细节系数D(Details),于是我们可以通过一个半子带滤波器来得到A和D。
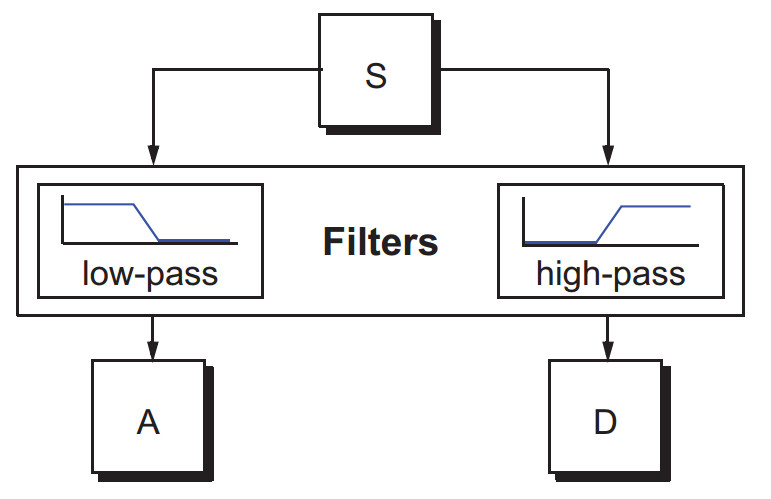
原始信号S,通过两个互补的滤波器,生成两个信号A和D。
值得注意的一点是,假设原始实数字信号S有1000个采样点的长度,那么经过滤波后,A和D分别都会有1000个点,它们加在一起有2000个点,就比S还长了。由于之后重构S的需要,现在我们使用下采样的方法将A和D各自降成500个点,方法是每两个点取一个点就好了。下采样之后的信号分别是cA1和cD1。

2.2.2 离散小波分解
在得到近似系数cA1之后,对cA1也进行半子带滤波加下采样,得到cA2和cD2,重复这个操作,可以最多进行 l o g 2 N log_2{N} log2N层小波分解。
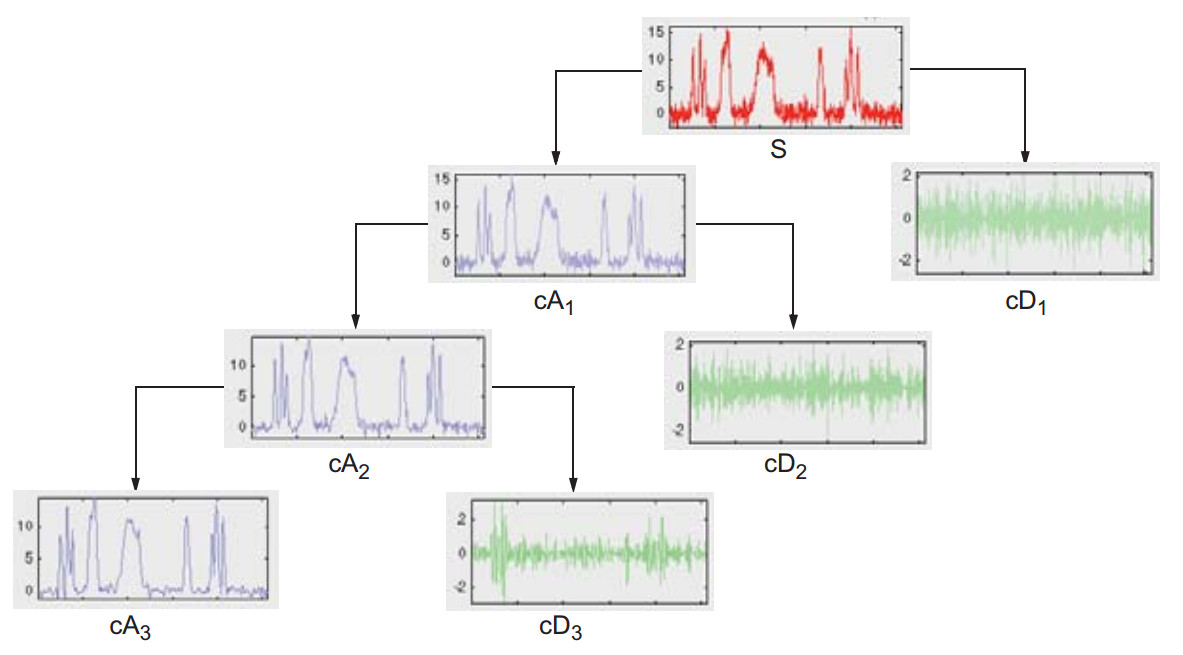




)







)
![[QCM6125][Android13] 默认关闭SELinux权限](http://pic.xiahunao.cn/[QCM6125][Android13] 默认关闭SELinux权限)


)


