1.这个多项式回归问题可以准确地解出吗?提⽰:使⽤线性代数。
可以,把多项式问题,用matlab的str2sym表示出来,再用solve求解。
2.考虑多项式的模型选择。
- 1. 绘制训练损失与模型复杂度(多项式的阶数)的关系图。观察到了什么?需要多少阶的多项式才能将训练损失减少到0?
画图代码(阶数1-100):
# 记得把max_degree改为100# 把train改成这个函数
def trainLossComplex(train_features,test_features,train_labels,test_labels,num_epochs=1000):loss=nn.MSELoss(reduction='none')input_shape=train_features.shape[-1]# 不设置偏置,因为我们已经在多项式中实现了它net = nn.Sequential(nn.Linear(input_shape,1,bias=False))batch_size=min(10,train_labels.shape[0])train_features=torch.tensor(train_features, dtype=torch.float32)test_features=torch.tensor(test_features, dtype=torch.float32)train_iter=d2l.load_array((train_features,train_labels.reshape(-1,1)),batch_size)test_iter=d2l.load_array((test_features,test_labels.reshape(-1,1)),batch_size,is_train=False)trainer=torch.optim.SGD(net.parameters(),lr=0.01)for epoch in range(num_epochs):d2l.train_epoch_ch3(net,train_iter,loss,trainer)return evaluate_loss(net,train_iter,loss),evaluate_loss(net,test_iter,loss)
trainLoss=[]
textLoss=[]
x=np.arange(1,100)
for i in np.arange(1,100):train_loss,text_loss=trainLossComplex(poly_features[:n_train, :i], poly_features[n_train:,:i],labels[:n_train],labels[n_train:])trainLoss.append(train_loss)textLoss.append(text_loss)
d2l.plot(x, y, xlabel='degree', ylabel='train_loss', legend=None, xlim=None,ylim=[1e-3+0.007,1*1e-2+0.005], xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None)
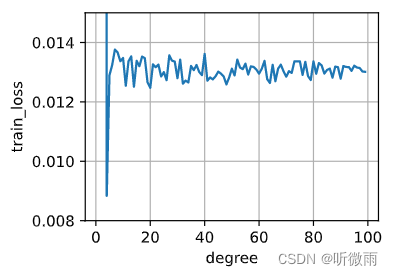
从图中看,1-100的阶数的多项式都不能把训练损失减少到0
- 2. 在这种情况下绘制测试的损失图。
d2l.plot(x, textLoss, xlabel='degree', ylabel='train_loss', legend=None, xlim=None,ylim=[1e-3,1.2], xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None)
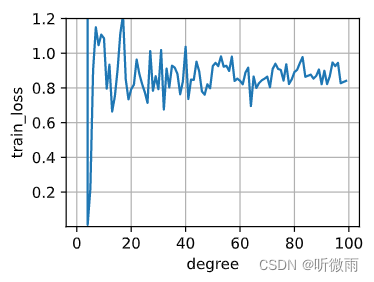
这里的值没有到0,只是图上看着到了
- 3. ⽣成同样的图,作为数据量的函数。
改一改数据量吧,再自己画一下吧,我太懒了,对不起
3. 如果不对多项式特征xi进⾏标准化(1/i!),会发⽣什么事情?能⽤其他⽅法解决这个问题吗?
如果有一个 x大于 1,那么这个很大的 i就会带来很大的值,优化的时候可能会带来很大的梯度值。
4. 泛化误差可能为零吗?
不太可能



)



 - 编译FISCO BCOS的过程监测)



)







