全世界只有3.14 % 的人关注了

爆炸吧知识

转自：量子位

作者：边策 萧箫

当两个看似“无关”的数学领域发生碰撞，会发生什么？

浙江大学研究员、中科大数学系2003级校友叶和溪，与来自剑桥大学、哈佛大学的两位学者一起，将动力系统应用到数论中，解开了困扰数学家长达数十年的难题。

研究成果发表在数学界顶级期刊《数学年刊》（Annals of Mathematics）上，该学术期刊为双月刊，近两年每年仅发表三十多篇学术论文。

这也是浙大40多年来首次在该期刊上发表成果。

叶和溪结合动力系统方法，证明了数论中一个非常重要的问题。

动力系统，主要研究空间中所有点随时间变化的情况。这门学科最著名的便是“蝴蝶效应”中的洛伦茨吸引子。

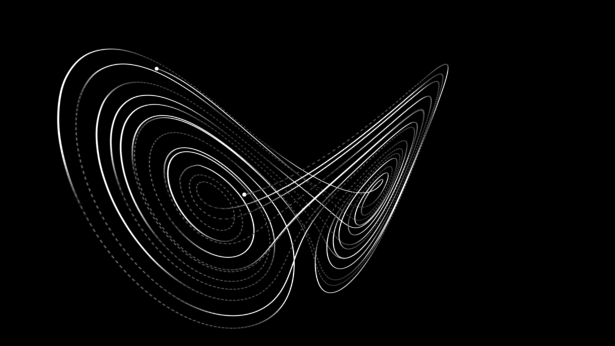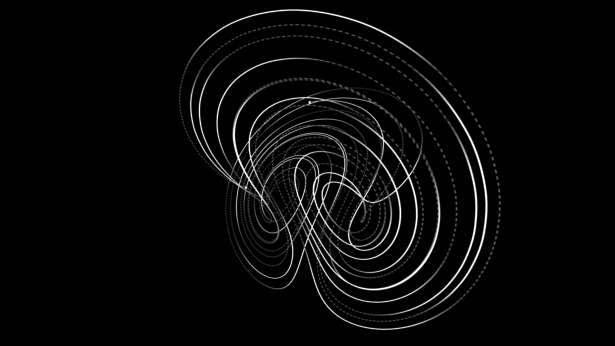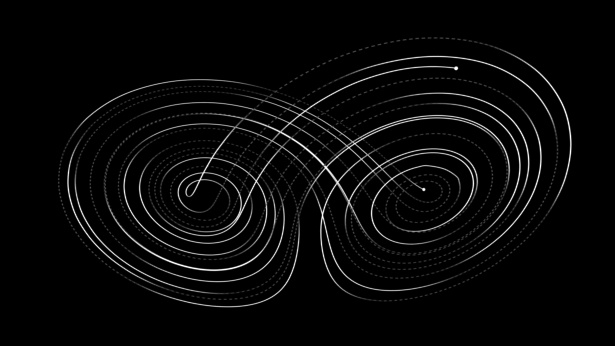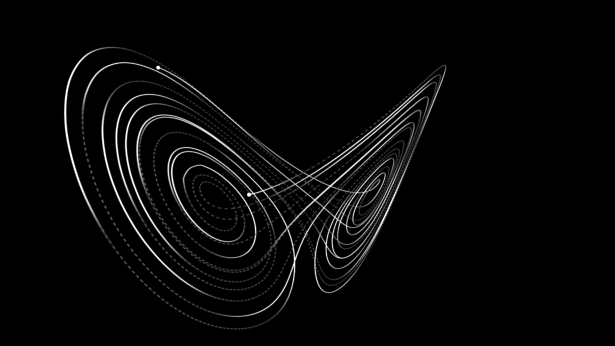
△洛伦茨吸引子

然而数论，研究的却是整数的性质。

这两个看起来风马牛不相及的领域，被数学家们巧妙地被结合到一起。

它们是怎么联系起来的，首先还得从两个方程说起。

两个方程

• 1、y²=x³+ax+b

• 2、f(z)=z²+c

第一个方程表示椭圆曲线，当a和b不断变化时，椭圆曲线形状各不相同，就像是从曲线中挤出一个“气泡”。

椭圆曲线是数论中的重要工具，数学家证明费马大定理就用到了它。

在椭圆曲线上，你甚至可以对两个点做加法。

假设有两个点P、Q，那么PQ连线与曲线的第三个交点R对x轴的镜像点，就是P+Q。R的镜像点记为-R，即-R=P+Q。

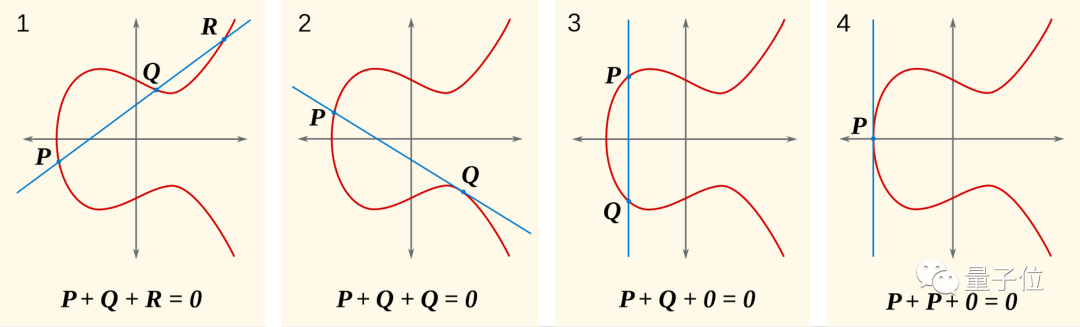
因为椭圆曲线是上下对称的，所以P+Q也一定在椭圆曲线上。

那么P点和它自己相加（P+P）怎么计算？

想象一下Q点越来越靠近P点，最后PQ两点的连线就变成P点处的切线，所以P+P就是这个切线与椭圆曲线交点的镜像点。

如果P点反复加上自己，经过有限次加法后（P+P+……+P）又回到P点，那么P就叫做“挠点”（torsion point）。

再看第二个方程数学公式: f(z)=z^2+c，它不是二次曲线，而是与另一门数学分支动力系统有关。

z在这里不是实数，而是实数+虚数。如果我们画出一个平面坐标，横坐标代表它的实数部分，纵坐标代表它的虚数部分，z就是一个点。

我们把z、f(z)两个点画在这个平面上，再把f(z)带入方程得到f(f(z))，然后再得到f(f(f(z)))……

如此“无限套娃”操作，把所有的点都画出来，可以得到以下图形。

有些人可能已经发现，这不就是分形吗，怎么和椭圆曲线联系起来了？

上面的图形范围有限，说明某些z值在经过无限套娃后，还是有限的数值。

假设c=-1，z的初始值为2，那么得到的数字组合是2、3、8、63……，这组数会一直增大；如果z的初始值是0，那么接来下的数分别是-1、0、-1、0……，会一直循环下去。

对于第二种情况，无限次迭代后的每个点都在有限范围内，这些有限范围内的点组成的集合，就是“朱利亚集合”（Julia set）。

在动力系统中，像-1、0、-1、0……这样，不仅范围有限，还能够回到起点的一组点，称为“有限轨道点”（finite orbit point）。

这样，椭圆曲线就和动力系统联系起来了，有限轨道点便是椭圆曲线上挠点的模拟。

叶和溪的导师DeMarco说：“椭圆曲线上的挠点与某个动力系统的有限轨道点相同，这就是我们在论文中反复使用的内容。”

证明数学猜想

但这三位数学家研究的问题——Manin-Mumford猜想——比上面复杂得多。

Manin-Mumford猜想是比椭圆曲线更复杂的曲线，例如y^2 = x^6 + x^4 + x^2 −1，每个不同参数的曲线都与一个几何体关联。

Manin-Mumford猜想于1983年被Raynaud证明，即亏格（genus）大于1的任意光滑代数曲线上至多只有有限个挠点。

对于封闭的有向曲面而言，亏格就是曲面的“洞”数量。

椭圆曲线对应的几何体是亏格为1的“甜甜圈”。

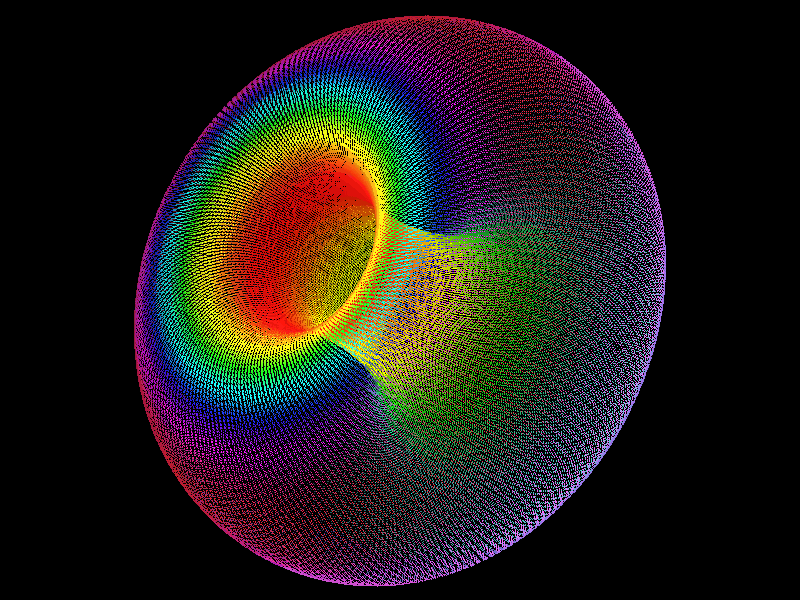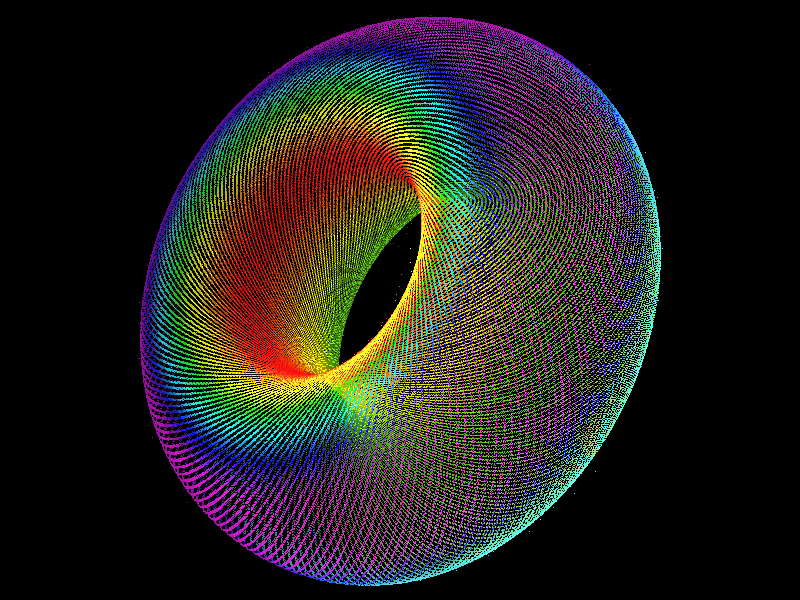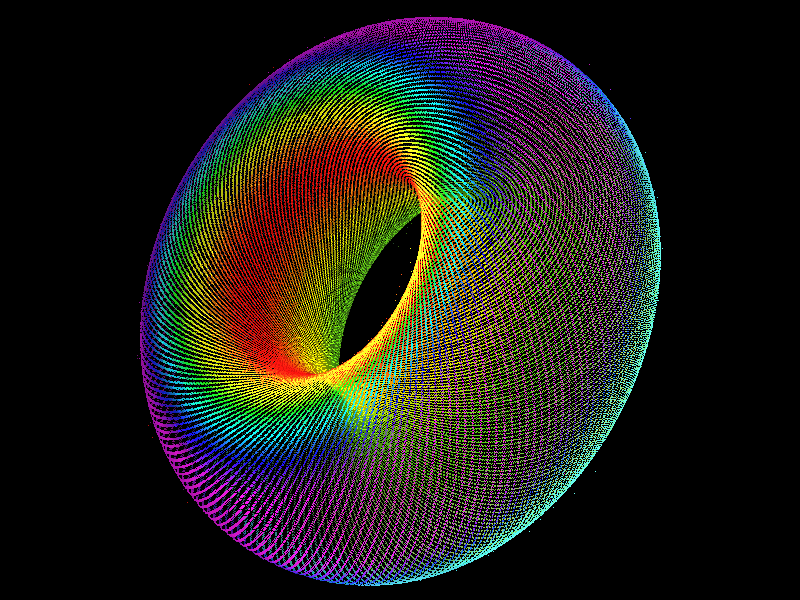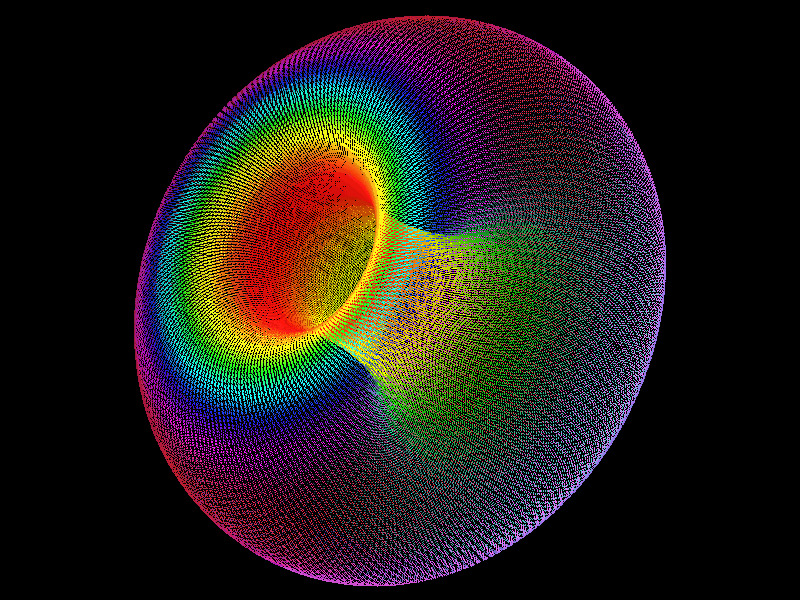
叶和溪等人将Manin-Mumford猜想又推进了一步，他与Holly Krieger、Laura DeMarco一起，结合动力系统证明了，在亏格为2的情况下，光滑代数曲线挠点数量不仅有限，而且具有一致上界。

与椭圆曲线不同的是，Manin-Mumford猜想中的复杂曲线不具备允许做加法的结构。

但是它们对应的几何体却都可以做加法，而且像椭圆曲线一样具有挠点。

他们给出了待求的特定曲线簇的解的形状：像是两个甜甜圈的表面（亏格为2）。

其中，每个“甜甜圈”代表一个椭圆曲线。

而要证明挠点数量的上限，就需要计算出椭圆曲线上挠点之间的相交点数量。

然而这两条椭圆曲线上的挠点不可能直接比较，因为它们不一定重叠。

几位学者想出了一种方法：比较它们是否在“甜甜圈”上各自处于相同的相对位置。

他们将两条椭圆曲线的解各自绘制在一张平面图上，以此来比较挠点的位置。

接下来，只需要计算这些点重叠的次数，就能给Manin-Mumford猜想一个明确的上界了。

这里，便是动力系统需要发挥作用的地方。

他们利用动力系统，证明了这些点只能重合特定的次数，而且这一次数确实存在——即Manin-Mumford猜想的上界确实存在。

对于他们的证明，来自加拿大约克大学的助理教授Patrick Ingram表示：

他们成功证明了一个特殊问题。此前，这个问题一直被归类于数论中，没人认为它与动力系统有关。这确实引起了极大的轰动。

与导师旧友一同解决重要猜想

事实上，猜想证明背后的三位学者，彼此也是导师与旧友的关系。

这其中，叶和溪与论文作者Holly Krieger，都曾经是Laura DeMarco的学生。

△Holly Krieger

2013年，他们在后者的指导下，获得了伊利诺伊大学芝加哥分校的博士学位。

在这之后，Laura DeMarco如今已是哈佛大学教授，而Holly Krieger也已经成为一名剑桥大学的数学讲师。

△Laura DeMarco

叶和溪则选择了回国，成为浙江大学的数学系研究员。

但这期间，他们并未停止共同研究的步伐。

2017年，叶和溪就曾与Laura DeMarco、Holly Krieger一起，研究了动力系统中有界高度的问题，成果于2019年发表。

而在2019年，继证明Manin-Mumford一致猜想之后，他们也对动力系统中的另一个问题进行了深入探讨，并采用了类似的研究方法。

目前，这篇文章以预印本的形式发表。

2020年4月15日，他们证明的Manin-Mumford一致猜想，最终成功刊登在《数学年刊》上。

中科大03级数学人才“井喷”

在这次研究中做出不少贡献、来自浙江大学的研究员叶和溪，高中曾就读于福建省建瓯第一中学。

2003年，叶和溪进入中国科学技术大学数学系学习。

△ 图源：公众号@中国科大本科招生

本科毕业后，叶和溪选择出国深造，研究方向就是数学中的动力系统。

2013年，他在导师Laura DeMarco的指导下，完成了博士学位，毕业于伊利诺伊大学芝加哥分校。

在这之后，他曾经先后在多伦多大学、英属哥伦比亚大学从事博士后研究工作。

完成学术研究后，叶和溪于2016年回国任教。

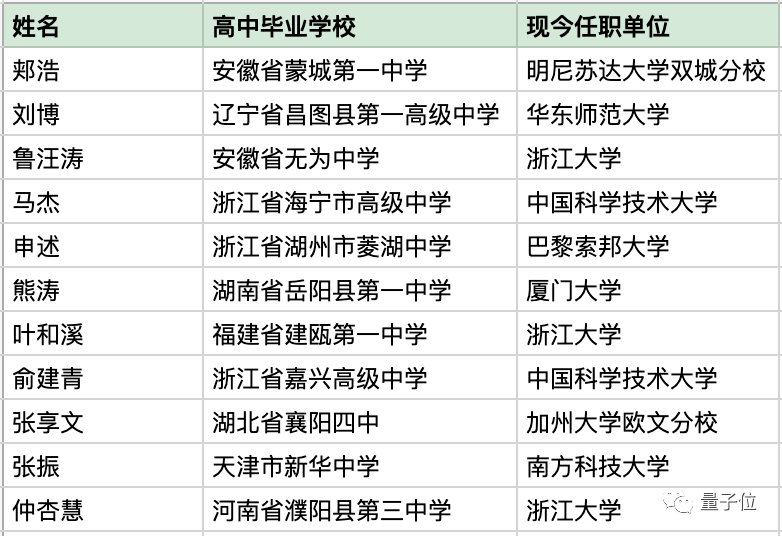
与叶和溪一同入学的中科大数学系校友，也是人才辈出。

其中，至少5位学者的研究，再世界“四大数学顶刊”上发表过论文。

叶和溪同班同学郏浩、刘博、申述、张享文，也都已经在《数学发明》上各发表一篇论文。

还有许多与叶和溪、刘博一样学成归来的学子，如鲁汪涛、马杰、熊涛、张振、仲杏惠等中科大校友，毅然决然地放弃了国外的条件，回到国内继续从事数学研究。

△ 图源：公众号@中国科大本科招生

对于2003级学子在数学上取得的成就，中国科学院院士、南开大学陈省身数学研究所张伟平由衷地表示自豪：

事实证明，科大的学生不管考第几，到哪里都是一块好料。在同一个班就有这么多杰出的人才涌现，殊为罕见。

本文转自量子位

作者：边策 萧箫

论文地址：
https://arxiv.org/abs/1901.09945

参考链接：

[1]

https://www.quantamagazine.org/with-arithmetic-dynamics-mathematicians-unlock-new-insights-20210222/ 
[2] http://www.math.zju.edu.cn/2020/0422/c38119a2087975/page.htm
[3] https://mp.weixin.qq.com/s/m0iFwivlfmSDKdfltR_Flw 
[4] 

https://docs.google.com/viewer?a=v&pid=sites&srcid=ZGVmYXVsdGRvbWFpbnx5ZWhleGltYXRofGd4OjQ3ZjkzYjc5YjcwNTYxOTA 
[5] https://arxiv.org/abs/1511.06081

点这里????关注我，记得标星～