asp 强制转换浮点数值_C/C++中浮点数的编码存储

浮点数也称做实型数据(实数)，形式上就是数学中的小数。浮点型数据有两种表达方式：一种是用数字和小数点表示的，如123.456；另一种是用指数方式表示，如1.2e-6 或1.2E-6(1.2*10-6)。

在计算机中实数是如何存储的呢？主要分为定点实数存储方式和浮点实数存储方式这两种。所谓定点实数，就是约定整数位和小数位的长度，比如用4字节存储实数，我们可以让高两个字节存放整数部分，低两个字节存储小数部分。这样的好处是计算的效率高，缺点是如果我们想存储65536.5，由于整数的表达范围超过了两个字节，用定点存储的方式就无法存储了。

对应地，也有浮点实数存储方式，就是用一部分二进制位存放小数点的位置信息，我们可以称之为”指数域”,其他的数据位用来存储没有小数点的数据和符号，我们可以称之为“数据域”、“符号域”。在访问时取得指数域，与数据域运算后得到真值，如67.625，利用浮点实数存储方式，数据域可以记录为67625，小数点的位置可以记录为10的-3次方。后来引进了浮点协处理器(FPU)，专门负责对浮点数的处理，使得对处理实数的效率大大提高，于是浮点实数存储方式也就普及开来，成为了现在主流的实数存储方式。

在C/C++中，使用浮点方式存储实数，用两种数据类型来保存浮点数：float(单精度)和double(双精度)。Float在内存中占用4字节空间，double在内存中占用8个字节空间。Double类型比float类型精度更高。这两种数据在内存中都是以十六进制方式存储，但与整型数据有所不同。

整型数据是将十进制直接转换成二进制保存在内存中，以十六进制方式显示。而浮点类型不是将一个浮点小数直接转换成二进制保存，而是将浮点小数转换成二进制码后重新编码，再进行存储。C/c++的浮点数是有符号的。

在C/C++中，将浮点数强制转换成整数时，不会采用数学上的四舍五入方式，而是舍弃掉小数部分。

浮点数的操作不会用到通用寄存器，而是用浮点协处理器的浮点寄存器。

浮点数的编码方式

浮点编码转换采用的是IEEE规定的编码标准，float和double这两种类型数据的转换原理相同，但由于表示的范围不一样，编码方式有些区别。IEEE规定的浮点数编码会将一个浮点数转换为二进制数。以科学计数法划分，将浮点数拆分为3个部分：符号、指数和尾数。

1、float类型的IEEE编码

Float类型在内存中占4个字节(32位)。最高位表示符号：在剩余的31位中，从右到左取8位用于表示指数，其余用于表示尾数。如图2-2所示：

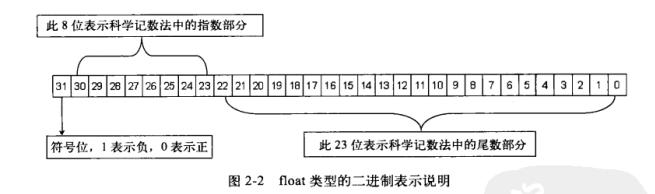
float类型的IEEE编码

1)在进行二进制转换前，需要对单精度(float)浮点数进行科学计数法转换。例如，将float类型的12.25f(f表示为float单精度类型)转换为IEEE编码，需要将12.25f转换成对应的二进制数1100.01，整数部分为1100，小数部分为01。小数点向左移动，每移动1次指数加1，移动到除了符号位的最高位1处，停止移动。这里移动3次。对12.25f进行科学记数法转换后的二进制部分为1.10001，指数部分为3。在IEEE编码中，由于在二进制情况下，最高位始终为1，为一个恒定值，故将其忽略不计。这里是一个正数，所以符号位添0。

12.25f经过IEEE转换后各位的情况：

符号位：0

指数为：十进制 3+127，转换为二进制10000010

尾数位：10001 000000000000000000(当不足23位时，低位补0填充)

由于尾数位中最高位1是恒定值，故省略不计，只要在转换回十进制时加1即可。为什么指数位要加127呢？由于指数可能出现负数，十进制127 可表示二进制数 01111111。IEEE编码方式规定，当指数域小于0111111时为一个负数，反之为正数，因此指数域加上十进制数 127 表示正数。

12.25f转换后的IEEE编码按二进制拼接为 0 10000010 10001000000000000000000。转换后成十六进制数 0x41440000，内存中以小端进行存储，故为 00 00 44 41。分析结果如图所示：

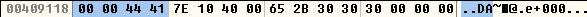
2)上面演示了符号位为正，指数为也为正的情况。那么什么情况下指数位可以为负呢？根据科学记数法，小数点向整数部分移动时，指数做加法。相反，小数点向小数部分移动时，指数需要以0起始做减法。浮点数 -0.125f转换成IEEE编码后，将会是一个符号位为1，指数部分为负的小数。-0.125f经转换后二进制部分为0.001，用科学记数法为1.0，指数为-3。

-0.125f 经过IEEE转码后各位的情况为：

符号位：1

指数位：十进制127+(-3)，转换为二进制是 01111100，如果不足8位，则高位补0

尾数位：0000000000000000000000000

-0.125f经转换后的IEEE编码二进制拼接为 1 01111100 0000000000000000000000000。转换后成十六进制为 0xBE000000，内存中显示为 00 00 00 BE。分析结果如图所示：

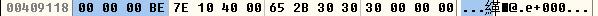
3)上面的两个浮点小数部分转换为二进制时都是有穷的，如果小数部分转换为二进制时得到一个无穷值，则会根据尾数部分的长度舍弃多余的部分。单精度浮点数1.3f，小数部分转换为二进制就会产生无穷值，依次转换为0.3、0.6、1.2、0.4、0.8、1.6、1.2、0.4、0.8...，转换后得到的二进制数位1.01001100110011001100110，到第23为时终止，尾数部分无法再保存。

1.3f经过IEEE转换后各位的情况：

符号位：0

指数位：十进制0+127，转换二进制01111111

尾数位：01001100110011001100110

1.3f 转换后的IEEE编码二进制拼接为 0 01111111 01001100110011001100110。转换成十六进制数位 0x3fa66666，内存中显示为 66 66 a6 3f。由于在转换二进制过程中产生了无穷值，舍弃了部分位数，所以进行IEEE编码转换后得到的是一个近似值，存在一定的误差。再将这个IEEE编码值转换成十进制小数，得到的值为1.2516582，四舍五入后为1.3.这也解释了为什么C++ 在比较浮点数值是否为0时，要做一个区间而不是直接进行等值比较。如：

float fTemp = 0.0001f; // 精确范围

if (fFloat >= -fTemp && fFloat <= fTemp)

{

fTemp等于0

}

2.double类型的IEEE编码

前文讲解了单精度浮点类型的IEEE编码。Double类型和float类型大同小异，只是double类型表示的范围更大，占用空间更多，精度更准。

Double 类型占8字节的内存空间，同样最高位也用于表示符号，指数位占11位，剩余的52位用于表示尾数。

在float中，指数位范围用8位表示，加127后用于判断指数符号。在double中，由于扩大了精度，因此指数范围使用11位正数来表示，加上1023来用于指数符号判断。

Double 类型的IEEE编码转换过程和float一样。

3.浮点数指令

浮点数的操作指令和普通数据类型不同，浮点数操作是通过浮点寄存器来实现的，而普通数据使用的是通用寄存器，如eax、edx、ebx等。

浮点寄存器是通过栈结构来实现的，由ST(0)~ST(7)共8个栈空间组成，每个浮点寄存器占8个字节。每次使用浮点寄存器都是先使用St(0),而不能越过ST(0)直接使用ST(1)。浮点寄存器的使用就是压栈、出栈的过程。当ST(0)存在数据时，执行压栈操作，ST(0)中的数据将进入到ST(1)中，如无出栈操作，将顺序地向下压栈，直到将浮点寄存器占满。常用浮点数指令如下所示：IN 表示操作数入栈。OUT表示操作数出栈。

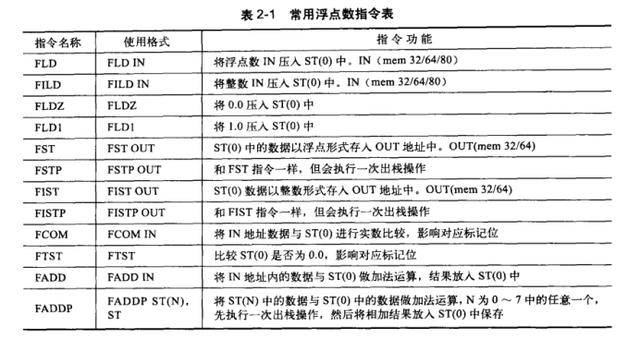
常用浮点数指令

其他运算指令和普通指令类似，只需在前面加F就行，如 FSUB和FSUBP等。

在使用浮点指令时，都要先利用ST(0)进行运算。当ST(0)中有值时，便会将ST(0)中的数据顺序向下存放到ST(1)中，然后再将数据放入ST(0)中。如果再次操作ST(0)，则会先将ST(1)中的数据放入ST(2)中，然后将ST(0)中的数据放入到ST(1)中，最后才将新的数据存放到ST(0)。以此类推，在八个浮点寄存器都有值的情况下继续向ST(0)存放数据，这时会丢弃ST(7)中的数据信息。

1)下面通过一个简单的例子来了解各个指令的使用流程：

// 浮点数使用

float fFloat = (float)argc;

00401028 fild dword ptr [ebp+8]

//将ebp+8处的整型数据转换成浮点型，并放入ST(0)中，对应变量 argc

0040102B fst dword ptr [ebp-4]

//从ST(0) 中取出数据以浮点编码的方式放入地址ebp-4 中，对应变量 fFloat

printf("%f", fFloat);

0040102E sub esp,8

//这里对esp减 8 操作是由于浮点数作为变参函数的参数时需要转换成双精度浮点值,

//这步操作是提前准备8字节的栈空间，以便存放double数据。

00401031 fstp qword ptr [esp]

//将ST(0) 中的数据传入esp中，并弹出ST(0)。

00401034 push offset string "%f" (00426020)

00401039 call printf (00401420)

0040103E add esp,0Ch

argc = (int)fFloat;

//将 float类型数据转换成int型

00401041 fld dword ptr [ebp-4]

//将ebp-4处的数据以浮点型压入ST(0)中。

00401044 call __ftol (00401588)

//调用函数 __ftol 进行浮点数转换， __ftol的实现见下文。

00401049 mov dword ptr [ebp+8],eax

printf("%d", argc);

0040104C mov eax,dword ptr [ebp+8]

0040104F push eax

00401050 push offset string "%d" (0042601c)

00401055 call printf (00401420)

0040105A add esp,8

从上面示例中可以发现，float类型的浮点数虽然占4个字节，但都是以8个字节(qword)方式进行处理。当浮点数作为参数时，并不能直接压栈。Push 指令只能传入4字节数据到栈中，这样会丢失4字节数据。这就是为什么使用printf函数以整型方式输出浮点数会产生错误的原因。Printf以整数方式输出时，将对应参数作为4字节数据，按补码方式解释。而真正压入的参数为浮点类型时，数据长度为8字节，需要按浮点编码解释。

2)浮点数作为返回值的情况也是如此，同样需要传递8字节数据，代码如下所示：

float fFloat;

fFloat = GetFloat();

00401058 call @ILT+5(_GetFloat) (0040100a)

//调用GetFloat函数

0040105D fst dword ptr [ebp-4]

//由于浮点数需要特殊处理，浮点数占8个字节，无法使用EAX进行传递

//因此使用浮点寄存器 ST(0) 作为返回值

printf("%f", fFloat);

00401060 sub esp,8

00401063 fstp qword ptr [esp]

00401066 push offset string "%f" (00426020)