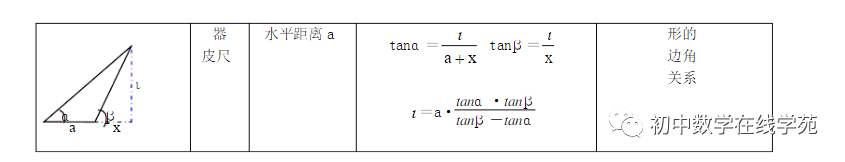
考点一、直角三角形的性质  

1、直角三角形的两个锐角互余：可表示如下：∠C=90°∠A+∠B=90°

2、在直角三角形中，30°角所对的直角边等于斜边的一半。

3、直角三角形斜边上的中线等于斜边的一半

4、勾股定理： 如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a²＋b²＝c². 即直角三角形两直角边的平方和等于斜边的平方

勾：直角三角形较短的直角边     股：直角三角形较长的直角边      弦：斜边

勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a²＋b²＝c²，那么这个三角形是直角三角形。

考点二、直角三角形的判定

1、有一个角是直角的三角形是直角三角形、有两个角互余的三角形是直角三角形

2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

3、勾股定理的逆定理：如果三角形的三边长a、b、c满足a²+b²=c² ，那么这个三角形是直角三角形。(经典直角三角形：勾三、股四、弦五)

用它判断三角形是否为直角三角形的一般步骤是：

(1)确定最大边(不妨设为c)；

(2)若c²＝a²＋b²，则△ABC是以∠C为直角的三角形；

若a²＋b²＜c²，则此三角形为钝角三角形(其中c为最大边)；

若a²＋b²＞c²，则此三角形为锐角三角形(其中c为最大边)

4.勾股定理的作用：

    (1)已知直角三角形的两边求第三边。

    (2)已知直角三角形的一边，求另两边的关系。

(3)用于证明线段平方关系的问题。

(4)利用勾股定理，作出长为的线段

考点三、锐角三角函数的概念

1、如图，在△ABC中，∠C=90°

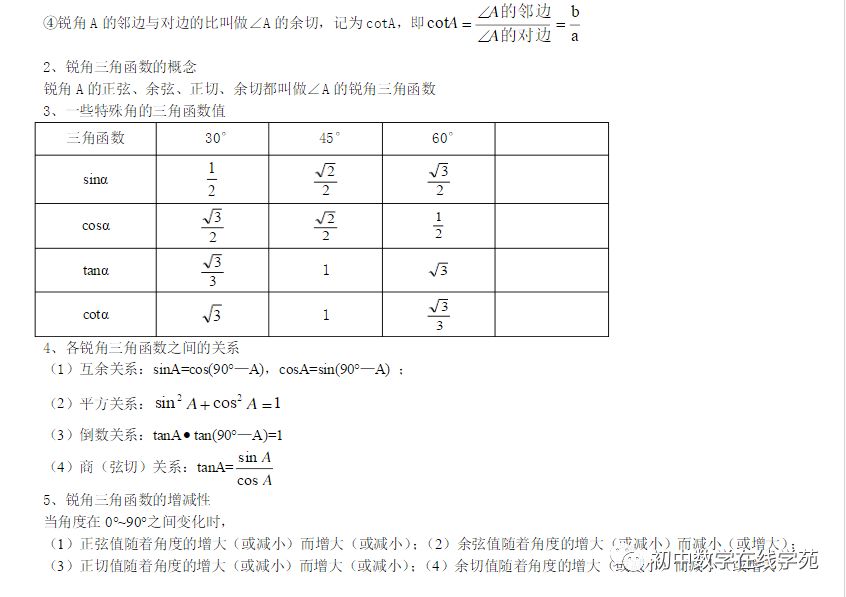
①锐角A的对边与斜边的比叫做∠A的正弦，记为sinA，即

②锐角A的邻边与斜边的比叫做∠A的余弦，记为cosA，即

③锐角A的对边与邻边的比叫做∠A的正切，记为tanA，即

④锐角A的邻边与对边的比叫做∠A的余切，记为cotA，即

2、锐角三角函数的概念

锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数

3、一些特殊角的三角函数值

4、各锐角三角函数之间的关系

(1)互余关系：sinA=cos(90°—A)，cosA=sin(90°—A) ；

(2)平方关系：

(3)倒数关系：tanAtan(90°—A)=1

(4)商(弦切)关系：tanA=

5、锐角三角函数的增减性

当角度在0°~90°之间变化时，

(1)正弦值随着角度的增大(或减小)而增大(或减小)；(2)余弦值随着角度的增大(或减小)而减小(或增大)；(3)正切值随着角度的增大(或减小)而增大(或减小)；(4)余切值随着角度的增大(或减小)而减小(或增大)

考点四、解直角三角形   

1、解直角三角形的概念

在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。

2、解直角三角形的理论依据

在Rt△ABC中，∠C=90°，∠A，∠B，∠C所对的边分别为a，b，c

(1)三边之间的关系：(勾股定理)

(2)锐角之间的关系：∠A+∠B=90°

(3)边角之间的关系：正弦sin，余弦cos，正切tan

(4) 面积公式：  (hc为c边上的高)

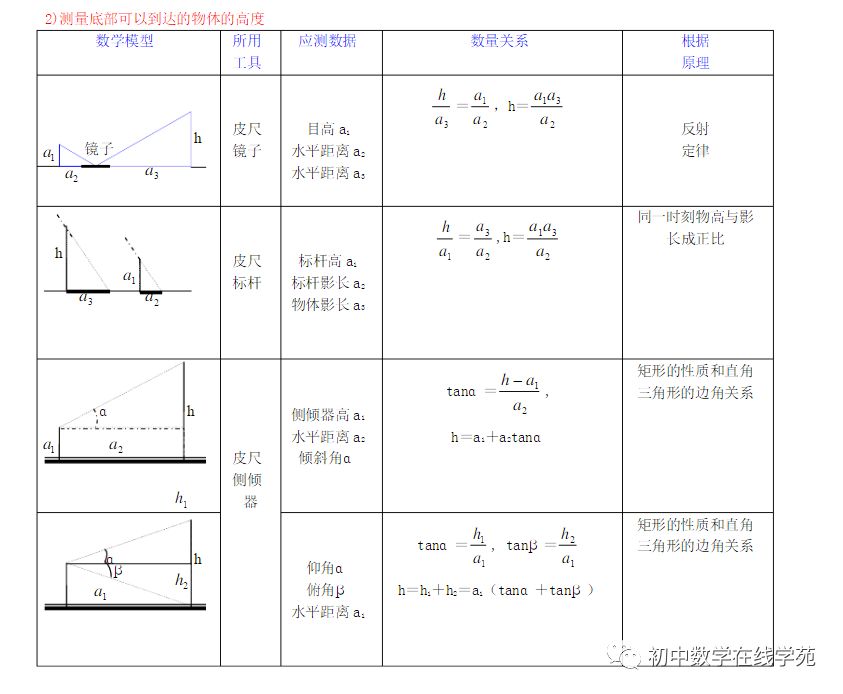
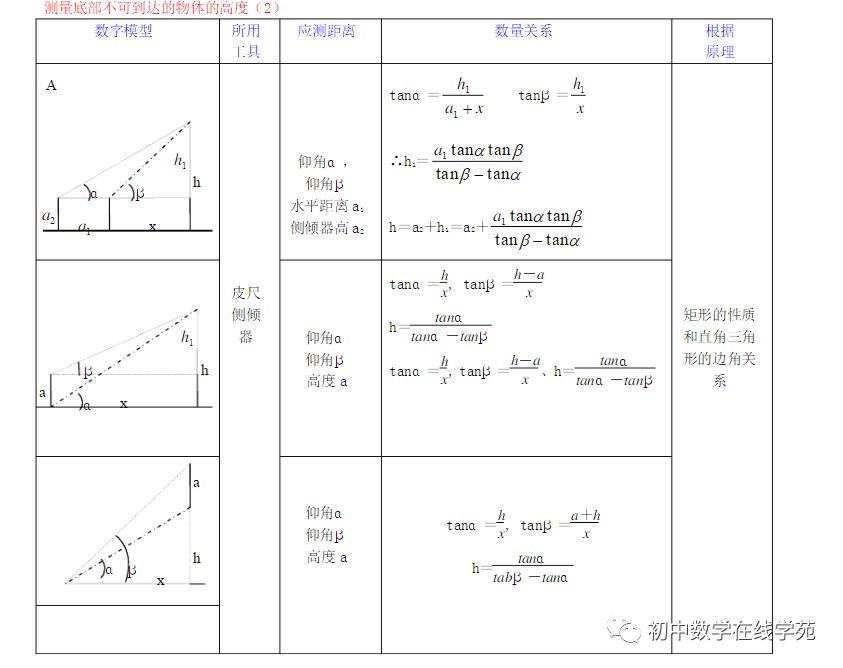
考点五、解直角三角形 应用

1、将实际问题转化到直角三角形中，用锐角三角函数、代数和几何知识综合求解

2、仰角、俯角、坡面 知识点及应用举例：

(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

(2)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。用字母表示，即。坡度一般写成的形式，如等。  把坡面与水平面的夹角记作(叫做坡角)，那么。

3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。如图3，OA、OB、OC、OD的方向角分别是：45°、135°、225°。