
主成分分析
主成分分析(PCA)是数据降维的一种常见方法,其它常见的方法还有因子分析(FA),独立成分分析,在进行大数据处理时,因为数据有很多特征,维数过高,不容易进行处理且不能进行可视化,所以一般要对其进行降维,我们都知道在二维平面中的两个点能确定一条直线,在三维平面中,三个点一定能确定一个平面,二维中的直线通过旋转变换可以转化到一个坐标上(一位数据),三维中的平面可以通过旋转转化到一个坐标平面上(二维数据),所以可以说这些确定直线和平面的点直接存在一定的相关关系,且可以通过某种关系将紧密关系的数据转化为经可能少的新变量。主成分分析就是利用这一点。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征[1],那么如何才能找到这样一组有正交特征的k维数据呢,在主成分分析技术中的思路是在原始坐标轴上顺序的找相互正交的坐标轴,寻找原则是:第一个新坐标轴的方向是始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴。那么如何才能得到最大差异性的主成分方向呢,就是对n维数据求协方差矩阵,在求出协方差矩阵的特征值和特征向量,选择最大的k个特征值对应的k个特征向量组成转移矩阵,和原始数据相乘得到新的数据。因为求特征值和忒特征向量有两种方式,特征值分解和奇异值分解。所以可以分两种方式进行主成分分析。
特征值分解
介绍特征值分解之前必须先知道矩阵乘法的集合意义,向量与矩阵相乘就是将向量进行旋转和伸缩(对线性变换不太了解的可以观看3Blue1Brown的视频分析,里面很形象的讲解了线性变换的过程),如果矩阵对某些向量只发生伸缩变换,不产生旋转效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值[2]。特征分解的公式如下:
其中
其中
奇异值分解
奇异值分解可以分解
其中
主成分分析执行步骤
1.首先需要对原始数据进行处理,将原始数据进行单位化,单位化是按特征进行的求出特征的样本方差,每个样本再除上对应的样本方差。样本方差求法如下:
2.去平均值(即去中心化),即每一位特征减去各自的平均值。
3.计算协方差矩阵
注意协方差的计算,协方差的计算是按照维度来计算的,即特征,如有矩阵329*9阶,一行表示一个样本供329个样本,每列表示一个特征,上式中,n=329,
具体解法可参考下面的matlab代码:
x=round(rand(10,3)*50);
function Z=pca_test(x)my_mean=mean(x,1);[m,n]=size(x);Z=zeros(n,n);for i=1:nfor j=1:nZ(i,j)=sum((x(:,i)-my_mean(i)).*(x(:,j)-my_mean(j)))/(m-1); endend
end
%输出的Z为协方差,这里是10*3阶矩阵,所以协方差为3*3阶4.计算协方差矩阵的特征值和特征向量(特征值和特征向量)
5.选取择最大的k个特征值对应的k个特征向量组成转移矩阵P,和原始数据X相乘得到新的数据Y。 Y=P*X。
matlab实现主成分分析
在matlab中有自带的求解pca(主成分分析)的函数pca()[3],函数的主要输入是经过单位化的原始数据,去中心化和计算协方差矩阵等步骤都在函数中实现,pca函数还有几个输入参数,但都是可选的(有默认值),如选择计算主成分分析的方式(特征值分解或奇异值分解)等。输出的主要有6个量:
coeff : 主成分系数 应该就是协方差矩阵的特征向量矩阵(也就是映射矩阵).完整输出的情况下是一个p-by-p 的matrix.每一列都是一个特征向量.按对应的特征值 的大小,从大到小进行排列。
score: 进行旋转(也就是利用映射矩阵coeff进行)后的结果i.e. score = X * coeff. n-by-p matrix这里有个坑 如果你使用pca时使用的是默认的中心化(i.e 不对'Centered'设置'false'),拿X *coeff 和score对比的时候, 记得把X中心化后再乘以coeff,之后再和score对比....;同样如果pca使用的是默认值, 恢复的X = score * coeff' (注意转置)是中心化后的数据。
latent: 主成分方差 也就是各特征向量对应的特征值,从大到小进行排列。
tsquared :()。
explained : 每一个主成分所贡献的比例,可以更直观的选择所需要降维的维数了,不用再用特征值去求了。
mu: X 按列的均值,当前仅当 'Centered'置于'true'(默认值)时才会返回此变量。
matlab代码
这里以matlab自带的数据进行仿真说明[4]:
load cities
%得到三个数据集
%ratings 329*9每一行表示一个样本,每一列表示一个特征。
%单位化样本数据
std_ratings=std(ratings);%std()函数是对ratings求样本方差,默认是按列求,求出的结果为1*9数组
one_ratings=ratings./(std_ratings);
%使用pca函数降维
[coeff,score,latent,tsquare,explained,mu]= pca(one_ratings);
%计算选取前k个特征值进行降维后和原数据的准确率
rate=cumsum(latent)./sum(latent);%cumsum是累加和函数
%计算后选取前面7个特征值可获得90%以上的准确率,将329*9的数据降维到329*7
%选取coeff特征向量的前7列。
cho=coeff(:,1:7)
new_ratings=ratings*cho;原数据乘上特征向量得到降维后的数据cities:它使用了衡量美国329个城市生活质量的9个指标:气候、住房、健康、犯罪率、交通、教育、艺术、娱乐和经济。对于各指标,越高表示越好,如高的犯罪指标表示低的犯罪率。它由三个数据集组成,categories是9个特征的字符说明,names是每个样本城市的字符名称,ratings才是我们需要关注的数组。
std():std函数总共有三个输入参数,其中有两个可选参数[5],flag--标注求样本方差时是除以n还是n-1,flag=0是除以n-1,flag=1是除以n,dim--表示是按列求还是按行求,dim=1是按照列分dim=2是按照行分 若是三维的矩阵,dim=3就按照第三维来分数据。默认情况下,flag=0,dim=1。
Microstrong:主成分分析(PCA)原理详解zhuanlan.zhihu.com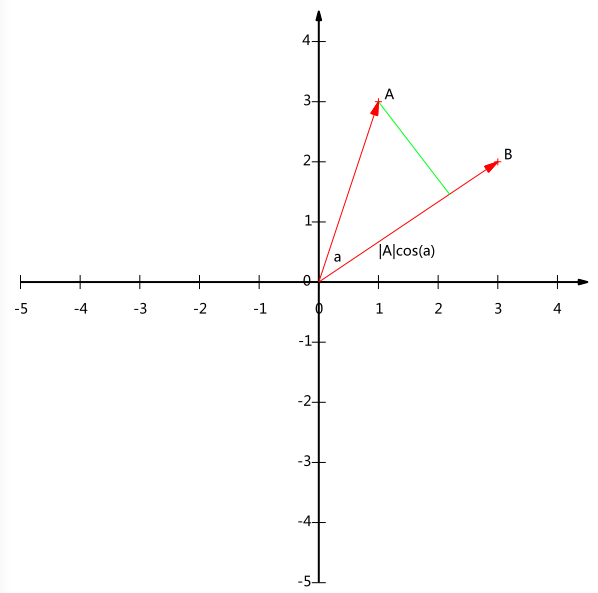
参考
- ^https://zhuanlan.zhihu.com/p/37777074
- ^特征值分解、奇异值分解、PCA概念整理 https://blog.csdn.net/jinshengtao/article/details/18448355
- ^https://blog.csdn.net/qq_25800311/article/details/83385029
- ^https://blog.csdn.net/ckzhb/article/details/75281727
- ^https://blog.csdn.net/qinze5857/article/details/79156555
)




C语言的变量、常量及运算)
 – 实现页面UI)




轻轻松松了解C语言的逻辑运算)





C语言的循环分分钟上手)

