cascade rcnn论文总结

1.bouding box regression总结：

　　rcnn使用l2-loss

　　首先明确l2-loss的计算规则：

　　　　　　　　　　　　　　　L∗=(f∗(P)−G∗)2，∗代表x,y,w,h

　　　　　　　　　　　　　　   整个loss : L=Lx+Ly+Lw+Lh

　　　　　　　　　　　　　　　也就是说，按照l2-loss的公式分别计算x,y,w,h的loss，然后把4个loss相加就得到总的bouding box regression的loss。这样的loss是直接预测bbox的

　　　　　　　　　　　　　　　绝对坐标与绝对长宽。

　　改进1:

　　　　  问题：如果直接使用上面的l2-loss，loss的大小会收到图片的大小影响。

　　　　  解决方案：loss上进行规范化(normalization)处理。

　　　　　　　　　  Lx=(fx(P)−Gx)W)2，Ly=(fy(P)−Gy)H)2，Lw=(fw(P)−Gw)W)2，Lh=(fh(P)−Gh)H)2，其中, W,H分别为输入图片的宽与高

　　　　  这种改进没有被采纳

　　改进2:

　　　　  rcnn直接使用的是下面这个公式，也使用了规范化，但除以的是proposal的wh，并且wh的loss用的log函数

　　　　 

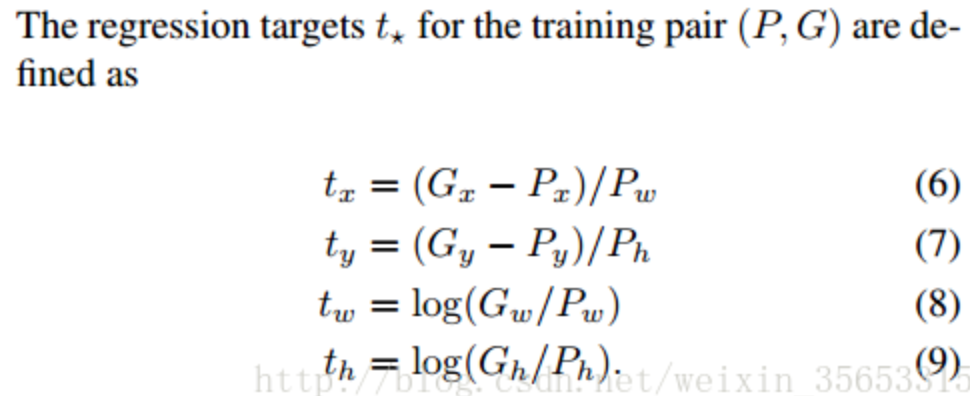
　　　　  cascade论文说这个改进的目的是：“To encourage a regression invariant to scale and location”，也就是增加scale和location的不变性　　 

　　　　  位置不变性：delta_x = [(g_x + a) - (b_x + a)] / b_w。不管平移量a是多少，delta_x都是一样的

  　　　　尺寸不变性：delta_w = log((g_w * b) / (b_w * b))。不管图片缩放b是多少，delta_w都是一样的

　  　　　至于为什么用log，有个博客说是：是为了降低w,hw,h产生的loss的数量级, 让它在loss里占的比重小些。  这个解释还有待观察

　　改进3:

　　　　  问题：当预测值与目标值相差很大时, 梯度容易爆炸, 因为梯度里包含了x−t

　　　　  解决方案：smoothl1代替l2-loss，当差值太大时, 原先L2梯度里的x−t被替换成了±1, 这样就避免了梯度爆炸

　　改进4:

　　　　  问题：由于bouding box regression经常只在proposal上做微小的改变，导致bouding box regression的loss比较小，所以bouding box regression的loss一般比classification

　　　　　　　  的loss小很多。（整个loss是一个multi-task learning，也就是分类和回归）

　　　　  解决方案：标准化

　　　　　　　　　  

 

延伸问题：iou-loss与l2-loss，smoothl1的优缺点

https://blog.csdn.net/weixin_35653315/article/details/54571681

 

2.性能上iou0.6大于iou0.5，但iou0.7却小于0.5，为什么？

0.7的iou生成的正样本的框的质量更高，应该性能更好，但ap值却在下降。原因在于，iou在0.5时，正样本大多集中在0.5到0.6之间，如果你阈值选在0.7，正样本数量大大减少，造成了过拟合。

3.iterative bbox多次做bouding box的回归，但每次回归都使用的iou0.5，没有考虑样本分布改变；integral loss是根据不同iou分别算loss，没有解决不同iou 正样本的数量不一样。cascade-rcnn与iterative bbox区别：1.每个stage进行了重采样   2.训练和测试的分布是一样的

因此cascade的好处是：1.不会出现过拟合。每一个stage都有足够的正样本

　　　　　　　　　　  2.每个stage用了更高的iou进行优化，proposal质量更高了

　　　　　　　　　　  3.高iou过滤了一些outliers

4.对比实验中的stat：就是为了解决分类loss大，bouding box regression loss小，将delta标准化的操作。

　　　　　　　　　  cascade rcnn中的stat是每一次回归都要做一次标准化，应该是因为每一次回归生成的新分布的均值和方差发生变化

5.对比实验1:

　　　　　

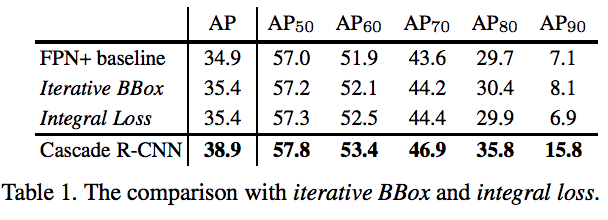
　　越高iou，cascade-rcnn提升越明显，最常用的ap50的提升最小且提升性能有限

　　延伸问题1： 为什么iou越低的检测性能会越低？

　　延伸问题2:   怎么去解决？

　　　　　　

  对比实验2:

　　　　　 

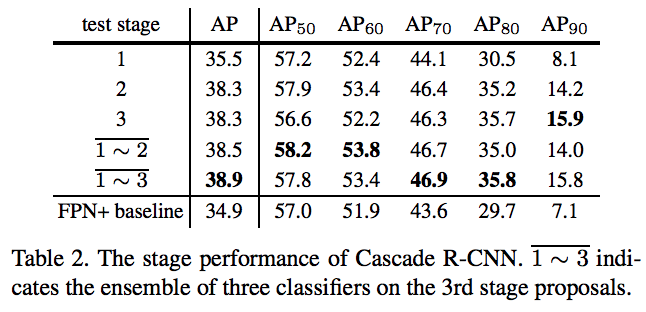
　　　　前提：这个实验是都用训练的时候用cascade rcnn，测试的时候在不同层测试和联合测试做对比。

　　　　a.单独在stage1上测试，性能比baseline要好，这是cascade的方式带来的提升；单独在stage2上测试性能提升最大，单独stage3在ap70以下有略微下降，以上有略微上升

　　　　b.在stage1、stage2上联合测试，ap70以下都获得了最好的结果，ap70以上会比stage3低一点；在stage1、stage2、stage3上联合测试，整体ap更高，ap70以上都有很大提升

　　　　

　　　　延伸问题1: 为什么出现这样的现象？

　　　　延伸问题2: cascade-rcnn如何做联合测试的？　　　　　 

 

对比实验3:

　　　　　

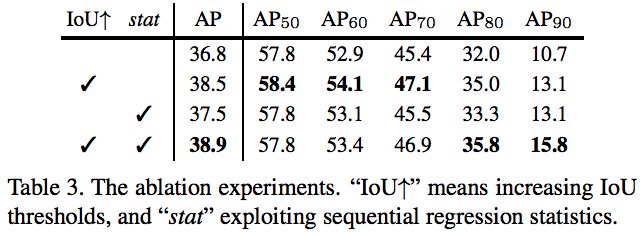
　　　　　 使用了iou，性能在提升；使用了stat性能也提升。同时使用iou和stat，总ap在上升，但是ap70以下的略微下降，ap80以上的提升，特别是ap90提升明显

　　　　　 延伸问题：为什么在用iou的基础上加stat，70以下反而下降？

对比实验4:

　　　　　 

　　　　　 联合预测的时候，1-2联合提升最明显；1-3比1-2也有提升，主要在高质量框上，整体ap提升了；但是再多回归一次，整体ap有略微下降，ap90以下的都下降了，

　　　　　 但是ap90上升了

　　　　　 延伸问题：为什么多一个stage，性能还下降了？

 

 cascade如何训练？

第一个stage选512个roi，训练之后把这些roi全给第二个stage的proposal_info_2nd(这个里面调用decodebbox层，也就是对当前的框进一步精修给下一个stage)，proposal_info_2nd中batchsize为-1，proposaltarget源码增加了batchsize为-1的情况，就是把所有的正负样本都考虑进来（实际上数量应该是小于512的），而不是原来默认的128.这个时候再跟gt进行assign，重新分配roi和gt给下一个stage.

 

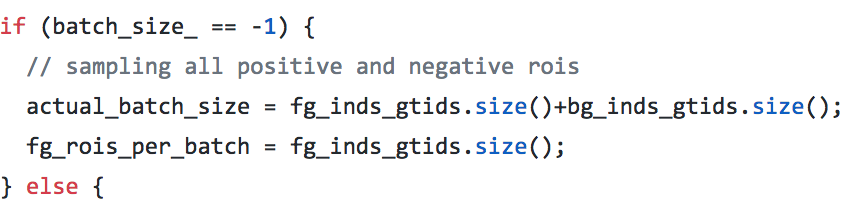
在decodebox层里面，还会把精修后错误的roi去掉，比如x1大于x2；同时，也会把和gt iou超过0.95的去掉，就是觉得这个已经够精确，不用再精修了

  // screen out mal-boxesif (this->phase_ == TRAIN) {for (int i = 0; i < num; i++) {const int base_index = i*bbox_dim+4;if (bbox_pred_data[base_index] > bbox_pred_data[base_index+2] || bbox_pred_data[base_index+1] > bbox_pred_data[base_index+3]) {valid_bbox_flags[i] = false;}}} // screen out high IoU boxes, to remove redundant gt boxesif (bottom.size()==3 && this->phase_ == TRAIN) {const Dtype* match_gt_boxes = bottom[2]->cpu_data();const int gt_dim = bottom[2]->channels();const float gt_iou_thr = this->layer_param_.decode_bbox_param().gt_iou_thr();for (int i = 0; i < num; i++) {const float overlap = match_gt_boxes[i*gt_dim+gt_dim-1];if (overlap >= gt_iou_thr) {valid_bbox_flags[i] = false;}}}

cascade如何测试 ？

bouding box regression是直接从最后一个stage得到的结果，即bbox_pre_3rd。

 

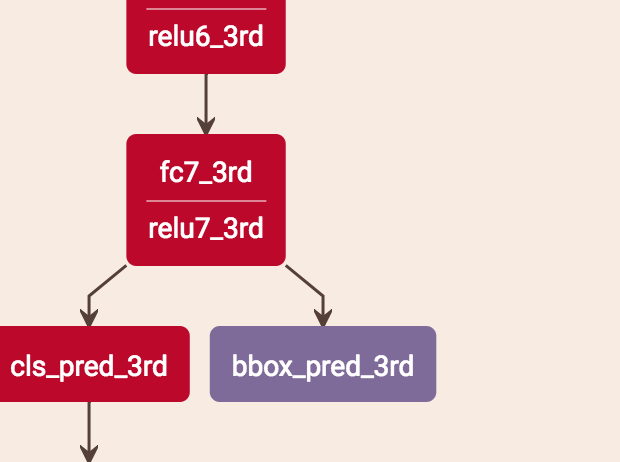
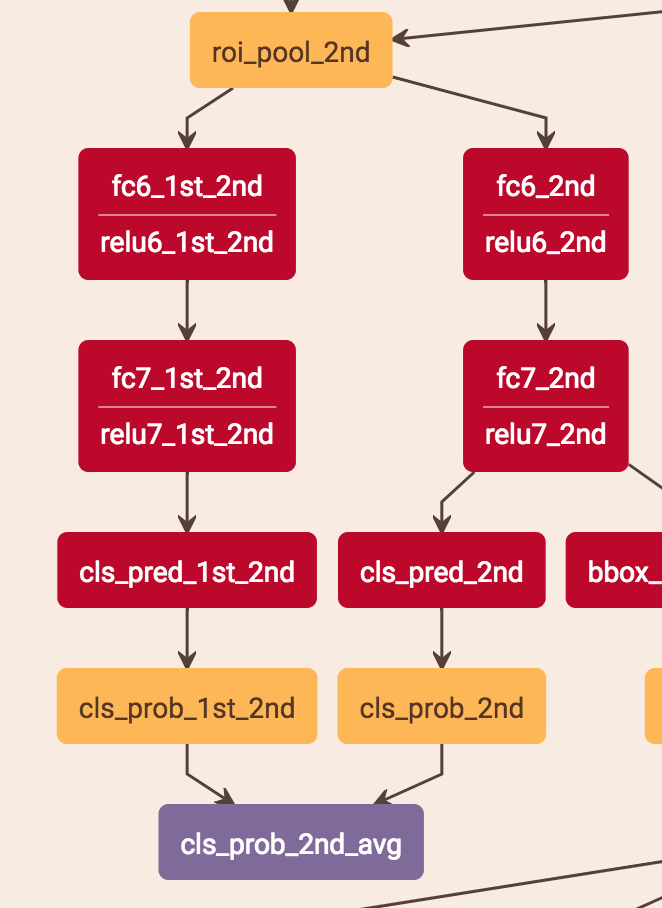
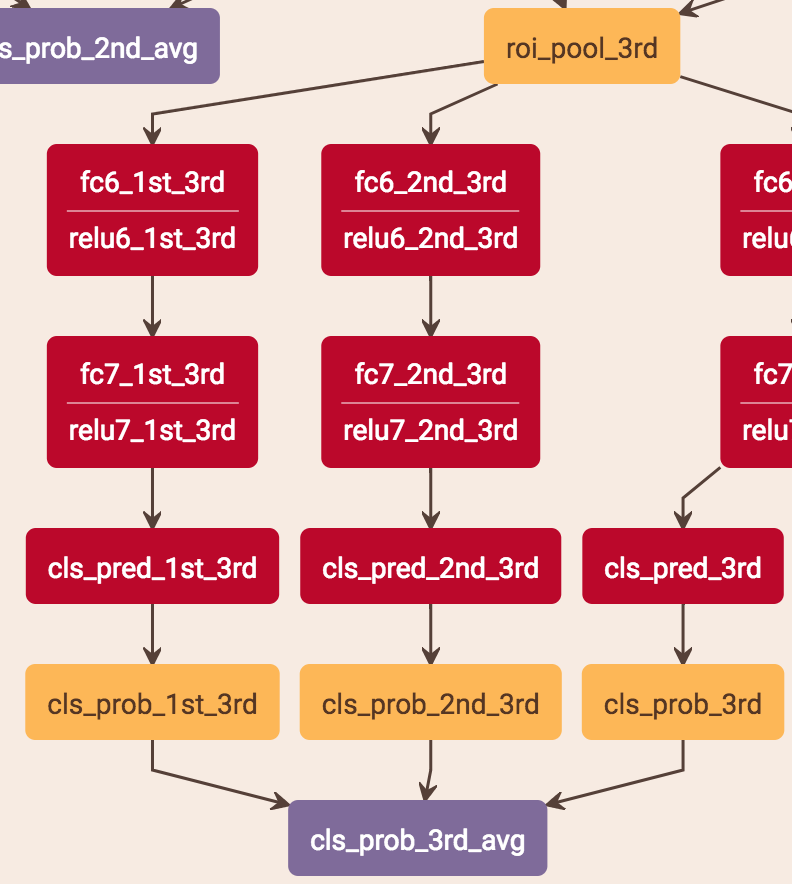
score的预测是把当前stage的score和之前层的score平均。stage2是把stage1的score*0.5 + stage2的score*0.5，stage3是把stage1的score*0.333 + stage2的score*0.333 + stage3的score*0.333。具体做法是：比如stage2的预测，roi-pooling出来的特征分别用两个分支得到两个score，这两个分支就是两层fc，一个用stage1的fc的参数，一个用stage2的fc的参数，这样就分别得到了两个stage的score再求平均。

注意：test.prototxt里面有cls_prob、cls_prob_2nd_avg、cls_prob_3rd_avg 3个输出，cls_prob是1的结果，cls_prob_2nd_avg是1+2的结果，cls_prob_3rd_avg是1+2+3的结果，他这3个输出应该是为了考虑最终的实验比较，最终的实际输出应该还是cls_prob_3rd_avg。

总的来说，cls是3个stage求平均，bouding box regression是直接从stage3获得

 

 为什么从3个stage到4个stage，性能还下降了？

可能是overfitting造成的：1.如果以faster来说的话，每个stage会增加两个大的fc和两个小的fc，这个参数量很大；  2.cascade代码中，每次回归之前，会把前一个stage的roi与gt的iou大于0.9的消除掉，stage越往高走，roi的个数是越会下降的。   3.并且也会把一些负样本去掉，因为cascade中每个stage会把roi不正常的框去掉，回归可能导致负样本这样

还有一点，就是可能模型本身做regression，多次regression后，好多框其实已经修正的比较好了，再去修正可能就是扰动，不能让性能很好提升，甚至有可能反而下降。

主要是往后特征没办法更好了吧，加更多也没有收益，只要Inference设计好，下降倒不太会

Cascade rcnn 3 4 也没下降，只是轻微影响一点，是饱和了