要求:从键盘上输入一元二次方程的三个参数,编程判断并求一元二次方程的实根(a,b,c均为整数)
算法分析:
一元二次方程是只含有一个未知数,且未知数的最高次数是二次的多项式方程。
一元二次方程经过整理都可化成一般形式ax²+bx+c=0(a≠0),其中ax²叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项。

(1)一元二次方程的解(根)的意义:能使一元二次方程左右两边相等的未知数的值称为一元二次方程的解。一般情况下,一元二次方程的解也称为一元二次方程的根(只含有一个未知数的方程的解也叫做这个方程的根)
(2)由代数基本定理,一元二次方程有且仅有两个根(重根按重数计算),根的情况由判别式(△=b²-4ac)决定。
判别式
利用一元二次方程根的判别式(△=b²-4ac)可以判断方程的根的情况。一元二次方程的根与根的判别式有如下关系:
①当 △>0 时,方程有两个不相等的实数根;
②当 △=0 时,方程有两个相等的实数根;
③当 △<0 时,方程无实数根,但有2个共轭复根。
代码实现:
#include
#include
#include
main()
{
int a,b,c,dt;
printf("请输入方程的三个参数a,b,c的值:\n");
scanf("%d %d %d",&a,&b,&c);
dt=b*b-4*a*c;
if(dt>0)
printf("X1=%f X2=%f\n",(-b+sqrt(dt))/(2*a)),(-b-sqrt(dt)/(2*a));
else if(dt=0)
printf("X1=X2=%f\n",(float)-b/(2*a));
else
printf("方程无实数根!\n");
getch();
}
程序运行测试:
(1)△<0 方程无实数根
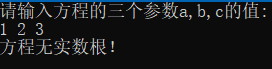
(2)△>0方程有两个不相等的实数根
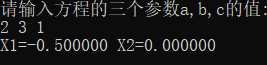
(3)△=0 方程有两个相等的实数根
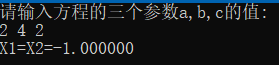

 关联与物理世界)










)



)
![BZOJ3670: [Noi2014]动物园](http://pic.xiahunao.cn/BZOJ3670: [Noi2014]动物园)

