
首先对Probabilistic Matrix Factorization这篇论文的核心公式进行讲解和推导;然后用Python代码在Movielens数据集上进行测试实验。
一、 背景知识
文中作者提到,传统的协同过滤算法有两个不足:
1).不能很好地处理规模非常大的数据;
2). 不能很好地处理那些只给出极少评分的用户。
概率矩阵分解则能很好的解决上述提到的这两个问题。
二、算法推导
2.1 定义和描述
假设有
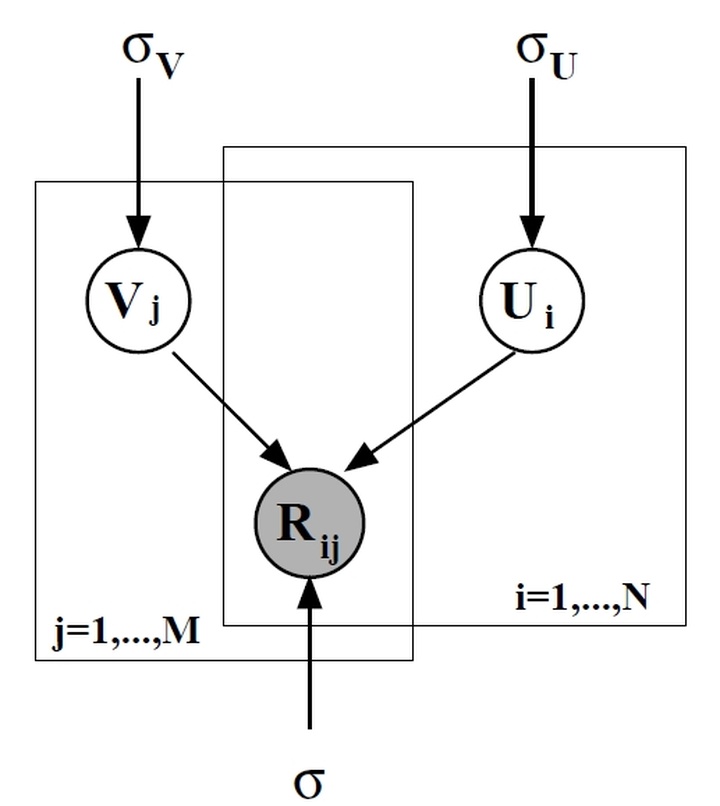
假设关于已知评分数据的条件分布满足高斯分布:
其中,
再假设用户潜在特征向量和商品潜在特征向量都服从均值为0的高斯先验分布,即:
注意公式(2)中的
然后,计算
等式两边取对数
2.2 关键处推导
此处插入取对数收到得到公式(3)的详细推导过程(对其中
其中
2.3 最优化目标函数
求等式(3)的最大值,等价于最小化目标函数:
其中,
等式
然后用随机梯度下降法(SGD)更新
其中
令
直到满足收敛条件或迭代至最大的迭代次数。
2.4 改进和优化
论文中还提到,用
原始评分
三、程序实现
3.1 代码及实现
伪代码如下所示:
Input: the number of latent factor K, the learning rata eta,
regularization parameters lambda_1,lambda_2, the max iteration Step,
and the rating matrix RInitialization: Initialize a random matrix for user matrix U and item matrix Vfor t = 1, 2,...Step dofor (u,i,r) in Rmake prediction pr=Ui^T*Vjerror e=r-prupdate Ui and Vj by (5) and (6)the algorithm suffers a loss (Ui, Vj, r)end for
end for下面用python,在 MovieLens 100K 这个数据集上实现PMF算法。
核心代码如下所示:
def update(p, q, r, learning_rate=0.001, lamda_regularizer=0.1):error = r - np.dot(p, q.T) p = p + learning_rate*(error*q - lamda_regularizer*p)q = q + learning_rate*(error*p - lamda_regularizer*q)loss = 0.5 * (error**2 + lamda_regularizer*(np.square(p).sum() + np.square(q).sum()))return p,q,loss3.2 实验结果
当训练集:测试集=8:2时,可得到最终的RMSE为0.92左右,实验曲线如下所示:
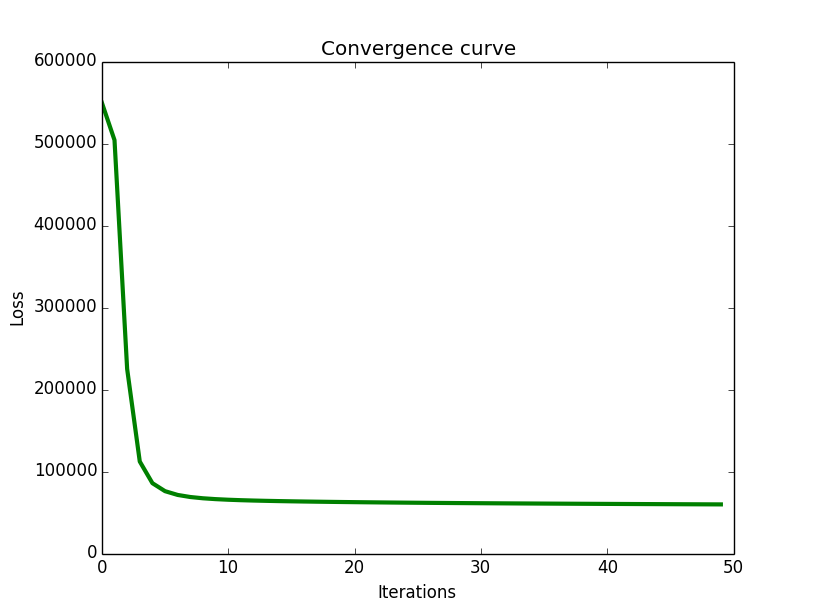
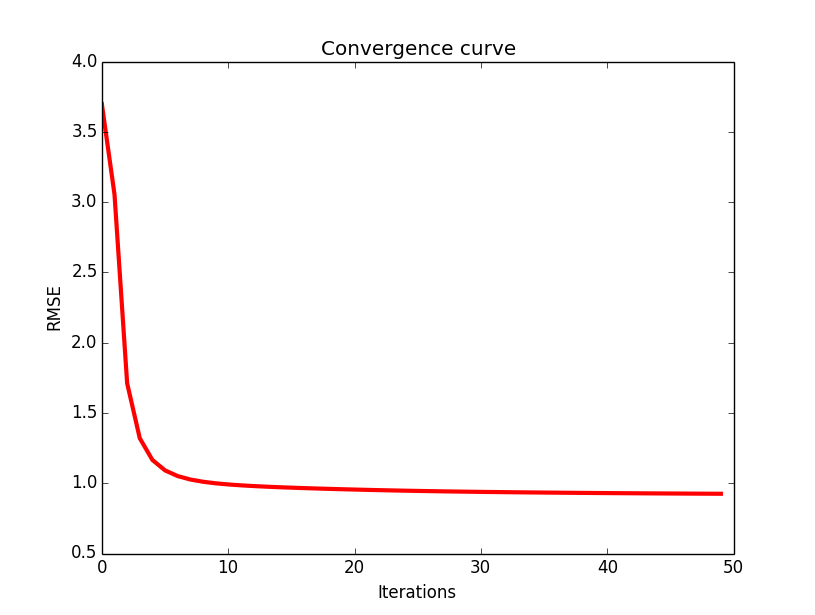
完整项目下载地址:
https://github.com/XiuzeZhou/Recommender-Systemsgithub.com更多 矩阵分解内容和程序,请看我的最新博文:
周秀泽:推荐系统系列之二:矩阵分解家族zhuanlan.zhihu.com
参考资料:
[1] 小木,推荐系统之概率矩阵分解的详细推导过程(Probabilistic Matrix Factorization,PMF)
[2] 追溯星霜,PMF:概率矩阵分解

)











)





