HDU 2243 考研路茫茫——单词情结求长度小于等于L的通路总数的方法

http://acm.hdu.edu.cn/showproblem.php?pid=2243

这是一题AC自动机 + 矩阵快速幂的题目，

首先知道总答案应该是26^1 + 26^2 + 26^3 .... + 26^L，用等比数列的前n项和是无法做的，因为出现小数。

这个可以直接看到F[n] = 26 * F[n - 1] + 26，然后矩阵快速幂即可。

然后需要减去那些一个词根都不包含的单词的总数，这个可以用AC自动机算出来。就是至少包含一个词根的答案。

现在关键就是求，长度小于等于L的通路总数。

我们知道通路等于L的通路总数，正是一个可达矩阵e[i][j]的L次幂。

那么小于等于L的，也就是e + e^2 + e^3 + e^4 + ... + e^L

这是无法求的。

做法是新增一个节点，然后每一个节点都和这个新的节点连上一条边。

假设本来的可达矩阵是

e[1][1] = 1, e[1][2] = 1, e[1][3] = 1

e[2][1] = 0, e[2][2] = 0, e[2][3] = 1;

e[3][1] = 0, e[3][2] = 0, e[3][3] = 0;

那么长度是2的通路数就是，e^2，然后得到了这个图。

所以长度是2的通路数，是4。e[1][1] ---> e[1][1]，e[1][1]--->e[1][2]。e[1][1] ---> e[1][3]，e[1][2]--->e[2][3]

那么长度是1的通路数就不能统计了，就是e[1][1]、e[1][2]、e[1][3]丢失了。

那么我们新增一个节点，使得其他本来的节点都和它连一条边。

然后算e^2的时候，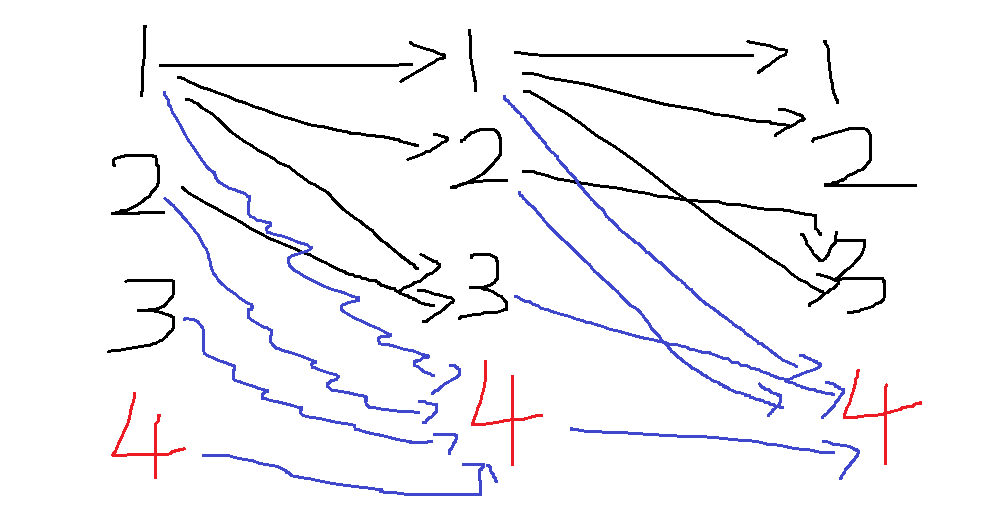

就会把e[1][1]记录到e[1][1]-->e[1][4]中，所以记录成功。、

然后e[1][4]本来是不存在的，所以这条路径是多余的，

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <assert.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;#include <iostream>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <bitset>
typedef unsigned long long int ULL;
const int N = 26;
struct node {int flag;int id;struct node *Fail;    //失败指针，匹配失败，跳去最大前后缀struct node *pNext[N];
} tree[100 * 20];
int t;     //字典树的节点
struct node *create() {   //其实也只是清空数据而已，多case有用struct node *p = &tree[t++];p->flag = 0;p->Fail = NULL;p->id = t - 1;for (int i = 0; i < N; i++) {p->pNext[i] = NULL;}return p;
}
void toinsert(struct node **T, char str[]) {struct node *p = *T;if (p == NULL) {p = *T = create();}for (int i = 1; str[i]; i++) {int id = str[i] - 'a';if (p->pNext[id] == NULL) {p->pNext[id] = create();}p = p->pNext[id];}p->flag++;    //相同的单词算两次return ;
}
void BuiltFail(struct node **T) {//根节点没有失败指针,所以都是需要特判的//思路就是去到爸爸的失败指针那里，找东西匹配，这样是最优的struct node *p = *T; //用个p去代替修改struct node *root = *T;if (p == NULL) return ;//树上bfs,要更改的是p->pNext[i]->Failstruct node *que[t + 20]; //这里的t是节点总数，字典树那里统计的，要用G++编译int head = 0, tail = 0;que[tail++] = root;while (head < tail) {p = que[head]; //p取出第一个元素 ★for (int i = 0; i < N; i++) { //看看存不存在这个节点if (p->pNext[i] != NULL) { //存在的才需要管失败指针。if (p == root) { //如果爸爸是根节点的话p->pNext[i]->Fail = root; //指向根节点} else {struct node *FailNode = p->Fail; //首先找到爸爸的失败指针while (FailNode != NULL) {if (FailNode->pNext[i] != NULL) { //存在p->pNext[i]->Fail = FailNode->pNext[i];if (FailNode->pNext[i]->flag) {p->pNext[i]->flag = 1;}break;}FailNode = FailNode->Fail; //回溯
                    }if (FailNode == NULL) { //如果还是空，那么就指向根算了p->pNext[i]->Fail = root;}}que[tail++] = p->pNext[i]; //这个id是存在的，入队bfs} else if (p == root) {  //变化问题，使得不存在的边也建立起来。p->pNext[i] = root;} else {p->pNext[i] = p->Fail->pNext[i]; //变化到LCP。可以快速匹配到病毒。
            }}head++;}return ;
}const int maxn = 30 + 3;
struct Matrix {ULL a[maxn][maxn];int row;int col;
};
//应对稀疏矩阵，更快。
struct Matrix matrix_mul(struct Matrix a, struct Matrix b) { //求解矩阵a*b%MODstruct Matrix c = {0};  //这个要多次用到，栈分配问题，maxn不能开太大，//LL的时候更加是，空间是maxn*maxn的，这样时间用得很多，4和5相差300msc.row = a.row; //行等于第一个矩阵的行c.col = b.col; //列等于第二个矩阵的列for (int i = 1; i <= a.row; ++i) {for (int k = 1; k <= a.col; ++k) {if (a.a[i][k]) { //应付稀疏矩阵，0就不用枚举下面了for (int j = 1; j <= b.col; ++j) {c.a[i][j] += a.a[i][k] * b.a[k][j];}}}}return c;
}
struct Matrix quick_matrix_pow(struct Matrix ans, struct Matrix base, int n) {
//求解a*b^n%MODwhile (n) {if (n & 1) {ans = matrix_mul(ans, base);//传数组不能乱传,不满足交换律
        }n >>= 1;base = matrix_mul(base, base);}return ans;
}int n, L;
char str[222];
void work() {t = 1;struct node *T = NULL;for (int i = 1; i <= n; ++i) {scanf("%s", str + 1);toinsert(&T, str);}BuiltFail(&T);t--;Matrix e = {0};e.row = e.col = t + 1;for (int i = 1; i <= t; ++i) {if (tree[i].flag) continue;int id1 = tree[i].id;for (int j = 0; j < N; ++j) {if (tree[i].pNext[j]->flag) continue;int id2 = tree[i].pNext[j]->id;e.a[id1][id2]++;}}t++;for (int i = 1; i <= t; ++i) {e.a[i][t] = 1;}Matrix I = {0};I.row = I.col = t;for (int i = 1; i <= t; ++i) {I.a[i][i] = 1;}Matrix res = quick_matrix_pow(I, e, L);I.row = 1, I.col = 2;I.a[1][1] = 0, I.a[1][2] = 1;e.row = e.col = 2;e.a[1][1] = 26, e.a[1][2] = 0;e.a[2][1] = 26, e.a[2][2] = 1;Matrix res2 = quick_matrix_pow(I, e, L);ULL ans = res2.a[1][1];
//    cout << ans << endl;for (int i = 1; i <= t; ++i) {ans -= res.a[1][i];}ans++; //减了一个多余的路径cout << ans << endl;
}int main() {
#ifdef localfreopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endifwhile (scanf("%d%d", &n, &L) > 0) work();return 0;
}