CF Round410 D. Mike and distribution

D. Mike and distribution 构造法

798D - Mike and distribution

In the beginning, it's quite easy to notice that the condition " 2·(ap1 + ... + apk) is greater than the sum of all elements in A " is equivalent to " ap1 + ... + apk is greater than the sum of the remaining elements in A ".

Now, let's store an array of indices C with Ci = i and then sort it in decreasing order according to array A, that is we must have ACi ≥ ACi + 1.

Our answer will always have size 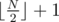. First suppose that N is odd. Add the first index to our set, that is make p1 = C1. Now, for the remaining elements, we will consider them consecutively in pairs. Suppose we are at the moment inspecting AC2k and AC2k + 1. If BC2k ≥ BC2k + 1 we make pk + 1 = C2k, else we make pk + 1 = C2k + 1.

Why does this subset work? Well, it satisfies the condition for B because each time for consecutive non-intersecting pairs of elements we select the bigger one, and we also add BC1 to the set, so in the end the sum of the selected elements will be bigger than the sum of the remaining ones.

It also satisfies the condition for A, because Ap1 is equal or greater than the complement element of p2 (that is — the index which we could've selected instead of p2 from the above procedure — if we selected C2k then it would be C2k + 1 and vice-versa). Similarly Ap2 is greater than the complement of p3 and so on. In the end we also add the last element from the last pair and this makes the sum of the chosen subset strictly bigger than the sum of the remaining elements.

The case when N is even can be done exactly the same as when N is odd, we just pick the last remaining index in the end.

The complexity is .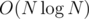

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 7;
int a[N], b[N], c[N], p[N/2];
bool cmp(int i, int j) {return a[i] > a[j];
}
int main()
{//ios::sync_with_stdio(0);int n;while(~scanf("%d", &n)) {for (int i = 1; i <= n; ++i) {scanf("%d", a +i);c[i] = i;}for (int i = 1; i <= n; ++i)scanf("%d", b + i);sort(c + 1, c + 1 + n, cmp);int k = n + 1 >> 1, cur = 0;p[++cur] = c[1];b[n + 1] = 0;//最边界小值 for (int i = 2; i <= n; i += 2)  //cur = k ?p[++cur] = b[c[i]] > b[c[i + 1]] ? c[i] : c[i+1];printf("%d\n%d", cur, p[1]); for (int i = 2; i <= cur; ++i)printf(" %d", p[i]);puts("");}return 0;
}