贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率和边缘概率的一则定理。
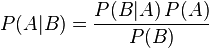
在参数估计中可以写成下面这样：
这个公式也称为逆概率公式，可以将后验概率转化为基于似然函数和先验概率的计算表达式，即
在贝叶斯定理中，每个名词都有约定俗成的名称：
P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
P(A|B)是已知B发生后A的条件概率(在B发生的情况下A发生的可能性)，也由于得自B的取值而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
P(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）.
按这些术语，Bayes定理可表述为：
后验概率 = (相似度*先验概率)/标准化常量，也就是说，后验概率与先验概率和相似度的乘积成正比。
另外，比例P(B|A)/P(B)也有时被称作标准相似度（standardised likelihood），Bayes定理可表述为：
后验概率 = 标准相似度*先验概率
贝叶斯估计
贝叶斯估计是在MAP上做进一步拓展，此时不直接估计参数的值，而是允许参数服从一定概率分布。极大似然估计和极大后验概率估计，都求出了参数theta的值，而贝叶斯推断则不是，贝叶斯推断扩展了极大后验概率估计MAP（一个是等于，一个是约等于）方法，它根据参数的先验分布P(theta)和一系列观察X，求出参数theta的后验分布P(theta|X)，然后求出theta的期望值，作为其最终值。另外还定义了参数的一个方差量，来评估参数估计的准确程度或者置信度。
贝叶斯公式
现在不是要求后验概率最大，这样就需要求,即观察到的evidence的概率，由全概率公式展开可得
当新的数据被观察到时，后验概率可以自动随之调整。但是通常这个全概率的求法是贝叶斯估计比较有技巧性的地方。
用贝叶斯估计来做预测
如果我们想求一个新值的概率，可以由下面公式来计算。
此时第二项因子在上的积分不再等于1，这就是和MLE及MAP很大的不同点。
