排序算法[转]

笔者最近学习算法，学了很久也只弄懂了几个排序算法，在这里晒一下下，作为以后参考之用。

一、为什么要研究排序问题

许多计算机科学家认为，排序算法是算法学习中最基本的问题，原因有以下几点：

l  有时候应用程序本身需要对信息进行排序，如为了准备客户账目，银行需要对支票账号进行排序

l  很多算法将排序作为关键子程序

l  现在已经有很多排序算法，它们采用各种技术

l  排序时一个可以证明其非平凡下界的问题，并可以利用排序问题的下界证明其他问题的下界

l  在实现排序算法是很多工程问题即浮出水面

二、排序问题的形式化定义

输入：由n个数组成的一个序列<a₁,a₂,……,a_n>

输出：对输入序列的一个排列（重排）<a₁’,a₂’,……,a_n’>,使得a₁’ ≤a₂’ ≤……≤a_n’

【说明】在实际中，待排序的数很少是孤立的值，它们通常是成为激励的数据集的一个部分，每个记录有一个关键字key,是待排序的值，其他数据位卫星数据，它们通常以key为中心传递。

三、相关概念

1.         排序的稳定性：在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生变化，则称这种排序方法是不稳定的。

A.       稳定排序：插入排序、冒泡排序、鸡尾酒排序、计数排序、合并交换排序、归并排序、基数排序、桶排序、鸽巢排序

B.        不稳定排序：选择排序、堆排序、希尔排序、快速排序

2.         内部、外部排序：在排序过程中，若整个文件都是放在内存中处理，排序时不涉及数据的内、外存交换，则称之为内部排序(简称内排序)；反之，若排序过程中要进行数据的内、外存交换，则称之为外部排序。

3.     待排文件的常用存储方式：

A.     顺序表：对记录本身进行物理重排（即通过关键字之间的比较判定，将记录移到合适的位置

B.     链表：无须移动记录，仅需修改指针

C.     用顺序的方式存储待排序的记录，但同时建立一个辅助表：对辅助表的表目进行物理重排（即只移动辅助表的表目，而不移动记录本身）。

4.     影响排序效果的因素

A.     待排序的记录数目n

B.     记录的大小(规模)

C.     关键字的结构及其初始状态

D.    对稳定性的要求

E.     语言工具的条件

F.     存储结构

G.    时间和辅助空间复杂度等

四、排序算法的分类（内部排序）

1.         比较类排序：排序结果中各元素的次序基于输入元素间的比较

A.       比较排序算法的下界

比较排序可以被抽象为决策树。一棵决策树是一棵满二叉树，表示某排序算法作用于给定输入所做的所有比较，而忽略控制结构和数据移动。

在决策树中，对每个节点都注明i，j（1≤i，j≤n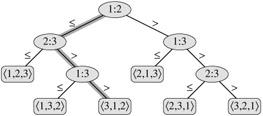），对每个叶节点都注明排列<π(1), π(2),……, π(n)>。排序算法的执行对应于遍历一条从根到叶节点的路径。在每个内节点作比较a_i≤a_j，其左子树决定a_i≤a_j之后的比较，其右子树决定a_i＞a_j之后的比较。当到达一个叶节点时排序算法就已经确定了顺序。要使排序算法能正确的工作，其必要条件是n个元素的n!种排列都要作为决策树的一个叶节点出现。在决策树中，从根到任意一个可达叶节点之间最长路径的长度（决策树的高度）表示对应的排序算法中最坏情况下的比较次数。对于一棵高度为h，具有l个可达叶节点的决策树有n! ≤l≤2^h，则有h≥lg(n!)=Ω(nlgn)

B.        常见的比较类排序

a)         选择类排序：选择排序、堆排序

b)        插入类排序：插入排序、二叉插入、两路插入、希尔排序

c)         交换类排序：冒泡排序、鸡尾酒排序、合并交换排序、快速排序

d)        归并排序

2.         非比较类排序：计数排序、基数排序、桶排序、鸽巢排序

五、常用的排序算法 

1.         比较类排序

A.       选择类排序

a)         选择排序（Selection Sort）——原地排序、不稳定排序

【思路】首先找出A中最小元素，并将其与A[0]中元素交换；接着找出A中次最小元素，并将其与A[1]中元素交换；对A中头n-1个元素继续这一过程

【代码】

        #region 选择排序

/// <summary>
/// 选择排序
/// 最差时间复杂度 Θ(n²) 
/// 最优时间复杂度 Θ(n²) 
/// 平均时间复杂度 Θ(n²) 
/// 原地排序
/// 【排序过程】
/// 1、首先在未排序序列中找到最小元素，存放到排序序列的起始位置
/// 2、然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾
/// 3、以此类推，直到所有元素均排序完毕。
/// </summary>
/// <param name="Array">待排序的数组</param>
        public static void SelectionSort(int[] Array)
        {
for (int i = 0; i < Array.Length; i++)
            {
for (int j = i + 1; j < Array.Length; j++)
                {
if (Array[j] < Array[i])
                    {
                        Swap(ref Array[i], ref Array[j]);//交换数据
                    }
                }
            }
        }

#endregion

　　

【时间复杂度分析】选择排序的比较操作为n(n − 1) / 2次，交换操作介于0和n(n − 1) / 2次之间，故其时间复杂度为Θ(n²)

b)         堆排序（Heap Sort）

 六、代码

【二叉堆】（二叉）堆数据结构是一种数组对象，可以被视为一棵完全二叉树。二叉堆有两种：大顶堆和小顶堆（最大堆和最小堆）。大顶堆中每个节点的值不大于其父节点的值，这样，堆中最大的元素就存放在根节点中。

 

 

【思路】首先将输入数组构造成大顶堆；由于数组中最大元素为A[0]，将其与A[n]交换使其达到最终正确位置；在堆中除去A[n]，并将A[1…n]保持为大顶堆；重复上述过程，直到堆大小降为2。

【代码】由思路知堆排序中应包含构造大顶堆和保持大顶堆子程序。MaxHeapify方法被用来保持大顶堆，其时间复杂度为O(lgn)

        /// <summary>
/// 调整数组,保持大顶堆性质
/// </summary>
/// <param name="Array">待保持大顶堆的数组</param>
/// <param name="i">大顶堆的根</param>
/// <param name="HeapSize">堆的大小</param>
        private static void MaxHeapify(int[] Array, int i, int HeapSize)
        {
int left = i * 2;
int right = left + 1;
int largest;
if (left < HeapSize && Array[left] > Array[right])
            {
                largest = left;
            }
else
            {
                largest = i;
            }
if (right < HeapSize && Array[right] > Array[largest])
            {
                largest = right;
            }
if (largest != i)
            {
                Swap(ref Array[i], ref Array[largest]);
                MaxHeapify(Array, largest, HeapSize);
            }
        }

/// <summary>
/// 调整数组,保持大顶堆性质(迭代实现)
/// </summary>
/// <param name="Array">待保持大顶堆的数组</param>
/// <param name="i">大顶堆的根</param>
/// <param name="HeapSize">堆的大小</param>
        private static void MaxHeapifyWithoutRecursive(int[] Array, int i, int HeapSize)
        {
while (i <= HeapSize)
            {
int left = i * 2;
int right = left + 1;
int largest;
if (left < HeapSize && Array[left] > Array[right])
                {
                    largest = left;
                }
else
                {
                    largest = i;
                }
if (right < HeapSize && Array[right] > Array[largest])
                {
                    largest = right;
                }
if (largest != i)
                {
                    Swap(ref Array[i], ref Array[largest]);
                    i = largest;
                }
else
                {
return;
                }
            }
        }

　　

        /// <summary>
/// 构造大顶堆
/// </summary>
/// <param name="Array">待构造大顶堆的数组</param>
        private static void BuildMaxHeapify(int[] Array)
        {
int HeapSize = Array.Length;
for (int i = (Array.Length - 1) / 2; i >= 0; i--)
            {
// MaxHeapify(Array, i, HeapSize);              //递归实现
                MaxHeapifyWithoutRecursive(Array, i, HeapSize); //迭代实现
            }
        }

　　

堆排序代码如下： 

 【时间复杂度分析】调用BuildMaxHeap时间为O(n)，n-1次调用MaxHeapify，每次时间为O(lgn)，故堆排序时间复杂度为O(nlgn)   

using System;namespace Algorithms
{public class Sort{static Random random = new Random();#region 交换数据/// <summary>/// 交换数据/// </summary>/// <param name="a">待交换值a</param>/// <param name="b">待交换值b</param>/// <returns>是否成功</returns>public static bool Swap(ref int a, ref int b){if (!Equals(a, b)){a ^= b;b ^= a;a ^= b;return true;}else{return false;}}#endregion#region 交换类排序#region 冒泡排序/// <summary>/// 冒泡排序（Bubble Sort）/// </summary>/// 最坏时间复杂度 O(n²)/// 最优时间复杂度 O(n)/// 平均时间复杂度 O(n²)/// 原地排序/// 不稳定排序/// 【排序过程】/// 1、比较相邻的元素。如果第一个比第二个大，就交换他们两个。/// 2、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。 /// 3、针对所有的元素重复以上的步骤，除了最后一个。 /// 4、持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。 /// <param name="Array">待排序的数组</param>public static void BubbleSort(int[] Array){for (int i = 0; i < Array.Length; i++){for (int j = Array.Length - 1; j > i; --j){if (Array[j] < Array[j - 1]){Swap(ref Array[j], ref Array[j - 1]);}}}}#endregion#region 快速排序/// <summary>/// 快速排序划分/// </summary>/// <param name="Array">待分划的数组</param>/// <param name="p">待分划数组下界</param>/// <param name="r">待分划数组上界</param>/// <returns>分划元素位置</returns>private static int Partition(int[] Array, int p, int r){int x = Array[r];int i = p - 1;for (int j = p; j < r; j++){if (Array[j] <= x){++i;Swap(ref  Array[i], ref Array[j]);}}Swap(ref Array[i + 1], ref Array[r]);return i + 1;}/// <summary>/// 快速排序/// </summary>/// 最差时间复杂度 Θ(n²) /// 最优时间复杂度 Θ(nlogn) /// 平均时间复杂度 Θ(nlogn) /// 原地排序/// 非稳定排序/// 【排序过程】/// 1、从数列中挑出一个元素，称为 "基准"， /// 2、分割：重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分割之后，该基准是它的最后位置。 /// 3、递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。 /// <param name="Array">待排序的数组</param>/// <param name="p">待排序数组下界</param>/// <param name="r">待排序数组上界</param>public static void QuickSort(int[] Array, int p, int r){if (p < r){int q = Partition(Array, p, r);QuickSort(Array, p, q - 1);QuickSort(Array, q, r);}}/// <summary>/// 快速排序划分(随机化)/// </summary>/// <param name="Array">待分划的数组</param>/// <param name="p">待分划数组下界</param>/// <param name="r">待分划数组上界</param>/// <returns>分划元素位置</returns>private static int RandomizedPartition(int[] Array, int p, int r){int i = random.Next(p, r + 1);Swap(ref Array[r], ref Array[i]);return Partition(Array, p, r);}/// <summary>/// 快速排序(随机化)/// </summary>/// <param name="Array">待排序的数组</param>/// <param name="p">待排序数组下界</param>/// <param name="r">待排序数组上界</param>public static void RandomizedQuickSort(int[] Array, int p, int r){if (p < r){int q = RandomizedPartition(Array, p, r);RandomizedQuickSort(Array, p, q - 1);RandomizedQuickSort(Array, q, r);}}/// <summary>/// Hoare划分/// </summary>/// <param name="Array">待分划的数组</param>/// <param name="p">待分划数组下界</param>/// <param name="r">待分划数组上界</param>/// <returns>分划元素位置</returns>private static int HoarePartition(int[] Array, int p, int r){int x = Array[p];int i = p - 1;int j = r + 1;while (true){do{--j;} while (Array[j] <= x);do{++i;} while (Array[i] >= x);if (i < j){int t = Array[i];Array[i] = Array[j];Array[j] = t;}else{return j;}}}#endregion#endregion#region 选择类排序#region 选择排序/// <summary>/// 选择排序/// 最差时间复杂度 О(n²) /// 最优时间复杂度 О(n²) /// 平均时间复杂度 О(n²) /// 原地排序/// 【排序过程】/// 1、首先在未排序序列中找到最小元素，存放到排序序列的起始位置/// 2、然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾/// 3、以此类推，直到所有元素均排序完毕。/// </summary>/// <param name="Array">待排序的数组</param>public static void SelectionSort(int[] Array){for (int i = 0; i < Array.Length; i++){for (int j = i + 1; j < Array.Length; j++){if (Array[j] < Array[i]){Swap(ref Array[i], ref Array[j]);}}}}#endregion#region 堆排序/// <summary>/// 调整数组,保持大顶堆性质/// </summary>/// <param name="Array">待保持大顶堆的数组</param>/// <param name="i">大顶堆的根</param>/// <param name="HeapSize">堆的大小</param>private static void MaxHeapify(int[] Array, int i, int HeapSize){int left = i * 2;int right = left + 1;int largest;if (left < HeapSize && Array[left] > Array[right]){largest = left;}else{largest = i;}if (right < HeapSize && Array[right] > Array[largest]){largest = right;}if (largest != i){Swap(ref Array[i], ref Array[largest]);MaxHeapify(Array, largest, HeapSize);}}/// <summary>/// 调整数组,保持大顶堆性质(迭代实现)/// </summary>/// <param name="Array">待保持大顶堆的数组</param>/// <param name="i">大顶堆的根</param>/// <param name="HeapSize">堆的大小</param>private static void MaxHeapifyWithoutRecursive(int[] Array, int i, int HeapSize){while (i <= HeapSize){int left = i * 2;int right = left + 1;int largest;if (left < HeapSize && Array[left] > Array[right]){largest = left;}else{largest = i;}if (right < HeapSize && Array[right] > Array[largest]){largest = right;}if (largest != i){Swap(ref Array[i], ref Array[largest]);i = largest;}else{return;}}}/// <summary>/// 构造大顶堆/// </summary>/// <param name="Array">待构造大顶堆的数组</param>private static void BuildMaxHeapify(int[] Array){int HeapSize = Array.Length;for (int i = (Array.Length - 1) / 2; i >= 0; i--){// MaxHeapify(Array, i, HeapSize);MaxHeapifyWithoutRecursive(Array, i, HeapSize);}}/// <summary>/// 堆排序/// 最差时间复杂度 O(nlogn) /// 最优时间复杂度 O(nlogn)/// 平均时间复杂度 Θ(nlogn)/// 原地排序/// 不稳定排序/// 【排序过程】/// 1、建立一个大顶堆/// 2、把堆首（最大值）和堆尾互换 /// 3、把堆的尺寸缩小1，并保持大顶堆/// 4、重复2号步骤，直到堆的尺寸为1 /// </summary>/// <param name="Array">待排序的数组</param>public static void HeapSort(int[] Array){int HeapSize = Array.Length;BuildMaxHeapify(Array);for (int i = Array.Length - 1; i > 0; i--){int t;t = Array[0];Array[0] = Array[i];Array[i] = t;MaxHeapifyWithoutRecursive(Array, 0, --HeapSize);//MaxHeapify(Array, 0, --HeapSize);}}#endregion#endregion#region 插入类排序#region 插入排序/// <summary>/// 插入排序(非递归算法)/// 平均时间复杂度 Θ(n²) /// 原地排序/// 稳定排序/// 【排序过程】/// 1、从第一个元素开始，该元素可以认为已经被排序 /// 2、取出下一个元素，在已经排序的元素序列中从后向前扫描 /// 3、如果该元素（已排序）大于新元素，将该元素移到下一位置 /// 4、重复步骤3，直到找到已排序的元素小于或者等于新元素的位置 /// 5、将新元素插入到该位置中 /// 6、重复步骤2 /// </summary>/// <param name="Array">待排序的数组</param>public static void InsertionSort(int[] Array){for (int j = 1; j < Array.Length; j++){int key = Array[j];int i = j - 1;while (i >= 0 && Array[i] > key){Array[i + 1] = Array[i];--i;}Array[i + 1] = key;}}/// <summary>/// 插入排序(递归算法)/// </summary>/// <param name="Array">待排序的数组</param>/// <param name="length">要排序的长度</param>public static void InsertionSort(int[] Array, int length){if (length == 0){return;}else{InsertionSort(Array, length - 1);}int key = Array[length];while (Array[length] >= key){Array[length + 1] = Array[length];--length;}Array[length] = key;}#endregion#region Shell排序/// <summary>/// Shell排序（递减增量排序）/// </summary>/// 【排序过程】/// 1、取一个小于n的整数d1作为第一个增量，把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。/// 2、先在各组内进行直接插入排序；/// 3、然后，取第二个增量d2＜d1重复上述的分组和排序，直至所取的增量dt=1(dt＜dt-1＜…＜d2＜d1)为止。/// <param name="Array">待排序的数组</param>public static void shellsort(int[] Array){int temp;int increment; //增量 int length = Array.Length;for (increment = length / 2; increment > 0; increment /= 2){for (int i = increment; i < length; ++i){int j;temp = Array[i];for (j = i; j >= increment; j -= increment){if (temp < Array[j - increment])Array[j] = Array[j - increment];elsebreak;}Array[j] = temp;}}}#endregion#endregion#region 归并类排序#region 归并排序/// <summary>/// 归并数组(使用哨兵)/// <para>归并数组Array[lower,mid]与Array[mid+1,upper]</para>/// </summary>/// <param name="Array">待归并的数组</param>/// <param name="lower">待归并数组下界</param>/// <param name="mid">待归并数组分界</param>/// <param name="upper">待归并数组上界</param>private static void MergeWithSentinel(int[] Array, int lower, int mid, int upper){int n1 = mid - lower + 1;int n2 = upper - mid;int[] L = new int[n1 + 1];int[] R = new int[n2 + 1];int i = 0;int j = 0;for (i = 0; i < n1; i++){L[i] = Array[lower + i];}for (i = 0; i < n2; i++){R[i] = Array[mid + i + 1];}L[n1] = R[n2] = int.MaxValue;i = 0;for (int k = lower; k < upper; k++){if (L[i] < R[j]){Array[k] = L[i++];}else{Array[k] = R[j++];}}}/// <summary>/// 归并数组(不使用哨兵)/// <para>归并数组Array[lower,mid]与Array[mid+1,upper]</para>/// </summary>/// <param name="Array">待归并的数组</param>/// <param name="lower">待归并数组下界</param>/// <param name="mid">待归并数组分界</param>/// <param name="upper">待归并数组上界</param>private static void Merge(int[] Array, int lower, int mid, int upper){int n1 = mid - lower + 1;int n2 = upper - mid;int[] L = new int[n1];int[] R = new int[n2];int i = 0;int j = 0;for (i = 0; i < n1; i++){L[i] = Array[lower + i];}for (i = 0; i < n2; i++){R[i] = Array[mid + i + 1];}i = 0;for (int k = lower; k < upper; k++){if (L[i] < R[j]){Array[k] = L[i++];}else{Array[k] = R[j++];}if (i == n1){while (j < n2){Array[++k] = R[j++];}}if (j == n2){while (i < n1){Array[++k] = L[i++];}}}}/// <summary>/// 归并排序/// </summary>/// 最差时间复杂度 Θ(nlogn) /// 最优时间复杂度 Θ(n) /// 平均时间复杂度 Θ(nlogn)/// 非原地排序/// 稳定排序/// 【排序过程】/// 1、申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列 /// 2、设定两个指针，最初位置分别为两个已经排序序列的起始位置 /// 3、比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置 /// 4、重复步骤3直到某一指针达到序列尾 /// 5、将另一序列剩下的所有元素直接复制到合并序列尾 /// <param name="Array">待排序的数组</param>/// <param name="lower">待排序数组下界</param>/// <param name="upper">待排序数组上界</param>public static void MergeSort(int[] Array, int lower, int upper){if (lower < upper){int mid = (lower + upper) / 2;MergeSort(Array, lower, mid);MergeSort(Array, mid + 1, upper);Merge(Array, lower, mid, upper);}}#endregion#endregion#region 非比较类排序#region 计数排序/// <summary>/// 获取数组最大数/// </summary>/// <param name="Array">要取最大数的数组</param>/// <returns>数组最大数</returns>private static int GetLargest(int[] Array){int largest = 0;foreach (var i in Array){if (largest < i){largest = i;}}return largest;}/// <summary>/// 计数排序/// </summary>/// <param name="Array">待排序的数组</param>public static void CountingSort(int[] Array){int largest = GetLargest(Array) + 1;int[] B = new int[Array.Length];int[] C = new int[largest];for (int i = 0; i < largest; i++){C[i] = 0;}for (int j = 0; j < Array.Length; j++){++C[Array[j]];}for (int i = 1; i < largest; i++){C[i] += C[i - 1];}for (int j = Array.Length - 1; j >= 0; --j){B[C[Array[j]] - 1] = Array[j];C[Array[j]] = C[Array[j]] - 1;}for (int i = 0; i < Array.Length; i++){Array[i] = B[i];}}#endregion#endregion}
}

原文链接：http://www.cnblogs.com/kingwolfofsky/archive/2011/07/23/2115129.html

附：自己的一个随机排序

// 随机排序一维数组

private void RandomSort(Integer[] arr) {
int temp = 0;
int rand = 0;
int tempLen = arr.length;
// 将数组进行随机排序
        for (int i = 0; i < tempLen; i++) {
            rand = (int) (Math.random() * tempLen) + i;
if (rand >= tempLen) {
                rand = tempLen - 1;
            }
            temp = arr[i];
            arr[i] = arr[rand];
            arr[rand] = temp;
        }  
}