3D光栅化与2D光栅化在图元绘制方面差别并不大，3D光栅化主要是多了很多坐标系(Local，world，View...)，除此外遮挡算法和裁剪算法也会稍微复杂一些。

本篇文章的重点就主要集中在各种坐标系变换上。

1.基本3D变换

本文所采用的向量(vector)表示为行主序(Row Major)，向量与矩阵(matrix)相乘方式为左乘(left or pre-multiplication)，向量与矩阵相乘表示如下：

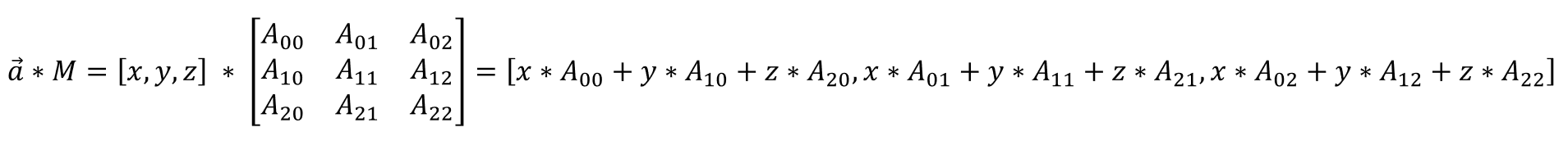
a.缩放变换(Scale)

缩放变换即对一个三维向量的x，y，z分量分别进行缩放，三维向量a在x，y，z方向上进行缩放操作可以表示为：

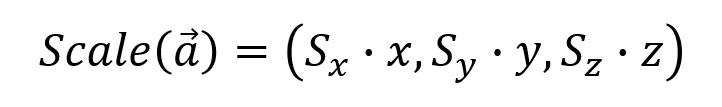
考虑到使用向量和矩阵相乘实现缩放变换，可知：

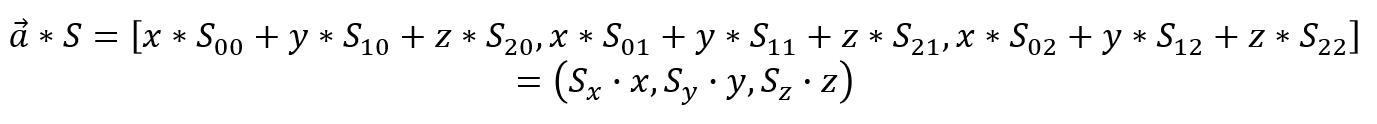
可以得出

，

，

，则缩放变换的矩阵表示形式为：

缩放变换的逆变换的矩阵表示形式为：

b.旋转变换(Rotation)

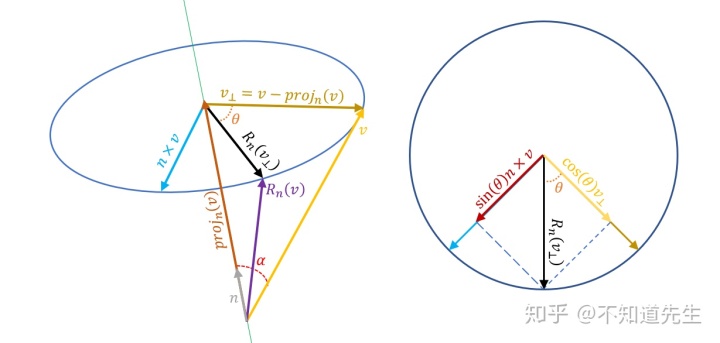
如上图，向量

以单位向量

为轴旋转角度

，得到旋转后的向量

，

与

之间的夹角为

，

为

在

方向上的投影向量，则旋转后向量

可以表示为：

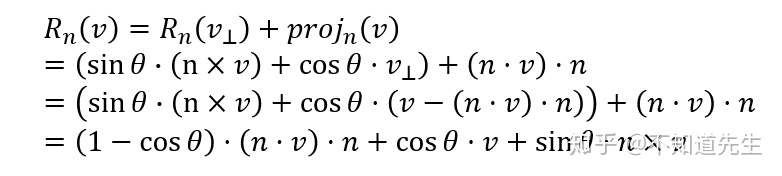
令

，

，则：

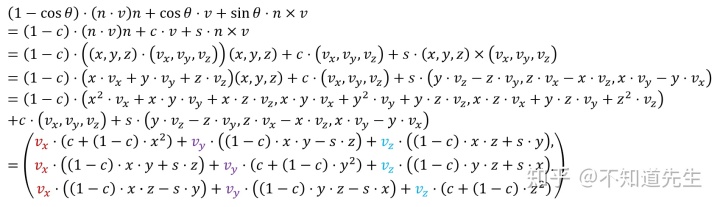
将上式中的参数带入到矩阵中即可到旋转变换的矩阵表示：

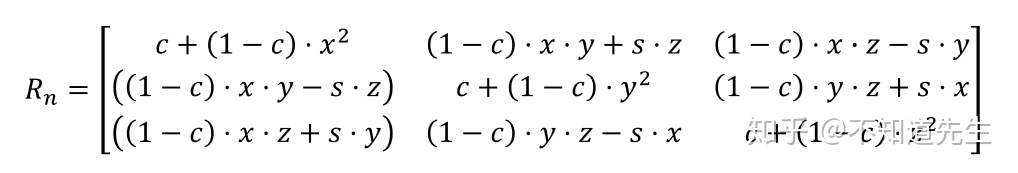
由于

为正交矩阵(各行，各列为单位向量，且两两正交)，因此

，旋转变换的逆变换为：

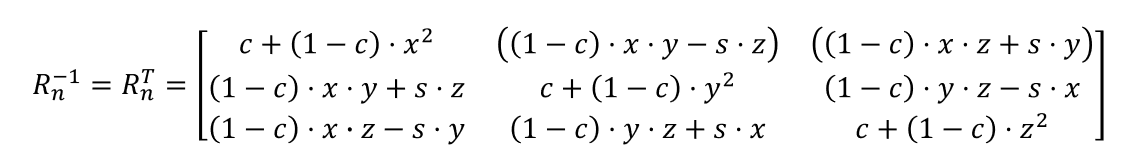
特别地，当

为x,y,z轴时(即：

，

，

)，旋转矩阵分别为：

c.平移(Translation)

3D空间中的点和向量都可以用三维向量表示，前面所介绍的缩放和旋转变换对向量都适用，但平移变换对向量并无意义(平移后的向量与原向量完全相同)，然而3D空间中的点却可适用平移变换。为了区分点和向量，同时一致地对它们进行表示，我们可以采用齐次坐标(homogeneous coordinates)，即：

• 当表示向量时其坐标为：
  ，
• 当表示点时其坐标为：

使用齐次做表时对应的缩放和旋转矩阵为(齐次坐标为1x4向量，应与4x4矩阵相乘，矩阵第四列为[0,0,0,1]，保证相乘后点和向量的w分量保持不变)：

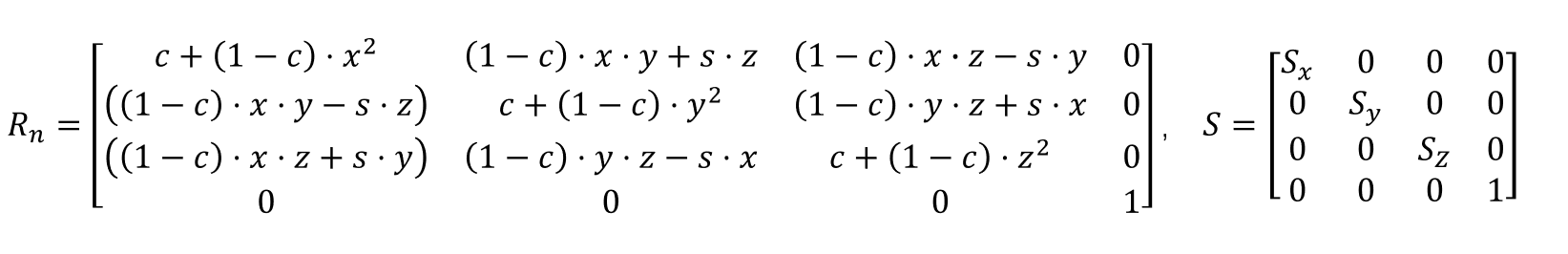
对空间中一点

施加平移变换

可表示为：

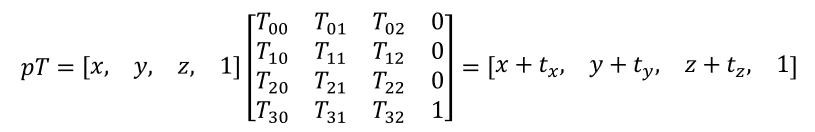
由矩阵和向量相乘运算规则可以知：

,

,

，

，

，

。因此平移变换的矩阵表示为：

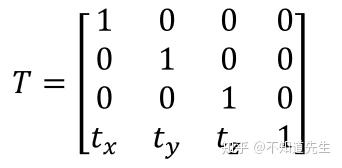
平移变换的逆变换矩阵表示形式为：

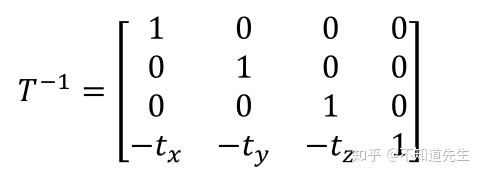
d.基本变换组合

可以将三种基本变换组合起来表示更复杂的变换，如：

表示对点

先后进行缩放，旋转和平移变换，但不同组合顺序的基本变换会得到完全不同的复杂变换。

已知点

，缩放变换

(x,y,z分量分别缩放7,5,3)，旋转变换

(绕y轴旋转45度)和

(沿x,y,z方向分别平移6,2,4)，则对点

施加

变换后得到点

，对点

施加

则得到的点

。因此在组合基本变换时需要注意运算顺序，本文采用的组合顺序为

(先缩放，然后旋转，最后平移)。

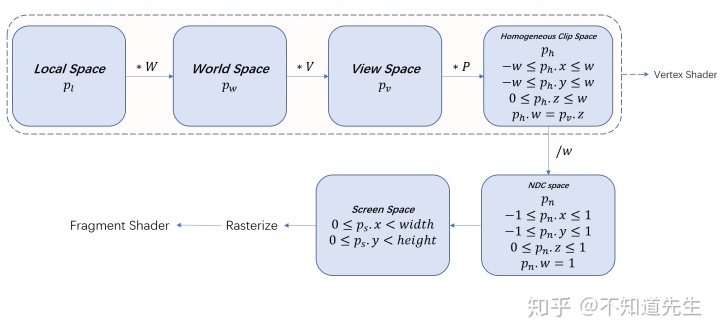
2.3D坐标系变换

本文采用的坐标系规范与DirectX相同(左手坐标系)，如下图所示：

已知坐标系A和坐标系B，坐标系B的x，y，z轴在坐标系A下可表示为

，

，

，坐标系B的原点在坐标系A下表示为

。

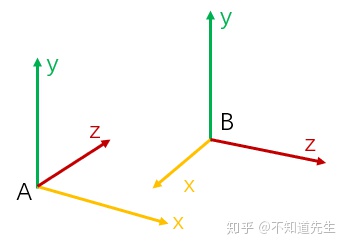
则将坐标系B中一点

从坐标系B变换到坐标系A的变换矩阵为:

变换过程中点

在空间中的位置并没有发生改变，只是参考坐标系发生了改变，从B坐标系变到A坐标系。(缩放，旋转，平移变换只有在同一坐标系下才有意义。)

a. 本地空间(Local Space，Local Coordinate System)

3D渲染中用到的每个模型都有自己的本地坐标系，因为每个模型都在独立的坐标系中进行建模，所以本地坐标系也被称为模型坐标系(model space)。使用本地坐标系有如下好处：

• 建模更加方便，每个模型在自己的本地空间的中央进行建模，不同模型之间互不干扰。
• 建好的模型可以被应用到多个场景(多个不同坐标系中)，而不用对模型做任何改动。
• 有利于大规模的重复的实例绘制(instance)。

b. 世界空间(World Space，World Coordinate System)

在本地坐标系中建好的模型都会经过缩放，旋转，平移等操作后变换到世界坐标系中的不同位置构成渲染场景。

模型一开始放置在世界坐标系中时，其本地坐标系与世界坐标系重合，经过一系列缩放，旋转，平移变换后被放置在世界坐标系中的适当位置构成渲染场景，经过变换后的Local Space的x，y，z轴及原点在World Space下表示为

，

，

及

。则从本地坐标系到世界坐标系的世界变换

可以表示为：

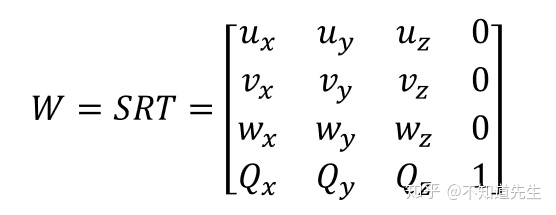
可以通过世界变换将本地坐标系中的点转换到世界坐标系中，即

。

c. 观察空间(View Space，View Coordinate System)

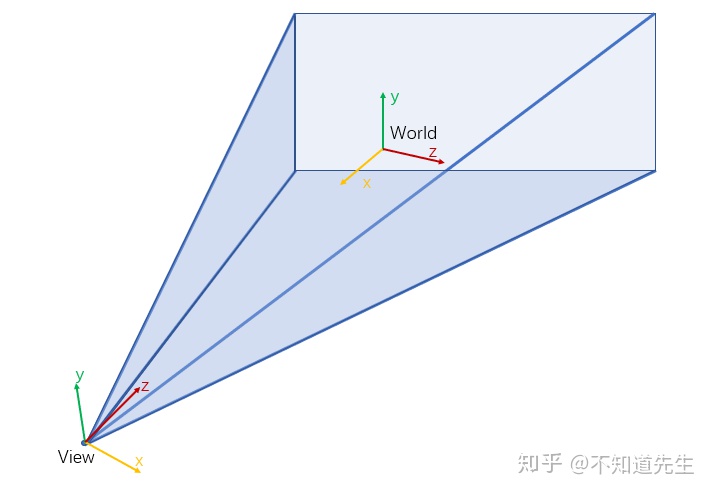
有了场景之后，还需要在场景中放置一个虚拟的摄像机才能在场景中实现漫游，以摄像机的角度来观察游戏场景。此时可以为摄像机附加一个坐标系，相机所看的方向为坐标系z轴，x轴指向相机的右侧，y轴指向相机的上方，这个附加在相机上的坐标系即为观察坐标系(相机坐标系)。

相机能够将可视范围内的3D场景转化为2D图像(不在view volume内的物体可以直接剔除)。

若观察坐标系的x,y,z轴以及原点在世界坐标系下可以表示为：

，

，

及

，则可以得到从观察坐标系到世界坐标系的变换

:

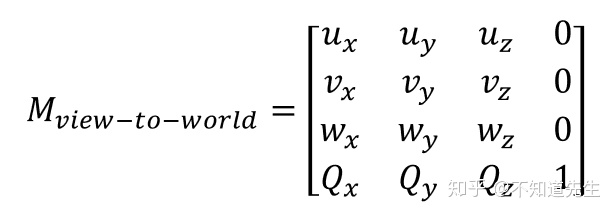
但我们需要的是观察坐标系到世界坐标系的逆变换，即世界坐标系到观察坐标系的变换

。而从世界坐标系到观察坐标系的变换只涉及到旋转和平移变换，则

又可以表示为

。因此从世界坐标系到观察坐标系的变换

可以表示为：

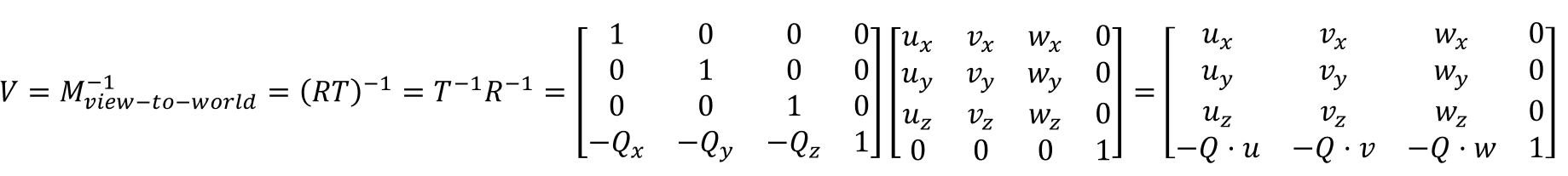
d. 齐次裁剪空间与归一化设备坐标系(Homogeneous Clip Space and Normalized Device Coordinates)

现在需要将相机可视范围内的物体投影到2D平面上，相机的可视范围可以用一个处于近平面(near plane)与远平面(far plane)之间的平截棱锥(view frustum)表示：

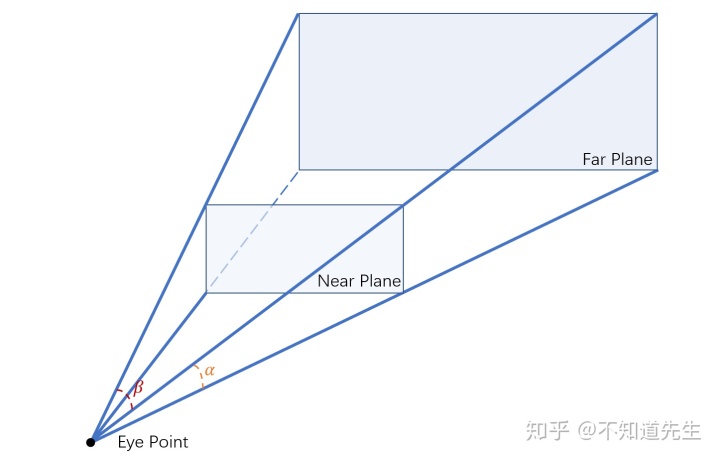
这里采用view frustum的near plane作为投影平面，由于从3D场景投影转换为2D图像后会损失一个维度，因此在投影过程中还需要保留物体在view space中的z值来判断物体之间的遮挡关系。如下图：

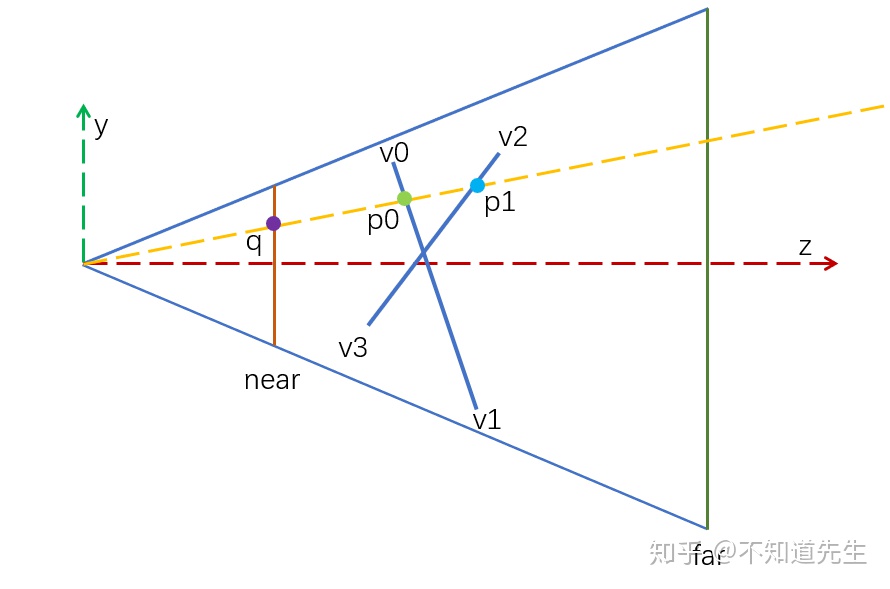
空间中的两点p0，p1经过投影后都位于near plane上的q点，需要根据p0，p1在view space中的深度值(z值)来判断应该绘制p0还是p1点。因为需要保存深度值到缓存中，并根据深度值来判断空间物体遮挡关系，这种遮挡算法就被称为z-buffer。

PS:虽然原理上是使用View Space的z值进行遮挡判断，但其实DirectX的z-buffer里存储的是NDC Space的z值。z-buffer是单通道的图片，可以用一个Image<float>对象表示。

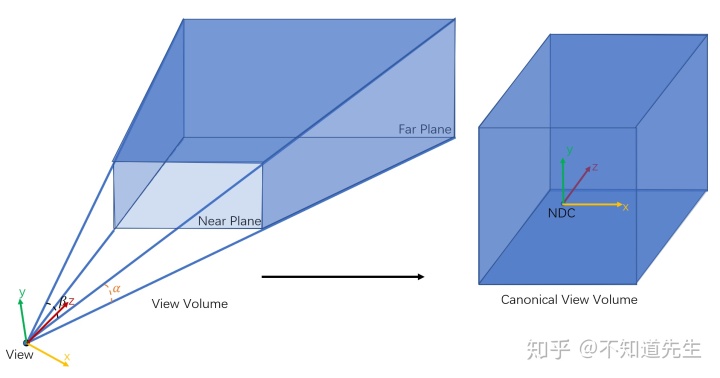
投影的同时还需要对穿过view frustum的图元进行裁剪，为了方便裁剪，可以将view frustum变换成为一个长方体，这样就可以更快捷的判断图元与view frustum的关系。经过变换后的view frustum被称为canonical view volume(CVV)。处在CVV内的点

满足一下关系：

经过变换后CVV所处的坐标系就被称为归一化坐标系(Normalized Device Coordinates，NDC)(裁剪，投影都是在这一变换过程中进行的)。

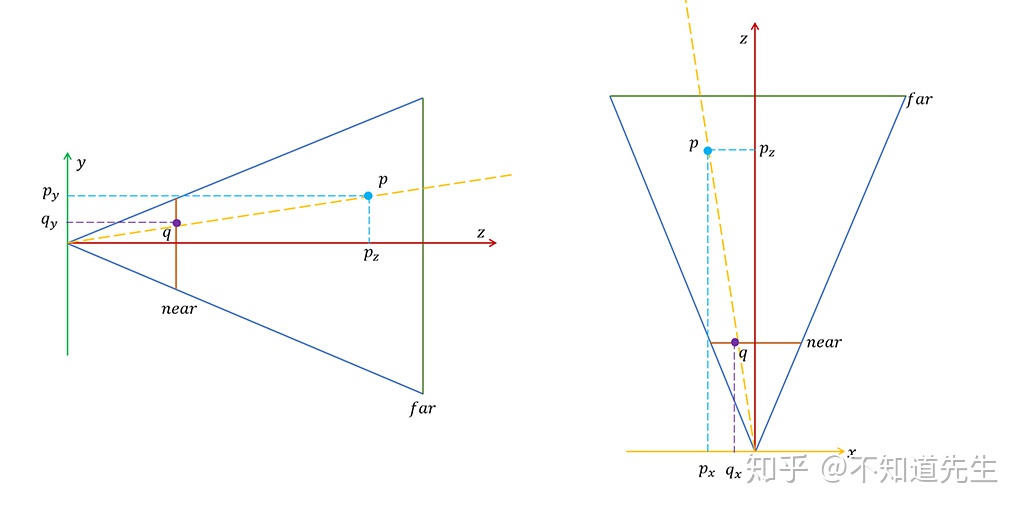
已知View space中的一点

，要将其投影到near plane(

)上，投影到2D平面后的点为

，且near plane的宽度和高度分别为

和

，由几何关系可知：

投影后的点

位于near plane内，因此满足：

经过以下变换后可满足CVV内点坐标的要求:

由于以上变换为非线性变换的，因此无法用矩阵表示，可以将上诉变换拆分为两个部分：线性部分和非线性部分，非线性部分表示为除以

(透视除法)。这时将点

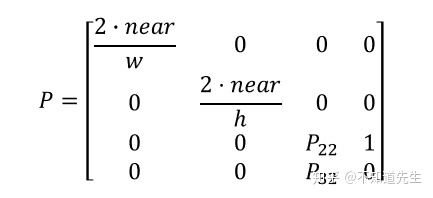
变换到CVV内点

的变换

可以表示为：

CVV内点

可以表示为 :

现在还需要将点

的

坐标变换到CVV坐标范围内，位于view volume点

的

坐标满足 ：

经过变换

变换到NDC空间后的点

的坐标满足:

• 时
• 时

由矩阵与向量运算规则可知：

则：

可以解出

，

因此变换矩阵

可以表示为：

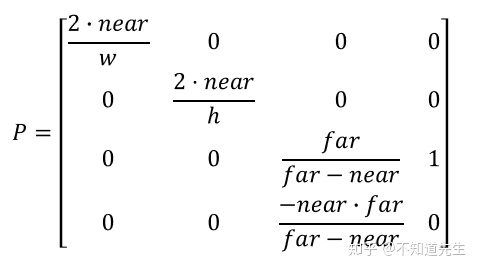
PS：投影矩阵还有其他推导和表示形式，使用参数不同但效果相同。

整个投影变换包含两个部分：

• (透视除法)

若投影变换前的点

的深度值(z)为0，则进行透视除法时会出现除0的情况，为了避免除0，必须在透视除法之前对穿过w=0平面的图元进行裁剪，而在透视除法之前的空间就被称为

在齐次裁剪空间中位于view frustum内的点

满足:

由于每个顶点的z值不同，所以图元中每个顶点在齐次裁剪空间中的clip volume大小也完全不同。

e. 屏幕空间(Screen Space)

最后位于view frustum内的图元经过了前面一系列变换后，将会被变换到屏幕空间(2D坐标系)中进行光栅化。此坐标系与上一篇2D光栅化所使用的屏幕空间坐标系相同：

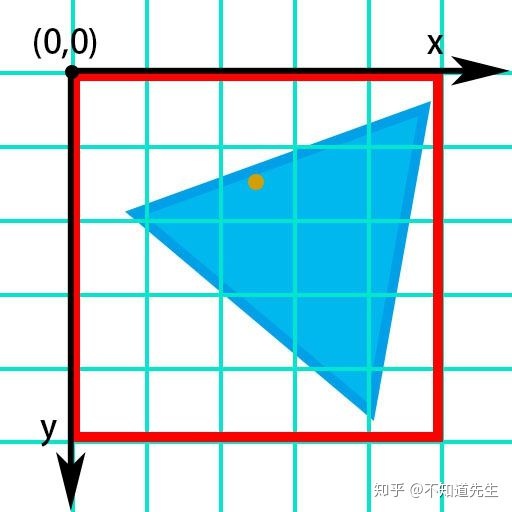
此2D坐标系以Viewport左上角为原点，处于Viewport中的点

的坐标范围为：

可以通过如下变换将NDC空间内的点

变换到屏幕空间中(由于screen space的y轴与NDC space 的y轴相反，所以需要反转y轴)：

f. 坐标系变换总览

3. 3D光栅化

3D光栅化发生在图元被变换到Screen space之后，因为这里的Screen space与2D的Screen Space完全一致，所以2D的光栅化算法在这里也依然适用。

然而由于图元经过了投影变换，且投影变换为非线性变换，所以不能用简单的线性插值来获取fragment的属性。

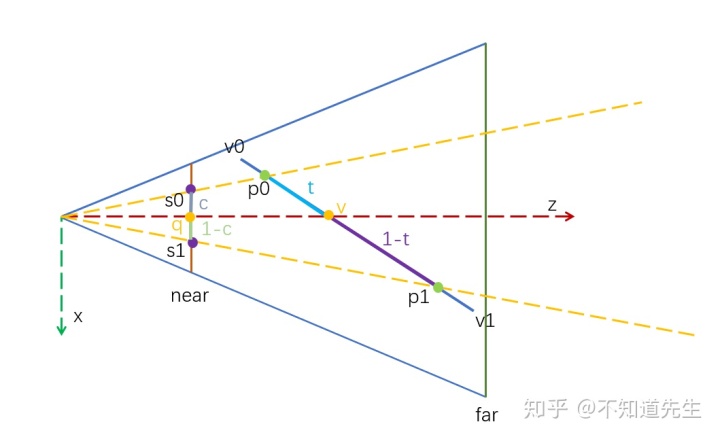
如上图所示，view space中的线段v0v1上两点

，

在near plane上的投影为点

，

。

，

中间一点

在near plane上的投影为点

。从图中可以看出点v到p0，p1的距离比值与点q到s0，s1的距离比值完全不同，投影变换不保持距离不变。

为了执行z-buffer算法，需要通过点

获取到点

的深度值(z)。

点

的深度值可以通过如下方法插值得到：

证明如下：

由于点

为点

在near plane上的投影，因此点

与点

的关系为：

且

位于

之间，则：

• 式(1)

由点

在

，

之间， 点

在

，

之间则有：

带入式(1)可得:

式(2)

又s0和s1分别为p0和p1在near plane上的投影，则：

带入式(2)可得：

化简得：

则：

带入式(1)可得：

则若View space中三角形

，变换到Screen Space后为三角形

，

内一点

在Screen Space的投影为

内的点

，对三角形

内的点(fragment)

,可以通过如下方法取得fragment

在View Space中对应的深度值:

为点

在三角形

内的重心坐标。

执行z-buffer算法时，若当前光栅化的点

(fragment or pixel)的深度值小于z-buffe中点

处对应位置的深度值，则当前光栅化的点未被遮挡，可以将点

的深度值写入到z-buffer，并对

进行着色 (shading)操作。

在对点进行shading时还需要点的其他属性值(纹理坐标，点的颜色，法线等...)

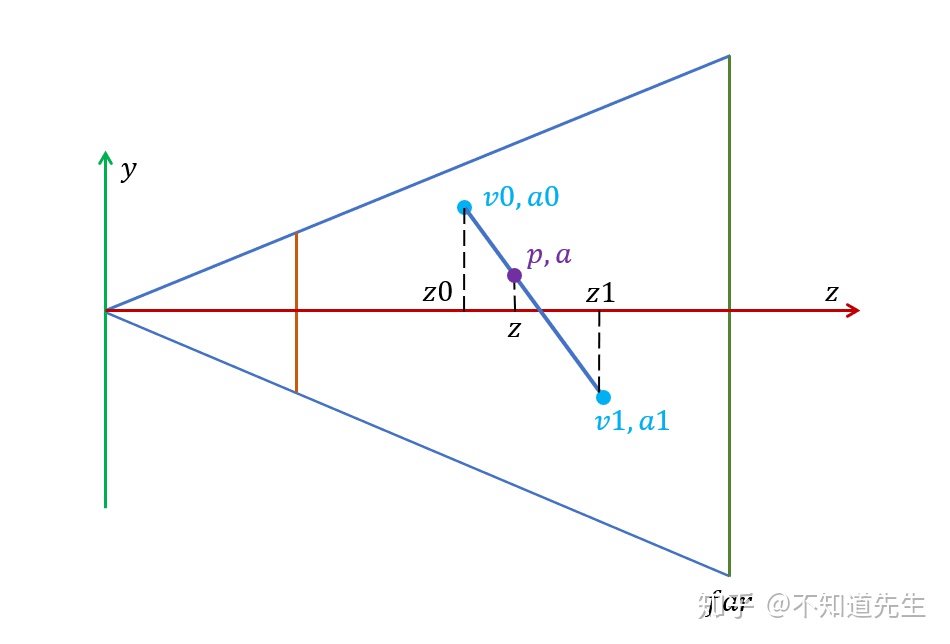
如上图已知view space中，三角形两边上两点

和

对应深度值和属性值分别为

，

和

，

，则线段

内一点

的深度值和属性值为

，

,由线性插值可知深度值与属性值存在的关系为：

式(3)

且点

的深度值与

，

的深度值存在的关系为：

带入式(3)可得：

则 :

可得对Screen space三角形

内一点

的任意属性插值的公式为：

为点

的重心坐标，

分别为

在view space中对应点的深度值。

PS:可以用这个方法插值得到

在NDC Space内对应点的深度值。

整个3D光栅化算法可以由如下伪代码表示：

// Local space
Triangle tri;// *W ，变换到World Space
TransformToWorldSpace(tri, W);// *V ，变换到View Space
TransformToViewSpace(tri, V);// *P ，变换到Homogeneous Clip Space
TransformToHomogeneousClipSpace(tri, P);// 在Homogeneous Clip Space进行裁剪和剔除
Clip(tri);// 除以w分量 ，经过透视除法后变换到NDC Space
PerspectiveDivide(tri);// 获取三角形顶点在Screen Space中的坐标
screen_space_triangle = GetScreenSpacePositon(tri);// 进入Screen Space后就可以同2D一样可以采用Half-Space光栅化算法
{//获取Screen Space三角形的包围盒GetBoundingBox(screen_space_triangle, box_min, box_max);//遍历包围盒中的fragmentfor (fragment(or pixel) in BoundingBox){//用PrepDotP判断fragment是否在三角形中，if (fragment in screen_space_triangle){//若fragment在三角形中，则计算fragment的重心坐标用于插值GetBarycentricCoordinates(λ0, λ1, λ2);//插值获得fragment在View Space中的深度值view_z = GetViewSpaceZ();//再次插值获得fragment在NDC Space中的深度值ndc_z = GetNDCSpaceZ(view_z);//若当前光栅化的fragment的深度值小于Z-Buffer中对应位置的fragment的深度值，则当前fragment未被遮挡if (ndc_z < ZBuffer(fragment.pos)){//插值当前fragment的属性(normal,uv...)InterpolatedAttributes(fragment);//着色Shading(fragment);}}}
}

光栅化部分的代码可以参考2D光栅化篇。

4. 3D裁剪

3D裁剪发生在齐次裁剪空间。齐次裁剪空间中CVV内的点需要满足一下要求：

可以在裁剪之前对不在CVV内的三角形直接剔除(三个顶点均不在CVV内)，只需要对穿过CVV的三角形进行裁剪（裁剪方法与2D裁剪相似）。

CVV由6个面组成(left，right，top，bottom，near，far)，每个面将空间分为两个区域，因此可以用6bit二进制编码对这些区域进行编码。对齐次裁剪空间内一点

，若：

• ，则点在left裁剪平面外侧，第一位编码为1；
• ，则点在right裁剪平面外侧，第二位编码为1；
• ，则点在bottom裁剪平面外侧，第三位编码为1；
• ，则点在top裁剪平面外侧，第四位编码为1；
• ，则点在near裁剪平面外侧，第五位编码为1；
• ，则点在far裁剪平面外侧，第六位编码为1；

对三角形进行裁剪时，先根据三角形三个顶点的Clip Code判断三角形与裁剪平面的关系，然后再采用Sutherland–Hodgman算法对三角形进行裁剪。

若采用Half-Space光栅化算法则只需要对near裁剪平面进行裁剪即可(防止透视除法时除0，在near plane上的点w=camera space z=near。由于Half-Space算法只处理三角形包围盒与Viewport交集内的fragment，所以left，right，top，bottom裁剪平面可以不做处理)。

对齐次裁剪空间内的线段

若其穿过near裁剪平面，则其与near裁剪平面的交点

满足：

即：

由于

位于near裁剪平面上，有

，可以求出

，进而求出交点

的坐标。

下面给出使用Sutherland–Hodgman算法对穿过near plane的三角形进行裁剪的代码(Sutherland–Hodgman的介绍可以参考2D篇)：

void 

其他裁剪平面的处理与near plane相似(更完整的裁剪代码可以参考我的光栅化项目)

到这里为止整个3D光栅化的流程也就结束了，有了fragment插值后的属性即可进行光照着色，渲染相关的内容这里就不再提及了。

Tips1：背面剔除(Backface Culling)

根据使用的光栅化算法的不同可以选择在不用的坐标系中进行背面剔除。

如果使用Scan-Line算法，则可以在齐次裁剪空间或者NDC Space进行背面剔除，在这两个空间中是以相机观察方向为z轴。可以用叉乘求出三角形的面法线，然后用面法线和z轴做点乘，判断三角形面是否为背面。

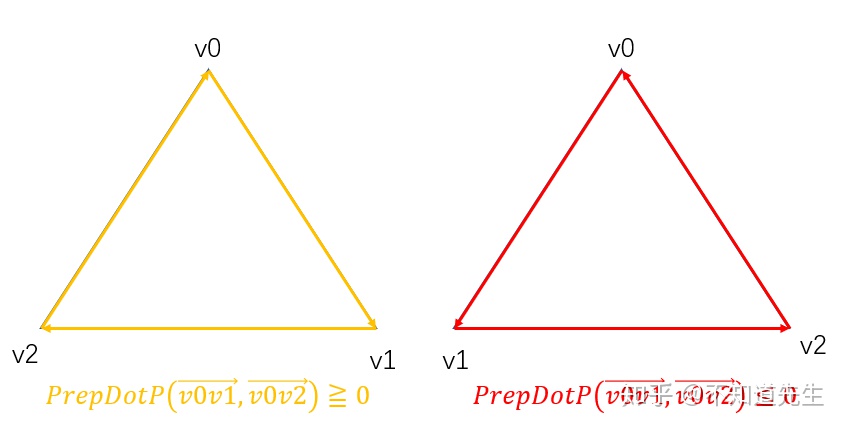
若使用Half-Space算法，则可以在转换到Screen Space之后，光栅化之前做背面剔除。可以使用PrepDotP(Edge Function)求三角形的面积，当顶点为顺时针时则PrepDotP大于

0，逆时针则小于0。可以借此判断三角形是否为背面。

Tips2：Top-Left rule

对于有共享边的相邻三角形，会对共享边进行重复光栅化。

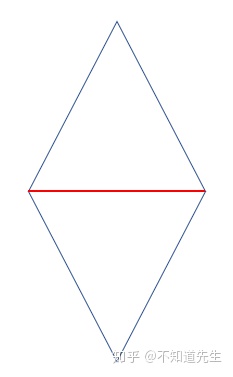
为了解决共享边的重复绘制，可以采用Top-Left rule，对三角形的top边和Left边不进行光栅化。

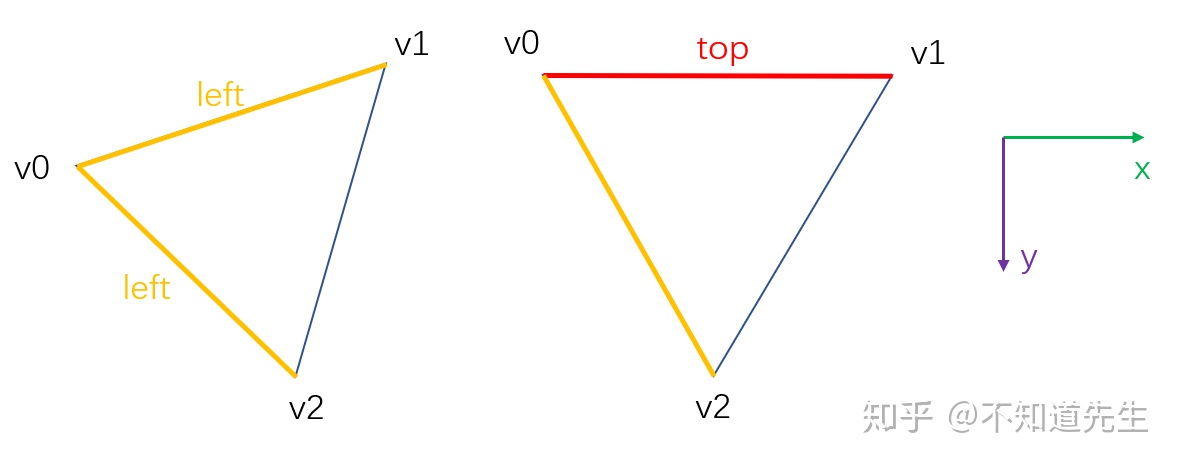
对三角形的任意一条边V[i]V[(i+1)%3]，若：

• V[(i+1)%3].x-V[i].x >0 且 V[(i+1)%3].y-V[i].y = 0则为top edge(如第二个三角形的v2v0边)。
• V[(i+1)%3].y-V[i].y < 0则为left edge。

Top-Left rule可以和PrepDotP结合起来判断是否应该对当前的fragment进行光栅化(fragment 在三角形内，且不为top or left edge)。