2023.8.6

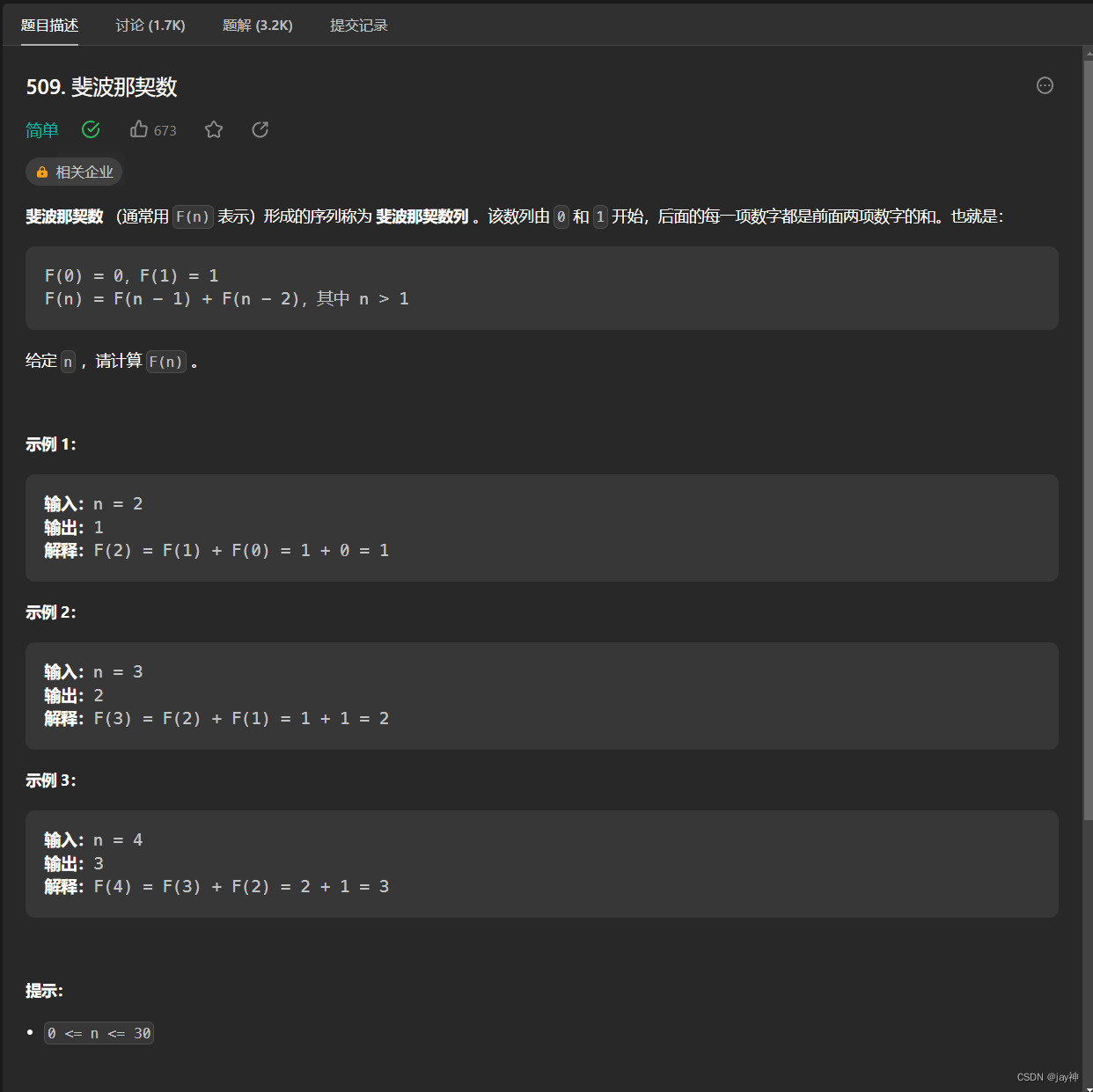
         明天放假回长沙了，回家先玩几天。  今天开始刷动态规划的题目了，先拿道简单的练练手。由于本题提示中说n在30以内，所以我是构造了一个大小为30的int型哈希数组，然后将30以内的斐波那契数列全部放入数组中，然后返回对应n的数值。 代码如下：

class Solution {
public:int fib(int n) {int hash[31];hash[0] = 0;hash[1] = 1;for(int i=2; i<=30; i++){hash[i] = hash[i-1] + hash[i-2];}return hash[n];}
};

        按照动态规划的步骤来分析的话：

1. 确定dp数组以及下标的含义：dp[i]的定义为：第i个数的斐波那契数值是dp[i]
2. 确定递推公式：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]
3. dp数组如何初始化：dp[0]=0,dp[1]=1;
4. 确定遍历顺序:从前往后
5. 举例推导dp数组：dp数组应该是如下的数列：0 1 1 2 3 5 8 13 21 34 55

        按照此思路的代码如下：

class Solution {
public:int fib(int n) {vector<int> dp(n+1);if(n<=1) return n;dp[0] = 0;dp[1] = 1;for(int i=2; i<=n; i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};