221. 最大正方形

题目描述：
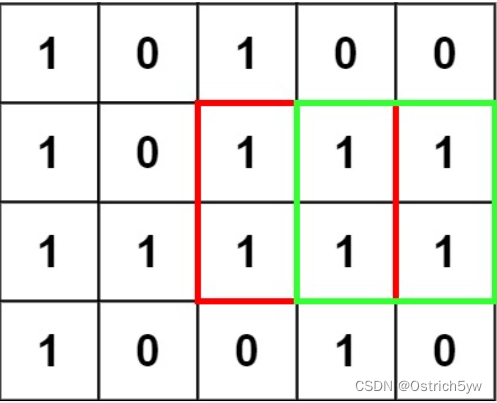
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

考察重点：动态规划

方法概括：二维矩阵中查询最大矩形 dp[i][j] = Min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) + 1 也可以使用暴力算法：向右下遍历

func findMin(a, b, c int) int {temp := aif temp > b {temp = b}if temp > c {temp = c}return temp
}
func MaximalSquare(matrix [][]byte) int {var recmatrix [][]int //负责记录每一个点可以达到的最大面积for i := 0; i < len(matrix); i++ {t := make([]int, len(matrix[0]))recmatrix = append(recmatrix, t)}var max int = 0for i := 0; i < len(matrix); i++ {for j := 0; j < len(matrix[0]); j++ { //遍历所有节点	查找他左侧，上侧，左上侧节点可以达到的最大面积进行比较if matrix[i][j] == '0' {continue}if i == 0 || j == 0 { //边缘节点必定为1recmatrix[i][j] = 1if recmatrix[i][j] > max { //考虑 0 1 的情况max = recmatrix[i][j] //	  1 0}continue}/**状态转移方程dp[i][j] = Min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) + 1*/recmatrix[i][j] = findMin(recmatrix[i-1][j], recmatrix[i][j-1], recmatrix[i-1][j-1]) + 1if recmatrix[i][j] > max {max = recmatrix[i][j]}}}return max * max //返回面积
}
##################暴力解法######################
func decima(matrix [][]byte, i, j int) int {var k int/**从a开始 k为向外步数，此处为1-3k=1遍历b，k=2遍历c，k=3遍历d..........a b c d..b b c d..c c c d..d d d d..........*/for k = 1; k < len(matrix)-i && k < len(matrix[0])-j; k++ {for i1 := i; i1 <= i+k; i1++ { //列不动，遍历行(纵向)if matrix[i1][j+k] == '0' {return k - 1 //如果有一个参数不为1，直接返回k-1(这一轮不符合要求，说明上一轮符合要求)}}for j1 := j; j1 <= j+k; j1++ { //行不动，遍历列(横向)if matrix[i+k][j1] == '0' {return k - 1}}}return k - 1
}func MaximalSquare(matrix [][]byte) int {var max int = 0for i := 0; i < len(matrix); i++ {for j := 0; j < len(matrix[0]); j++ { //遍历所有节点if matrix[i][j] == '0' {continue}temp := decima(matrix, i, j) + 1 //若当前结点为1，则向他右下方遍历。走k-1步为矩形，说明矩形大小为(k-1) + 1if temp > max {max = temp}}}return max * max //返回面积
}