集合属性注入值

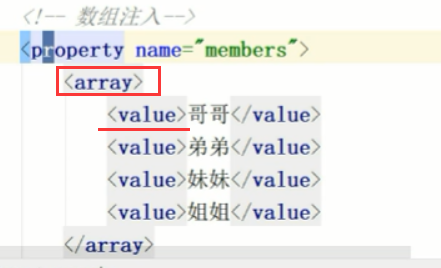
一、集合注入，装配bean的时候，即在xml中添加bean的时候

1、List集合

 

 2、set集合，无序，即无索引，所以也无重复，

 

 3、map key-value键值对双列集合，内置接口Entry

 

 4、Properties集合，可以和IO流结合读写文件的集合；

 

 5、数组注入

 

转载于:https://www.cnblogs.com/wmqiang/p/11564776.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/262684.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

QuerySyntax（查询语法）

QuerySyntax（查询语法）

Code/// <summary>/// QuerySyntax&#xff08;查询语法&#xff09;的摘要说明/// </summary>public class QuerySyntax { public int ID { get; set; } public string Name { get; set; } public void QuerySyntaxTest() { List<Quer…
阅读更多...
二、ceph编译源码、单机搭建调试环境

二、ceph编译源码、单机搭建调试环境

2019独角兽企业重金招聘Python工程师标准>>> 准备一台机器&#xff1a; roottest3:~# cat /proc/version Linux version 3.13.0-32-generic (builddkissel) (gcc version 4.8.2 (Ubuntu 4.8.2-19ubuntu1) ) #57-Ubuntu SMP Tue Jul 15 03:51:08 UTC 2014 一、下载ce…
阅读更多...
C#与Unity 数据存储

C#与Unity 数据存储

使用Json存储数据 1.创建Json文件&#xff0c;直接创建txt文件&#xff0c;将后缀名改为xx.json 2.Json文件的数据格式&#xff0c;中括号表示列表&#xff0c;即中括号下的每个逗号隔开的内容都是列表的每个元素&#xff0c;花括号表示对象&#xff0c;冒号前面的表示属性名&a…
阅读更多...
centos linux 系统日常管理4 scp,rsync,md5sum,sha1sum,strace ,find Rsync 常见错误及解决方法 第十七节课...

centos linux 系统日常管理4 scp,rsync,md5sum,sha1sum,strace ,find Rsync 常见错误及解决方法 第十七节课...

centos linux 系统日常管理4 scp,rsync,md5sum,sha1sum,strace ,find Rsync 常见错误及解决方法 第十七节课 rsync可以增量同步&#xff0c;scp不行 注意&#xff1a;修改sshd_config文件时候&#xff0c;port字段&#xff0c;sshd不支持监听小于1024 &#xff0c;1~1023不允…
阅读更多...
注解@Component方式代替xml装配bean

注解@Component方式代替xml装配bean

一、Component 用注解来装配bean 1、 2、对类使用注解&#xff0c;装配bean&#xff1a; 3、类中&#xff0c;注入其他对象&#xff1a; 二、bean.xml中配置Componet方式装配bean 1、开启注解装配bean依赖注入方式和类使用的自动注入 2、 其中&#xff0c;通过类型获取对象时候…
阅读更多...
ASP.NET2.0数据操作之创建业务逻辑层

ASP.NET2.0数据操作之创建业务逻辑层

导言 本教程的第一节所描述的数据访问层&#xff08;Data Access Layer&#xff0c;以下简称为DAL&#xff09;已经清晰地将表示逻辑与数据访问逻辑区分开了。不过&#xff0c;即使DAL将数据访问的细节从表示层中分离出来了&#xff0c;可它却不能处理任何的业务规则。比如说&a…
阅读更多...
不使用注解和使用注解的web-service-dao结构

不使用注解和使用注解的web-service-dao结构

一、未使用注解的web-service-dao结构 1、action类源码 其中&#xff0c;service作为一个成员属性&#xff0c;采用的是层层调用&#xff0c;service类中dao作为一个成员属性&#xff0c;再成员方法中调用&#xff1b; 2、bean.xml中装配bean&#xff1a; 3、创建spring容器&am…
阅读更多...
awk特殊用法

awk特殊用法

一、从固定格式中取出IP所在的class&#xff0c;并列出例&#xff1a;class A { 192.168.1.1 192.168.2.1 192.168.3.1 192.168.169.69}class B { 192.168.1.1 192.168.169.69}sed -nr /\{/{:1;N;/\}/!b1;/192.168.169.69/s#^([^{]).*#\1#p} fileawk -vRScla…
阅读更多...
XML基础——extensible markup language

XML基础——extensible markup language

一、xml概念 1、xml和html区别 其中&#xff0c;xml是纯文本文件&#xff0c;跨语言&#xff1b;浏览器有html解析器也有xml解析器&#xff1b; 2、和properties配置文件区别 二、xml语法 1、基本语法 三、xml组成部分 中国电脑默认GBK编码格式&#xff08;中文编码&#xff09…
阅读更多...
显示单选列表对话框

显示单选列表对话框

通过AlertDialog.Builder类的setSingleChoiceItems方法可以创建带单按钮的列表&#xff1a;方法如下&#xff1a;1、从资源文件中装载数据&#xff1a;public Builder setSingleChoiceItems(int itemsId, int checkedItem, final OnClickListener listener)2、从数据集中装载数…
阅读更多...
全修CALL

全修CALL

PUSH -1PUSH 0PUSH 0CALL 005A8690ADD ESP,0Cbp send,点全修CTRLf9一直返回到没有参数 基本上这个返回就是 功能CALL 0012EB08 005869B2 返回到 elementc.005869B2 来自 elementc.0058E8A00012EB1C 00588B1F 返回到 elementc.00588B1F 来自 elementc.005869800012EB28 …
阅读更多...
OSChina 周六乱弹 —— 这个版本的小红帽听说过吗？

OSChina 周六乱弹 —— 这个版本的小红帽听说过吗？

2019独角兽企业重金招聘Python工程师标准>>> 想想当年刚出来工作的时候&#xff0c;小小编还真是单纯&#xff0c;以为广阔天地大有作为&#xff0c;可是呢。。。 上热门&#xff1a;刚出来工作的时候&#xff0c;大人千叮万嘱社会很复杂&#xff0c;要学会控制自己…
阅读更多...
XML解析

XML解析

一、解析xml的两种方式 1、 其中&#xff0c;xml文件被解析之后产生的dom树可能是原xml文件内存的成千上万倍&#xff0c;所以占内存&#xff1b;一般是服务器端&#xff1b; 2、sax逐行读取解析的方式&#xff0c;读一行释放一行&#xff0c;移动端采用&#xff1b; 其中&…
阅读更多...
Arcgis Server初学笔记（一）

Arcgis Server初学笔记（一）

什么是Arcgis Server(以下简称AS)&#xff1f; AS是一个基于web的企业级GIS解决方案。AS为创建和管理基于服务器的GIS应用提供了一个高效的框架平台。AS宿主了各种GIS资源&#xff0c;并把他们作为服务发送到客户端。Accgis Server架构 AS是一个分布系统&#xff0c;…
阅读更多...
XML解析——Jsoup解析器

XML解析——Jsoup解析器

一、Jsoup解析器快速入门案例 Docement对象&#xff0c;文本对象&#xff0c;包含着各个Dom树结构 1、引入Jsoup解析器的jar包放在lib文件夹下后&#xff0c;写java代码 其中&#xff0c; 二、Jsoup对象 1、Jsoup解析器解析xml和html的有关对象 其中&#xff0c;通过统计资源定…
阅读更多...
jQuery缓存数据——仿Map

jQuery缓存数据——仿Map

2019独角兽企业重金招聘Python工程师标准>>> 最近在工作中遇到了这样一个情景。有些数据是从后台读取的&#xff0c;但是我暂时不需要展示在页面上&#xff0c;那怎么办呀&#xff1f;——缓存呀。今天我就来分享一下我所了解的Jquery缓存数据的方法。 首先分享1篇博…
阅读更多...
Jsoup快速查询

Jsoup快速查询

一、selector选择器 二、Xpath查询 转载于:https://www.cnblogs.com/wmqiang/p/11568184.html
阅读更多...
Servlet生命周期和方法

Servlet生命周期和方法

一、五个生命周期方法&#xff0c;有三个很重要&#xff0c;初始化方法、提供服务方法和销毁方法 1、三个主要方法 2、另外两个重写的成员方法只做了解 二、生命周期详解 其中&#xff0c;每次刷新页面都是一次对servlet访问&#xff1b; 页面访问&#xff0c;根据域名找到主机…
阅读更多...
Servlet3.0注解配置访问路径和urlParttern配置

Servlet3.0注解配置访问路径和urlParttern配置

一、Servlet用注解配置访问路径 二、IDEA的tomcat相关配置 其中&#xff0c;第一点的配置文件&#xff0c;直接在IDEA的可视化操作界面修改就可以改掉配置文件中内容&#xff1b; 三、urlParttern配置 其中&#xff0c;* 时通配符&#xff0c;优先级最低&#xff1b; 转载于:ht…
阅读更多...
现货黄金入门知识普及一：图形分析之K线理论

现货黄金入门知识普及一：图形分析之K线理论

&#xff2b;线又称阴阳线、棒线、红黑线或蜡烛线&#xff0c;最早起源于日本德川幕府时代的米市交易&#xff0c;经过二百多年的演进&#xff0c;现已广泛应用于证券市场的技术分析中&#xff0c;成为技术分析中的最基本的方法之一&#xff0c;从而形成了现在具有完整形式和分…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023