现货黄金入门知识普及一：图形分析之K线理论

Ｋ线又称阴阳线、棒线、红黑线或蜡烛线，最早起源于日本德川幕府时代的米市交易，经过二百多年的演进，现已广泛应用于证券市场的技术分析中，成为技术分析中的最基本的方法之一，从而形成了现在具有完整形式和分析理论的一种技术分析方法。

Ｋ线根据计算单位的不同，一般分为：日Ｋ线、周Ｋ线、月Ｋ线与分钟Ｋ线。

它的形成取决于每一计算单位中的四个数据，即：开盘价、最高价、最低价、收盘价。

（1）当开盘价低于收盘价时，Ｋ线为阳线（MT4一般用空心线表示）；

（2）当开盘价高于收盘价时，Ｋ线为阴线；(MT4一般用实心线表示) ；

 当开盘价等于收盘价时，Ｋ线称为十字星。当Ｋ线为阳线时，最高价与收盘价之间的细线部分称为上影线，最低价与开盘价之间的细线部分称为下影线，开盘价与收盘价之间的柱状称为实体。

由于Ｋ线的画法包括了四个最基本的数据，所以我们可以从Ｋ线的型态可判断出交易时间内的多、空情况。

当开盘价等于最低价，收盘价等于最高价时，Ｋ线称为光头光脚的大阳线，表示涨势强烈；

当开盘价等于最高价，收盘价等于最低价时，Ｋ线称为大阴线，表示汇价大跌；

当开盘价等于收盘价时，且上影线与下影线相当时，Ｋ线称为大十字星，

表示多空激烈交战，势均力敌，后市往往会有所变化，

当十字星出现在Ｋ线图的相对高位时，该十字星称为暮星；

当十字星出现在Ｋ线图的相对低位时，该十字星称为晨星。

综合Ｋ线型态，其代表多空力量有大小之差别，以十字星为均衡点，阳线为多方占优势，大阳线为多方力量最强，阴线为空方占优势，大阴线为空方力量最强。应该注意的是，投资者在看Ｋ线时，单个Ｋ线的意义不大，而应与以前的Ｋ线作比较才有意义。

反转型态（中长期型态）:

单个Ｋ线可反映出单日的价格强弱变化，但它不能准确地反映出价格在一段时间内的变化趋势。那么，对于一段时间的价格变化，我们不再利用Ｋ线的阴、阳、上、下影线进行判断，而利用Ｋ线连接后所形成的中长期型态再加以判断。Ｋ线的中长期基本型态有：头肩型（头肩顶、头肩底）；双重顶（Ｍ头）；双重底（Ｗ底），圆弧底(顶)形态等。

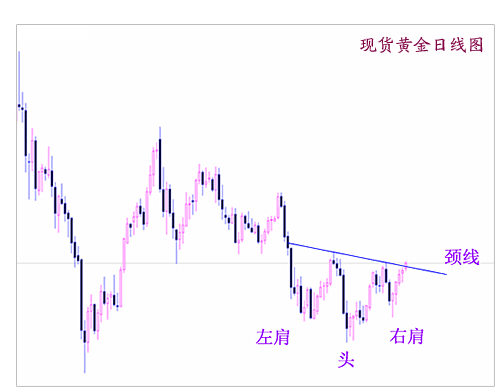
①头肩型

Ｋ线在经过一段时日聚集后，在某一价位区域内，会出现三个顶点或底点，但其中第二个顶点或底点较其它两个顶点或底点更高或更低的型态，这种型态称为头肩型。其中一顶二肩的为头肩顶；一底二肩的为头肩底型。然而，有时也可能出现三个以上的顶点或底点，若出现一个或二个头部（或底部），两个左肩与右肩，称为复合型头肩顶（或复合型头肩底）。