目录

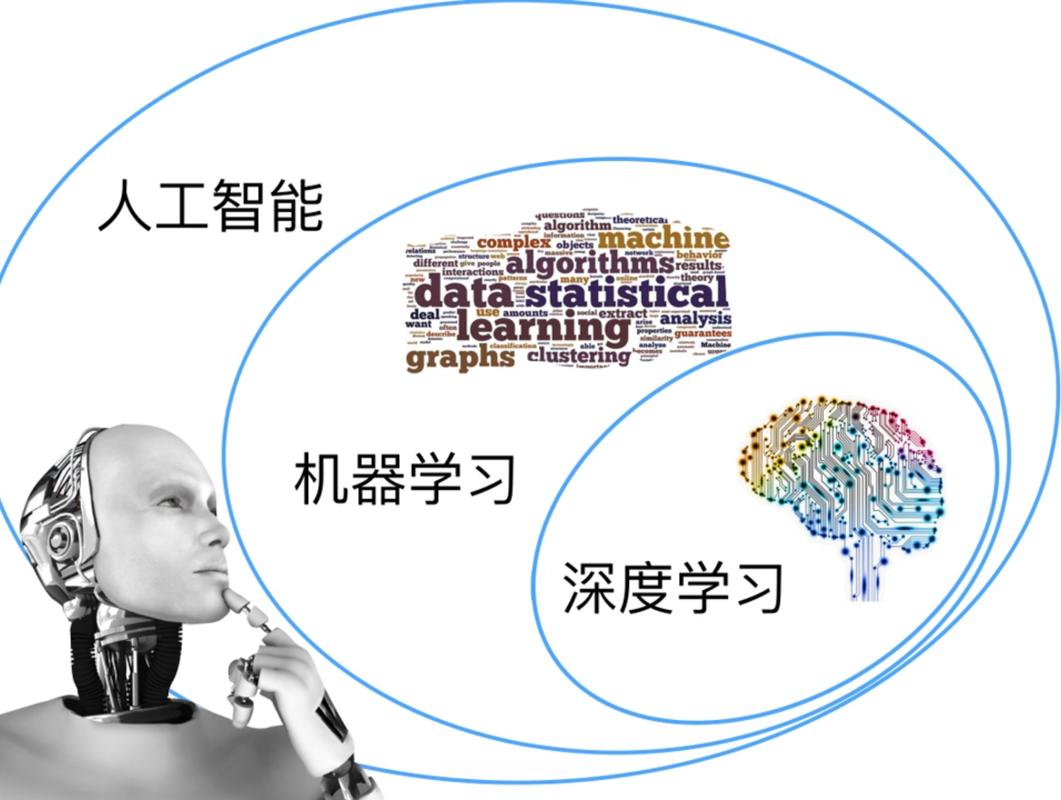
计算机视觉任务

1.K近邻算法

2.得分函数

3.损失函数的作用

4.向前传播整体流程

5.反向传播计算方法

计算机视觉任务

机器学习的流程：

1. 数据获取

2. 特征工程

3. 建立模型

4. 评估与应用

计算机视觉：

图像表示：计算机眼中的图像，而一张图片被表示为三维数组的形式，每个像素的值从0到255。

计算机视觉面临的挑战：照射角度、形状改变、部分遮蔽和背景混入

1.K近邻算法

K(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：在特征空间中，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别。

K近邻计算流程：

1. 计算已知类型数据集中的点与当前点的距离

2. 按照距离依次排序

3. 选取与当前点距离最小的K个点

4. 确定前K个点所在的类别的出现概率

5. 返回前K个点出现频率最高的类别作为当前点预测分类

数据库样例：CIFAR-10

数据库简介：

10类标签、50000个训练数据、10000个测试数据、大小均为32*32

图像的距离计算方式实际上与矩阵的加减法很相似。

K近邻的局限性：不能用来图像分类，因为背景主导是一个最大的问题，我们关注的是主体（主要成分）

2.得分函数

根据得分函数，计算出每个输入的类别得分如下：我们只有类别的得分并不能评判分类效果,损失函数便是用来评估分类效果的好坏程度。

线性函数：从输入--->输出的映射

f(x, W) = Wx

得分函数公式是一种用来描述某种情况下得分的计算方式，一般用于评分、评价等方面。得分函数公式通常由多个参数组成，每个参数代表一种影响因素，通过对这些参数进行加权运算得出最终得分。

3.损失函数的作用

损失函数（loss function）是将随机事件或其有关随机变量的取值映射为非负实数的函数。

在机器学习中，损失函数用于度量模型预测结果和真实结果之间的差距，通常是越小越好。比如在回归问题中，可以使用均方误差（MSE）和平均绝对误差（MAE）等作为损失函数；在分类问题中，可以用交叉熵（CrossEntropy）作为损失函数，或者用二分类问题的二元交叉熵（BCELoss）等。

矩阵来源是优化而来的结果。

神经网络的作用是通过适合的矩阵Wi来处理相应的问题。

做不同任务就是损失函数的不同。

损失函数其实有很多，我们需要的是一个最贴近实际的函数形式。

损失函数：

这里的1相当于是一个近似值的估计。

虽然这两个模型的损失函数值相同，模型A考虑的是局部，模型B考虑的是全局，它们两的侧重方向是不一样的，只是结果恰好相同而已。

损失函数=数据损失+正则化惩罚项(R(W))

我们总是希望模型不要太复杂，过拟合的模型是没有用的。

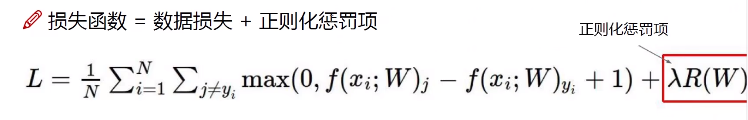
4.向前传播整体流程

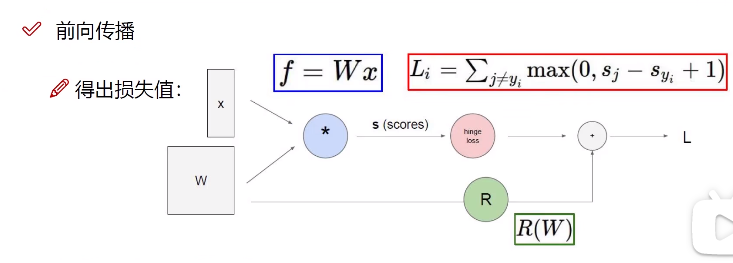
正向传播算法，也叫前向传播算法，顾名思义，是由前往后进行的一个算法。

Softmax分类器

现在我们得到的是一个输入的得分值，但如果给我一个概率值岂不更好！

如何把一个得分值转换成一个慨率值呢？

这和数学建模有共同之处，往往能除以一个相近的函数就能得到一个概率值。

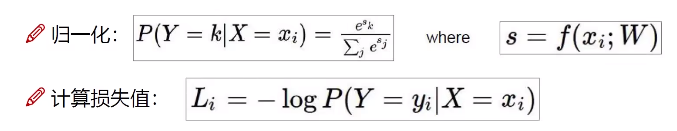
归一化和计算损失值

向前传播：

5.反向传播计算方法

举一个例子：

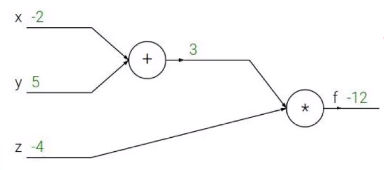
它的函数式是：f(x,y,z) = (x+y)z

q=x+y f=q*z

想要求的值：f对x的偏导，f对y求偏导，f对z求偏导。

这就是我们在高数中学到的链式法则，梯度是一步一步传播的

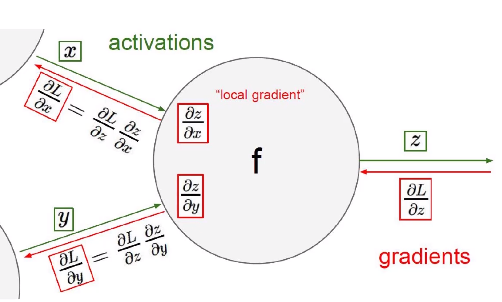
我们所看到的绿色线就是我们上一部分向前传播计算，红色的部分会把上一次的梯度携带到下一层的反向传播的计算中。

反向传播算法，简称BP算法，适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。