二分法求方程的根_快速求解方程的根—

今天是周四高等数学专题的第7篇文章。

之前的文章和大家聊了许多数学上的理论，今天和大家聊点有用的东西。

我们都知道，工业上的很多问题经过抽象和建模之后，本质还是数学问题。而说到数学问题就离不开方程，在数学上我们可以用各种推算、公式，但是有没有想过在计算机领域我们如何解一个比较复杂的方程？

如果之前没有想过，那你可能得想一想，因为以后很有可能会在面试题当中遇到。

二分法

我们要介绍的第一个方法是二分法。

说到二分法大家应该都不陌生，老实说我第一次在高数课本上看到二分法这三个字的时候，其实是蛮震惊的。后来当我又在统计等数学书上看到许多其他算法之后，才慢慢习以为常。在我转行做算法的这几年当中，我越来越意识到，数学的重要性。虽然这并不意味着你一定要成为数学高手，但如果你还没毕业的话，至少数学课好好听讲还是很有必要的。

我们说回二分法，如果学过二分法，会觉得这是一个非常简单的算法，但如果你们做过LeetCode第四题，又会发现纯二分法的题也可以这么难。如果只是单纯地讲解二分法的原理，我们是很难完完全全将这个算法吃透的。为了达到这点，我思考了很久，最终决定仿照看山是不是山的禅宗理论，将二分法也分成三个层次。

首先是第一个层次，即我们每次将一个东西分成两半。

这个应该是我们最初也是最直观的观念，比如最经典的金币问题。说是我们有若干个个硬币，其中有一个是金币，金币的重量更重，其他的硬币重量相等。我们只有一个天平，怎么样用最少的次数找出金币。

在这个问题当中，我们需要不停地将硬币分成两个部分，用天平锁定其中的一个。通过不断重复上述操作，快速找到答案。

在第二个层次当中，二分法不再是简单地将物体一分为二，而是一个折半查找的函数。这也是本文重点要介绍的解方程的方法。

如果有函数 f(x) ，它在区间[a, b]上递增或者递减，并且 f(a)*f(b) < 0。那么我们知道函数必然有一个等于0的解，而且这个解我们可以用二分法来求近似解。

在上图当中，f(x)递增，并且f(a) < 0, f(b) > 0。我们继续获取了a和b的中点 x0。根据上图，我们又得到 f(x0) > 0，所以我们可以把 x0 看成是新的b。于是我们继续寻找a和 x0 的中点，重复上述过程，由于我们最大的误差就是区间的长度，所以当我们区间的长度缩减到足够小，那么就说明我们已经找到了一个足够近似的解。

在二分法当中，我们没进行一次二分迭代，区间的长度就会缩减一半，这是一个指数级的缩减。所以即使一开始的区间很大，经过二分迭代也可以迅速缩减，得到一个非常精准的结果，并且和泰勒级数一样，除了能得到一个足够精确的值之外，还能得到误差的范围。

我们再深入一些思考，会发现有些条件我们还可以再松动松动。比如我们真的需要函数是严格递增或者递减吗？比如我们来看下面这张图：

在(b2, b1)区间内，函数并不是严格递减的，而是先递减再递增的。但是这并不会影响结果的正确性，因为在这个问题当中，二分法并不是通过判断 f(x0) 和a处函数值的大小来缩小区间的，而是通过f(x0)的正负性。也就是说，只需要满足 f(a)*f(b) < 0，并且函数连续且等于0的点只有一个，就可以使用二分来进行查找。

深入思考，就进入了二分法的第三个层次，即放下递增的限制，回到折半这个原始的概念上来。

二分法的本质就是查找空间折半，至于函数递增或者是数组当中元素递增都只是表象，只是我们进行折半的条件。换句话说如果我们能找到其他的条件来折半搜索空间，那么我们一样可以得到二分的效果，并不用拘泥于是否有序。

也就是说我们绕了一圈，最后又回到了将“物体”一分为二这个最基本的概念上来。只是我们经过这么一波折腾，表面上看和最初的理解一样，但其实早已天差地别了。

没想到算法领域也能玩一把禅宗，看山是山，看山不是山，最后回到看山还是山。

牛顿迭代法

看完了二分法，我们再来看另一个快速求根的方法，和二分法一样，它也是迭代逼近的方法，但是逼近的速度更快。这个方法最早是牛顿提出的，因此也被称为牛顿迭代法，我想牛顿这个名字写出来，大家应该都能get到它的分量。

牛顿迭代法的名头看起来很唬人，但是原理真的不难，说白了只有一句话，就是通过切线去逼近，比如我们来看下图：

在上图当中，我们要求 f(x)=0 的根，我们先找到了一个 xn点，我们在 xn 处进行求导取得了它的切线。显然只要这个切线的斜率不为0，那么我们一定可以获得它和x轴的交点。我们将这个交点作为下一个取值，也就是 xn+1的点。我们重复上述过程进行迭代，很快就可以得到一个足够接近的解。

对于点 xn 处的切线而言，它的斜率是 f'(xn)，截距b就是 f(xn)。它的切线方程很好得到，就是：

我们利用这个方程，可以求到它和x轴的交点，也就是xn+1的值：

解下这个方程，可以得到：

上面这个式子就是牛顿迭代法的迭代公式，这是一个非常牛的方法，比二分法要厉害得多，因为它的收敛速度更快，并且计算也并不复杂。

我们来看下它的威力，我们来看知乎鍵山小鞠[1]大神回答里的一个例子：

我们利用 f(x) = sin(x) 来求 π 的值，我们都知道在 [π/2, π] 区间内， sin(π) = 0，所以我们求 f(x) = 0 的解就可以间接求出π的值。

在这个问题下，迭代公式为：

我们以 x0 = 3 为迭代起始点，进行迭代，得到的结果如下：

x0=3.0(1位)x1=3.1411...(4位)x2=3.14159265357...(11位)x3=3.1415926535897932384626433832795020...(34位)x4=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706786...(102位)x5=3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412734...(301位)

可以看到，短短经过五次迭代，我们计算得到的圆周率已经超过了300位，每次迭代我们的精度都会提升三倍以上，这是非常令人震惊的。

无法收敛的情况

但令人遗憾的是并不是所有方程使用牛顿迭代法都可以有这么好的效果，对于一些方程，甚至可能会出现越走越偏的情况。我们再举个例子，比如方程:

如果我们画出它的迭代过程，是这样的：

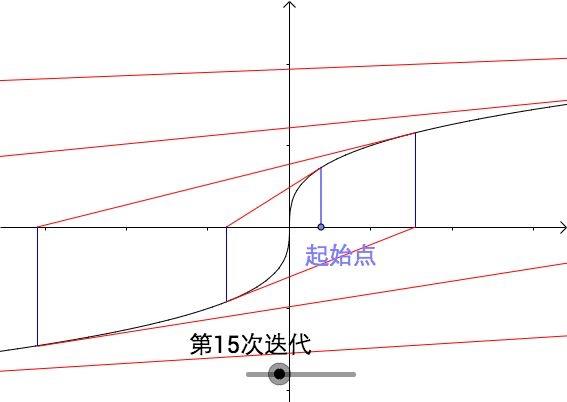
我们观察一下上面的迭代公式也可以看得出来，我们把 -1/f'(xn) 看成是系数，我们对 f(x) 求导算下这个系数，可以得到它的系数是3*x^{2/3}，观察一下就能发现随着x的增大，这个系数也是在增大的。也就是说，随着我们的迭代，这个值会变得越来越大，也就意味着我们的振幅越来越大，也就离收敛越来越远。

虽然少数情况下牛顿迭代法不能收敛，但是大多数情况下它效果都非常好。二分法固定每次缩短一半的区间，而牛顿迭代法的迭代效率往往更高，一般情况下使用牛顿迭代法可以获得更快的收敛速度。和二分法相比，牛顿迭代法的公式也并不难写，并且它在机器学习当中也有应用，学会它真的非常划算！

今天关于二分和牛顿迭代法的文章就到这里，如果觉得有所收获，请顺手点个关注或者转发吧，你们的举手之劳对我来说很重要。