学习Python中用numpy与matplotlib遇到的一些数学函数与函数的绘图

学习Python中的一些数学函数与函数的绘图

主要用到numpy 与 matplotlib
如果有什么不正确，欢迎指教。

图片不知道怎样批量上传，一个一个怎么感觉很小，请见谅

自行复制拷贝，到vs，jupyter notebook, spyder都可以

函数 y=x−sinxy = x - sinx y=x−sinx

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题x1 = np.linspace(-np.pi, np.pi, 1000)
y1 = x1 - np.sin(x1)plt.plot(x1, y1, c = 'k', label = r"$ y=x-sinx $")plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

函数 y=3x4−4x3+1y = 3x^4 - 4x^3 + 1 y=3x4−4x3+1

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题x1 = np.linspace(-1, 1.5, 1000)
y1 = 3 * (x1 ** 4) - 4 * (x1 ** 3) + 1
plt.plot(x1, y1, label = r"$ y = 3x^4 - 4x^3 + 1 $")plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

函数 y=x4y = x^4 y=x4

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题x1 = np.linspace(-5, 5, 1000)
y1 = x1 ** 4plt.plot(x1, y1, label = r"$ y = x^4 $")plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

函数 y=x3y = \sqrt[3]{x} y=3x​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题x1 = np.linspace(0, 5, 1000)
y1 = x1 ** (1/3)plt.plot(x1, y1, label = r"$ y = \sqrt[3]{x} $")# plt.xlim([-np.pi, np.pi])
# plt.ylim([-1.5, 1.5])
plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

函数 y=2x3−9x2+12x−3y=2x^3-9x^2+12x-3 y=2x3−9x2+12x−3

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题x1 = np.linspace(-2, 5, 1000)
y1 =2 * (x1 ** 3) - 9 * (x1 ** 2) + 12 * x1 - 3plt.plot(x1, y1, label = r"$ y=2x^3-9x^2+12x-3 $")plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

函数 y=2x3−6x2−18x+7y=2x^3-6x^2-18x+7 y=2x3−6x2−18x+7

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题x1 = np.linspace(-3, 5, 1000)
y1 = 2 * (x1 ** 3) - 6 * (x1 ** 2) - 18 * x1 + 7plt.plot(x1, y1, label = r"$ y=2x^3-6x^2-18x+7 $")# plt.axis('equal')
plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

三次抛物线 y=x3y = x^3 y=x3

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))x1 = np.linspace(-5, 5, 1000)
y1 = x1 ** 3plt.plot(x1, y1, label = r"$ y = x^3 $")plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

半立方抛物线 y2=ax3y^2 = ax^3 y2=ax3

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题a = 0.1
t = np.linspace(-5, 5, 1000)
x = t ** 2
y = a * (t ** 3)
plt.plot(x, y, label = r"y^2 = ax^3|a=0.1")a = 1
y1 = a * (t ** 3)
plt.plot(x, y1, label = r"y^2 = ax^3|a=1")# plt.xlim([-np.pi, np.pi])
# plt.ylim([-1.5, 1.5])
plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

概率曲线 y=e−x2y=e^{-x^2} y=e−x2

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题t = np.linspace(-2, 2, 1000)
x = t
y = np.e ** -(x ** 2)
plt.plot(x, y, label = r"$ y=e^{-x^2} $")plt.axis('equal')
# plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

箕舌线 y=8a3x2+4a2y =\frac{8a^3}{x^2+4a^2} y=x2+4a28a3​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题a = 1
t = np.linspace(-5, 5, 1000)
x = t
y = (8 * a ** 2) / (x ** 2 + 4 * a ** 2)
plt.plot(x, y, label = r"$ y =\frac{8a^3}{x^2+4a^2} |_{a=1} $")a = 2
y1 = (8 * a ** 2) / (x ** 2 + 4 * a ** 2)
plt.plot(x, y1, label = r"$ y =\frac{8a^3}{x^2+4a^2} |_{a=2} $")plt.axis('equal')
# plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

蔓叶线 y2(2a−x)=x3y^2(2a-x)=x^3 y2(2a−x)=x3 或 x=2asin2θ,y=2a2tan2θsin4θx=2asin^2\theta, y=2a^2tan^2\theta sin^4\theta x=2asin2θ,y=2a2tan2θsin4θ

修改：之前x的取值是−3.6≤x≤3.6-3.6\leq x \leq3.6−3.6≤x≤3.6, 实际上x的值是 ≥0\geq 0≥0

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题a = 2
#这是原来的取值范围
#t = np.linspace(-3.6, 3.6, 1000)
#x = np.abs(t)
#这是现在的取值范围
t = np.linspace(0, 3.6, 1000)
x = t
#还有我用power替代了sqrt开根号
y = np.power((x ** 3) / (2 * a - x), 1/2)
plt.plot(x, y, 'b', x, -y, 'b', label = r"$ y^2(2a-x)=x^3 $")plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

ρ=2a−tan2θ\rho=2a-tan^2\theta ρ=2a−tan2θ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
plt.ylim([0, 6])a = 1
theta = np.arange(0, 2 * np.pi, np.pi / 100)
rho = 2 * a - np.tan(theta) ** 2
plt.plot(theta, rho, label = r'$\rho=2a-tan^2\theta \quad |a=1$')a = 1.5
r2 = a * rho
plt.plot(theta, r2, label = r'$\rho=2a-tan^2\theta \quad |a=1.5$')a = 2.5
r2 = a * rho
plt.plot(theta, r2, label = r'$\rho=2a-tan^2\theta \quad |a=2.5$')plt.legend()
plt.show()

在这里插入图片描述

笛卡儿叶形线画图 极坐标 r=3asinθcosθsin3θ+cos3θr = \frac{3asin\theta cos\theta}{sin^3\theta + cos^3\theta} r=sin3θ+cos3θ3asinθcosθ​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
plt.ylim([0, 6])a = 1
theta = np.arange(0, 2 * np.pi, np.pi / 100)
r = 3 * a * np.sin(theta) * np.cos(theta) / (np.sin(theta) ** 3 + np.cos(theta) ** 3)
plt.plot(theta, r, label = r'$ r = \frac{3asin\theta cos\theta}{sin^3\theta + cos^3\theta} $')a = 1.5
r2 = a * r
plt.plot(theta, r2)a = 2.5
r2 = a * r
plt.plot(theta, r2)# plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

笛卡儿叶形线 直角坐标 x3+y3−3axy=0x^3+y^3-3axy=0 x3+y3−3axy=0 或 x=3at1+t3,y=3at21+t3x=\frac{3at}{1+t^3}, y=\frac{3at^2}{1+t^3} x=1+t33at​,y=1+t33at2​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
# plt.subplot(111, polar = True)
# plt.ylim([0, 6])a = 1
# t = np.arange(-0.1, 4 * np.pi, np.pi / 180)
t = np.linspace(-0.5, 200, 5000)
x = (3 * a * t) / (1 + t ** 3)
y = (3 * a * t ** 2) / (1 + t ** 3)
plt.plot(x, y, label = r'$ x=\frac{3at}{1+t^3}, y=\frac{3at^2}{1+t^3} $')a = 1.5
x1 = (3 * a * t) / (1 + t ** 3)
y1 = (3 * a * t ** 2) / (1 + t ** 3)
plt.plot(x1, y1, label = r'$ x=\frac{3at}{1+t^3}, y=\frac{3at^2}{1+t^3} $')# plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

星形线（内摆线的一种） x23+y23=a23x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3} x32​+y32​=a32​ 或 {x=acos3θy=asin3θ\begin{cases} x=acos^3\theta \\ y=asin^3\theta \end{cases} {x=acos3θy=asin3θ​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题a = 1
theta = np.arange(0, 2 * np.pi, np.pi / 180)
x = a * np.cos(theta) ** 3
y = a * np.sin(theta) ** 3
plt.plot(x, y, label = r'$ x=acos^3\theta, y=asin^3\theta \quad|a=1$')a = 2
x1 = a * x
y1 = a * y
plt.plot(x1, y1, label = r'$ x=acos^3\theta, y=asin^3\theta \quad|a=2$')a = 3
x2 = a * x
y2 = a * y
plt.plot(x2, y2, label = r'$ x=acos^3\theta, y=asin^3\theta \quad|a=3$')ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))plt.axis('equal')
plt.legend()
plt.show()

在这里插入图片描述

摆线 {x=a(θ−sinθ)y=a(1−cosθ)\begin{cases} x=a(\theta-sin\theta) \\ y=a(1-cos\theta) \end{cases} {x=a(θ−sinθ)y=a(1−cosθ)​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
# plt.subplot(111, polar = True)
# plt.ylim([0, 6])a = 1
theta = np.arange(0, 4 * np.pi, np.pi / 180)
x = a * (theta - np.sin(theta))
y = a * (1 - np.cos(theta))
plt.plot(x, y, label = r'$ x=a(\theta-sin\theta),\quad y=a(1-cos\theta) \quad|a=1$')a = 2
x1 = a * x
y1 = a * y
plt.plot(x1, y1, label = r'$ x=a(\theta-sin\theta),\quad y=a(1-cos\theta) \quad|a=2$')a = 3
x2 = a * x
y2 = a * y
plt.plot(x2, y2, label = r'$ x=a(\theta-sin\theta),\quad y=a(1-cos\theta) \quad|a=3$')ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))plt.axis('equal')
plt.legend()
plt.show()

在这里插入图片描述

心形线（外摆线的一种） KaTeX parse error: Can't use function '$' in math mode at position 27: …a\sqrt{x^2+y^2}$̲ 或 $ \rho=a(1-c…

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
# plt.ylim([0, 6])a = 1
theta = np.arange(0, 2 * np.pi, np.pi / 180)
y = a * (1 - np.cos(theta))
plt.plot(theta, y, label = r'$ \rho=a(1-cos\theta) $')y1 = a * (1 - np.sin(theta))
plt.plot(theta, y1, label = r'$ \rho=a(1-sin\theta) $')# a = 2
# x1 = a * x
# y1 = a * y
# plt.plot(x1, y1, label = r'$ x=a(\theta-sin\theta),\quad y=a(1-cos\theta) \quad|a=2$')# a = 3
# x2 = a * x
# y2 = a * y
# plt.plot(x2, y2, label = r'$ x=a(\theta-sin\theta),\quad y=a(1-cos\theta) \quad|a=3$')# ax = plt.gca()
# ax.spines['right'].set_color('none')
# ax.spines['top'].set_color('none')
# ax.xaxis.set_ticks_position('bottom')
# ax.spines['bottom'].set_position(('data', 0))
# ax.yaxis.set_ticks_position('left')
# ax.spines['left'].set_position(('data', 0))# plt.axis('equal')
plt.legend()
plt.show()

在这里插入图片描述

x=sinθ,y=cosθ+x23x=sin\theta,\quad y=cos\theta+\sqrt[3]{x^2}x=sinθ,y=cosθ+3x2​

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题a = 1
theta = np.arange(0, 2 * np.pi, np.pi / 180)
x = np.sin(theta)
y = np.cos(theta) + np.power((x ** 2), 1 / 3)  #原来用 y = np.cos(theta) + np.power(x, 2/3)只画出一半，而且报power的错
plt.plot(x, y, label = r'$x=sin\theta,\quady=cos\theta+\sqrt[3]{x^2}$')# ax = plt.gca()
# ax.spines['right'].set_color('none')
# ax.spines['top'].set_color('none')
# ax.xaxis.set_ticks_position('bottom')
# ax.spines['bottom'].set_position(('data', 0))
# ax.yaxis.set_ticks_position('left')
# ax.spines['left'].set_position(('data', 0))plt.axis('equal') #等比例会好看点
plt.legend()
plt.show()

在这里插入图片描述

阿基米德螺线 ρ=aθ\rho=a\thetaρ=aθ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
# plt.ylim([0, 6])a = 1
theta = np.arange(0, 4 * np.pi, np.pi / 180)
rho = a * theta
plt.plot(theta, rho, label = r'$\rho=a\theta$', linestyle = 'solid')# rho1 = - a * theta
# plt.plot(theta, rho1, label = r'$\rho=a\theta$')plt.legend()
plt.show()

在这里插入图片描述

对数螺线 ρ=eaθ\rho=e^{a\theta} ρ=eaθ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
plt.ylim([0, 10])a = 0.1
theta = np.arange(0, 6 * np.pi, np.pi / 180)
rho = np.e ** (a * theta)
plt.plot(theta, rho, label = r'$ \rho=e^{a\theta} $', linestyle = 'solid')a = 0.2
rho1 = np.e ** (a * theta)
plt.plot(theta, rho1, label = r'$ \rho=e^{a\theta} $', linestyle = 'solid')plt.legend()
plt.show()

在这里插入图片描述

双曲螺旋线 ρθ=a\rho\theta=a ρθ=a

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
plt.ylim([0, 30])a = 30
theta = np.arange(0.01, 6 * np.pi, np.pi / 180)
rho = a / theta
plt.plot(theta, rho, label = r'$ \rho\theta=a \quad |a=30 $', linestyle = 'solid')a = 50
rho1 = a / theta
plt.plot(theta, rho1, label = r'$ \rho\theta=a \quad |a=50 $', linestyle = 'solid')plt.legend()
plt.show()

在这里插入图片描述

伯努利双纽线 (x2+y2)2=2a2xy(x^2+y^2)^2=2a^2xy(x2+y2)2=2a2xy 或 (x2+y2)2=a2(x2−y2)(x^2+y^2)^2=a^2(x^2-y^2)(x2+y2)2=a2(x2−y2) 或 ρ2=a2sin2θ\rho^2=a^2sin2\theta ρ2=a2sin2θ 或 ρ2=a2cos2θ\rho^2=a^2cos2\thetaρ2=a2cos2θ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
# plt.subplot(111, polar = True)
# plt.ylim([0, 30])a = 1
theta = np.linspace(-np.pi, np.pi, 200)
x = a * np.sqrt(2) * np.cos(theta) / (np.sin(theta) ** 2 + 1)
y = a * np.sqrt(2) * np.cos(theta) * np.sin(theta) / (np.sin(theta) ** 2 + 1)
plt.plot(x, y, label = r'$ \rho^2=a^2cos2\theta \quad |a=1 $', linestyle = 'solid')plt.axis('equal')
plt.legend()
plt.show()

在这里插入图片描述

三叶玫瑰线 ρ=acos3θ\rho=acos3\thetaρ=acos3θ 或 ρ=asin3θ\rho=asin3\theta ρ=asin3θ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# plt.rcParams['figure.figsize'] = (8, 4.5)
# plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
# plt.ylim([0, 30])a = 1
theta = np.linspace(0, 2 * np.pi, 200)
rho = a * np.cos(3 * theta)
plt.plot(theta, rho, label = r'$ \rho=acos3\theta \quad |a=1 $', linestyle = 'solid')# a = 2
# rho1 = a * rho
# plt.plot(theta, rho1, label = r'$ \rho=acos3\theta \quad |a=2 $', linestyle = 'solid')a = 1
rho2 = a * np.sin(3 * theta)
plt.plot(theta, rho2, label = r'$ \rho=asin3\theta \quad |a=1 $', linestyle = 'solid')plt.legend()
plt.show()

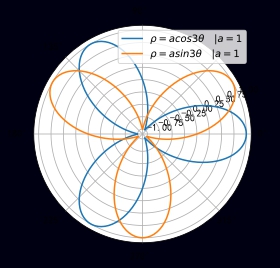
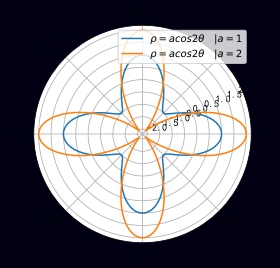
在这里插入图片描述

四叶玫瑰线 ρ=acos2θ\rho=acos2\theta ρ=acos2θ 或 ρ=asin2θ\rho=asin2\theta ρ=asin2θ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# plt.rcParams['figure.figsize'] = (8, 4.5)
# plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
# plt.ylim([0, 30])a = 1
theta = np.linspace(0, 2 * np.pi, 200)
rho = a * np.cos(4 * theta)
plt.plot(theta, rho, label = r'$ \rho=acos2\theta \quad |a=1 $', linestyle = 'solid')a = 2
rho1 = a * rho
plt.plot(theta, rho1, label = r'$ \rho=acos2\theta \quad |a=2 $', linestyle = 'solid')# a = 1
# rho2 = a * np.sin(4 * theta)
# plt.plot(theta, rho2, label = r'$ \rho=asin2\theta \quad |a=1 $', linestyle = 'solid')plt.legend()
plt.show()

在这里插入图片描述

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# plt.rcParams['figure.figsize'] = (8, 4.5)
# plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
# plt.ylim([0, 30])theta = np.linspace(0, 2 * np.pi, 200)a = 1
rho = a * np.sin(4 * theta)
plt.plot(theta, rho, label = r'$ \rho=asin2\theta \quad |a=1 $', linestyle = 'solid')a = 2
rho1 = a * np.sin(4 * theta)
plt.plot(theta, rho1, label = r'$ \rho=asin2\theta \quad |a=2 $', linestyle = '--')plt.legend()
plt.show()

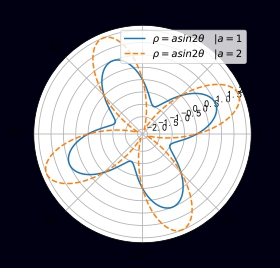
在这里插入图片描述

多叶玫瑰线 ρ=acosnθ\rho=acosn\theta ρ=acosnθ 或 ρ=asinnθ,∣n=1,2,3...\rho=asinn\theta,\quad|n=1,2,3...ρ=asinnθ,∣n=1,2,3...

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# plt.rcParams['figure.figsize'] = (8, 4.5)
# plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
plt.subplot(111, polar = True)
# plt.ylim([0, 30])theta = np.linspace(0, 2 * np.pi, 200)a = 1
n = 20
rho = a * np.sin(10 * theta)
plt.plot(theta, rho, label = r'$ \rho=asinn\theta \quad |a=1,n=10 $', linestyle = 'solid')plt.legend()
plt.show()

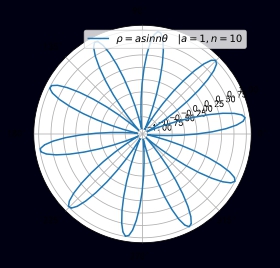
在这里插入图片描述

函数 四叶线 x=aρsinθ,y=aρcosθ,ρ=2sinsin2θx=a\rho sin\theta,y=a\rho cos\theta, \rho = \sqrt{2}sin{sin2\theta}x=aρsinθ,y=aρcosθ,ρ=2​sinsin2θ

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
# plt.subplot(111, polar = True)
# plt.ylim([0, 30])a = 1
theta = np.linspace(-np.pi, np.pi, 200)
rho = np.sqrt(2) * np.sin(np.sin(2*theta))
x = a * rho * np.sin(theta)
y = a * rho * np.cos(theta)
plt.plot(x, y, label = r'$x=a\rho sin\theta,y=a\rho cos\theta, \rho = \sqrt{2}sin{sin2\theta}$', linestyle = 'solid')plt.axis('equal')
plt.legend()
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vELrwNwd-1589013522141)(output_52_0.svg)]在这里插入图片描述

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['figure.figsize'] = (8, 4.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
# plt.subplot(111, polar = True)
# plt.ylim([0, 30])a = 1
theta = np.linspace(-np.pi, np.pi, 200)
rho = np.sqrt(2) * np.sin(np.sin(4*theta))
x = a * rho * np.sin(theta)
y = a * rho * np.cos(theta)
plt.plot(x, y, label = r'$x=a\rho sin\theta,y=a\rho cos\theta, \rho = \sqrt{2}sin{sin2\theta}$', linestyle = 'solid')plt.axis('equal')
plt.legend()
plt.show()

在这里插入图片描述

函数 四叶线 x=aρsinθ,y=aρcosθ,ρ=2sin∣sin2θ∣x=a\rho sin\theta,y=a\rho cos\theta, \rho = \sqrt{2}sin{\vert sin2\theta \vert}x=aρsinθ,y=aρcosθ,ρ=2​sin∣sin2θ∣

%matplotlib inline
%config InlineBackend.figure_format = "svg"
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# plt.rcParams['figure.figsize'] = (8, 4.5)
# plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['Simhei']  #替代字体
plt.rcParams['axes.unicode_minus'] = False  #解决坐标轴负数的铅显示问题#极坐标
# plt.subplot(111, polar = True)
# plt.ylim([0, 30])a = 1
theta = np.linspace(-np.pi, np.pi, 1000)
rho = np.sqrt(2) * np.sqrt(abs(np.sin(10*theta)) + 0.5)
x = a * rho * np.sin(theta)
y = a * rho * np.cos(theta)
plt.plot(x, y,  linestyle = 'solid')# label = r'$x=a\rho sin\theta,y=a\rho cos\theta, \rho = \sqrt{2}sin{sin2\theta}$',plt.axis('equal')
# plt.legend()
plt.show()

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/260906.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

有这个OCR程序，不用再买VIP了，Python 调用百度OCR API

有这个OCR程序，不用再买VIP了，Python 调用百度OCR API

最近学习，很多东西都是视频，截图后，又想做成文档保存起来。 刚开始不多，打一下字就很快解决了。 随着时间的推移，现在越来越多的图了，管理起来确实不方便，打字有时也不能很快的解决。 所以就…
阅读更多...
linux常用命令_Linux常用命令全称

linux常用命令_Linux常用命令全称

从事IT行业的很多人都会使用Linux常用命令，但是知道这些常用命令全称的人并不多，让我们来看看这些常用命令对应的全称吧！必备Linux命令和C语言基础_C语言_嵌入式开发工程师-创客学院​www.makeru.com.cnpwd:print work directory 打印当前目录…
阅读更多...
存储程序(1)——MYSQL

存储程序(1)——MYSQL

MySQL支持把几种对象存放在服务器端供以后使用。这几种对象有一些可以根据情况通过程序代码调用，有一些会在数据表被修改时自动执行，还有一些可以在预定时刻自动执行。它们包括以下几种: 1.存储函数(stored function)。返回一个计算结果，该结…
阅读更多...
闯过这 54 关，点亮你的 Git 技能树 (五) - 完结篇

闯过这 54 关，点亮你的 Git 技能树 (五) - 完结篇

这是一个系列文章，介绍学习 Git 的一个小游戏 - githug，如果你是第一次看到，请先阅读：闯过这 54 关，点亮你的 Git 技能树闯过这 54 关，点亮你的 Git 技能树（一）闯过这 54 关&#xf…
阅读更多...
Jupyter notebook 不安装主题，通过修改css更改 默认字体，字体大小等

Jupyter notebook 不安装主题，通过修改css更改 默认字体，字体大小等

目标： Jupyter notebook 又不想改更主题的的情况下，可以通过修改css的目的来达到修改默认的字体，字号心达到可以好的阅读效果。 方法 要修改的css文件目录如下， D:\Anaconda\Lib\site-packages\notebook\static\custom 这个就是…
阅读更多...
坚果nuts 加速 官网_【喂你播】坚果手机2020新品发布会来了；三星定向华为手机推以旧换新...

坚果nuts 加速 官网_【喂你播】坚果手机2020新品发布会来了；三星定向华为手机推以旧换新...

周五喂diu 不只有你们爱的女主播 还有小编呢BGM：Make You Hustle-Croatia Squad坚果手机2020新品发布会来了坚果手机正式宣布：坚果手机2020新品发布会将于10月20日19:30在五棵松M空间举行。根据此前爆料，坚果手机新品或命名为坚果Pro4&#x…
阅读更多...
图像处理核函数：之高斯核的生成方法 python

图像处理核函数：之高斯核的生成方法 python

图像处理核函数：之高斯核函数的生成方法 python高斯核函数（低通高斯滤波器核）高斯分布函数高斯核生成函数代码效果高斯核函数的图像高斯核函数（低通高斯滤波器核） 最近在看DIP（Digital Image Processing)&…
阅读更多...
WEB-INFO/lib build path 的jar包问题

WEB-INFO/lib build path 的jar包问题

为什么80%的码农都做不了架构师？>>> 一、build path&WEB-INFO/lib介绍 build path：可以说是引用； WEB-INFO/lib：可以说是固定在一个地方； eclipse编译项目的时候是根据build path的，如果…
阅读更多...
Windows phone 7之页面布局

Windows phone 7之页面布局

Windows phone的页面布局方式一般是依赖布局控件实现的，而布局控件有三种Grid，StackPanel和Canvas Grid是网格布局方式，相当于一个表格，有行和列，新建一个Windows phone项目，打开MainPage.xaml，…
阅读更多...
苹果电脑删除软件_软件自动开启很烦人？如何彻底关掉开机自动开启的应用程序...

苹果电脑删除软件_软件自动开启很烦人？如何彻底关掉开机自动开启的应用程序...

使用Mac的小伙伴有没有这样的烦恼，电脑一开机，一堆烦人的软件就自动开启了，让人很懊恼，如何才能彻底关掉开机自动开启的应用程序？mac开机启动项怎么设置？开机启动项要怎么禁止？今天就带大家解决…
阅读更多...
csgo怎么控制电脑玩家_电脑远程控制怎么弄

csgo怎么控制电脑玩家_电脑远程控制怎么弄

本教程以“Win 10”系统为例进行演示。方法一：1/6在“此电脑”单击鼠标右键选择“属性”2/6在弹出窗口中点击“远程设置”3/6勾选“允许远程协助连接这台计算机”，然后点击应用并确定4/6在微软小娜搜索“mstsc”5/6打开“远程桌面连接”6/6输入对方的IP地…
阅读更多...
MNIST 手写数字识别，我是如何做到886个可训练参数，识别率达到98.2%? (参数、模型压缩）， Keras实现，模型优化

MNIST 手写数字识别，我是如何做到886个可训练参数，识别率达到98.2%? (参数、模型压缩）， Keras实现，模型优化

一 项目展示 下面可以看到验证集可以到了0.9823了，实际上，在下面的另外一个训练，可以得到0.9839，我保守的写了0.982 二 项目参数展示 我们先来看看LeNet 5 的结构与参数，参数有61，706个。 这个是我用…
阅读更多...
javascript 计算两个坐标的距离 米_土方全面应用计算

javascript 计算两个坐标的距离 米_土方全面应用计算

各种土方量的计算方法汇总8.2.1 DTM法土方计算由DTM模型来计算土方量是根据实地测定的地面点坐标(X，Y，Z)和设计高程，通过生成三角网来计算每一个三棱锥的填挖方量，最后累计得到指定范围内填方和挖方的土方量，并绘出填…
阅读更多...
unity 阳光插件_网络广告，阳光创信保驾护航

unity 阳光插件_网络广告，阳光创信保驾护航

网络广告 就找阳光创信。网络营销的技术基础主要是以计算机网络技术为代表的信息技术。计算机网络是现代通信技术与计算机技术相结合的产物，它把分布在不同地理区域的计算机与专门的外部设备用通信线路互连成一个规模大、功能强的网络，从而使众多的计算机…
阅读更多...
第2章 Python 数字图像处理(DIP) --数字图像基础1 - 视觉感知要素 - 亮度适应与辨别

第2章 Python 数字图像处理(DIP) --数字图像基础1 - 视觉感知要素 - 亮度适应与辨别

数字图像基础1视觉感知要素亮度适应与辨别import sys import numpy as np import cv2 import matplotlib import matplotlib.pyplot as plt import PIL from PIL import Imageprint(f"Python version: {sys.version}") print(f"Numpy version: {np.__version__…
阅读更多...
快速幂与快速乘法

快速幂与快速乘法

List 快速幂与快速乘法 ListKnowledge快速幂 原理code快速乘法 原理codeKnowledge 快速幂 原理 a^b%p 采用二进制得思想，将b转化为二进制数。 b c02^0c12^1c22^2c32^3……cn2^n a^b a^(a12^0)a^(c12^1)……a^(cn2^n) 所以我们可以在log(b)的时间内求出a^(2^0)…
阅读更多...
Java程序设计 图形用户界面 小巫版简易计算器

Java程序设计 图形用户界面 小巫版简易计算器

/** 作者：wwj 时间：2012/4/13 功能：实现一个计算器应用程序实验要求：编写一个模拟计算器的应用程序，使用面板和网格布局， 添加一个文本框，10个数字按钮（0~9），…
阅读更多...
phython在file同时写入两个_轻松支撑百万级数据点写入 京东智联云时序数据库HoraeDB架构解密...

phython在file同时写入两个_轻松支撑百万级数据点写入 京东智联云时序数据库HoraeDB架构解密...

本文将通过对时序数据的基本概念、应用场景以及京东智联云时序数据库HoraeDB的介绍，为大家揭秘HoraeDB的核心技术架构和解决方案。首先我们来了解下时序数据库的基本概念。时序数据库全称时间序列数据库，主要用于处理带时间标签的数据，带时间…
阅读更多...
飞雪迎春

飞雪迎春

转载于:https://www.cnblogs.com/ysx4221/p/3537810.html
阅读更多...
高可用集群技术之corosync应用详解(一)

高可用集群技术之corosync应用详解(一)

Corosync概述:Corosync是集群管理套件的一部分，它在传递信息的时候可以通过一个简单的配置文件来定义信息传递的方式和协议等。它是一个新兴的软件，2008年推出，但其实它并不是一个真正意义上的新软件，在2002年的时候有一个项目Ope…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023