1 二阶控制系统模型本文引用地址：http://www.eepw.com.cn/article/201612/328597.htm

能够用二阶微分方程描述的系统称为二阶控制系统。在控制工程实践中，二阶控制系统十分常见，例如，电枢控制的直流电动机，RLC网络和弹簧-质量-阻尼器组成的机械位移系统等。此外，许多高阶系统在一定条件下，常常近似地作为二阶控制系统来研究。因此，详细讨论和分析二阶控制系统的特性，具有极为重要的实际意义。典型二阶控制系统数学模型结构如图1所示。

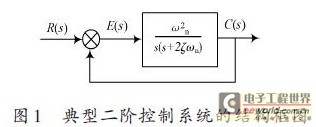
其闭环传递函数为：

式中：ζ为系统阻尼比;ωn为无阻尼自然振荡角频率，单位为rad/s.二阶控制系统的动态特性可由以上两个参数描述。二阶控制系统在单位阶跃信号作用下，其输出响应可分为以下几种情况：

(1)当ζ=0时，二阶控制系统为零阻尼状态。系统有一对共轭虚根，系统单位阶跃响应为无阻尼等幅振荡曲线。

(2)当0

(3)当ζ=1时，二阶控制系统为临界阻尼状态。系统具有两个相同的实数极点，位于S 左半平面。系统单位阶跃响应为无超调，无振荡单调上升的曲线，不存在稳态误差。

(4)当ζ>1时，二阶控制系统为过阻尼状态。系统具有两个不等的实数极点，位于S左半平面，系统单位阶跃响应与临界阻尼情况相似，为无超调，无振荡单调上升的曲线，但它的过渡过程时间较之临界阻尼更长。

2 二阶控制系统仿真设计与研究

2.1 二阶控制系统仿真结构设计

启动Matlab 7.04,进入Simulink仿真界面，根据二阶控制系统数学模型结构，设计二阶控制系统的Simu-link仿真结构如图2所示。双击各函数模块，在出现的各参数对话框内设置相应的参数，仿真时输入单位阶跃信号，起始时间为0,分别改变ωn 和ζ的值，点击simula-tion菜单下的start命令进行仿真，双击示波器模块观察仿真结果，得到系统的阶跃响应曲线，再进行分析ωn和ζ对系统动态性能的影响。

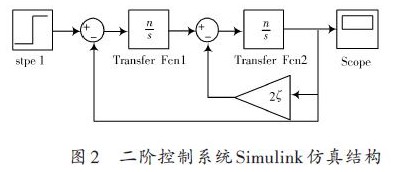2.2 二阶控制系统单位阶跃响应与参数ζ的关系

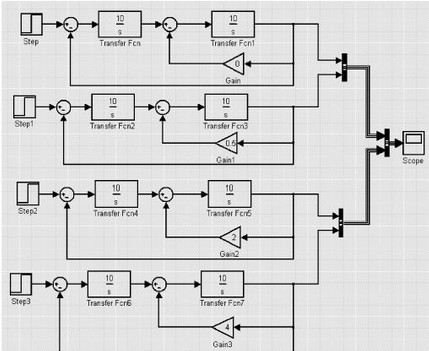
设定ωn=10 rad/s 不变，改变参数ζ分别为0,0.25,1和2的二阶控制系统Simulink仿真结构如图3所示，输入单位阶跃信号，其仿真响应曲线如图4所示。从图中实验数据分析可以看出，响应曲线由上至下，依次为无阻尼等幅振荡曲线，欠阻尼振荡衰减曲线，临界阻尼和过阻尼无超调单调上升曲线。当0

2.3 二阶控制系统单位阶跃响应与参数ωn的关系

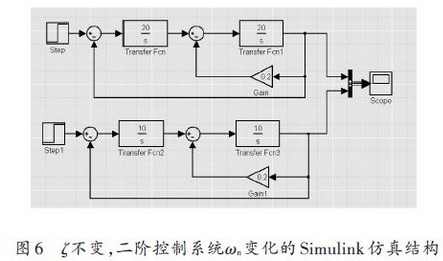
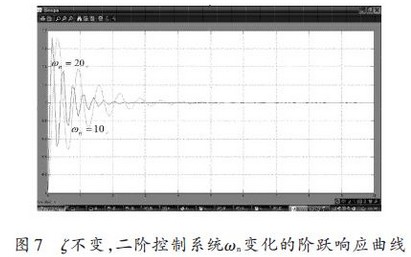
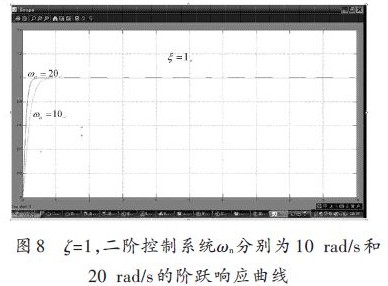
设定ζ=0.1 不变，改变参数ωn 分别为10 rad/s 和20 rad/s的二阶控制系统Simulink仿真结构如图6所示，输入单位阶跃信号，其仿真响应曲线如图7所示。从图中实验数据分析可以看出，当ζ=0.1 时，随着ωn 的增大，系统单位响应的振荡周期变短，其调整时间也相应地缩短;当ζ≥1 时，系统变成临界阻尼或欠阻尼系统，这时也有类似的结论，图8所示为当ζ=1时，ωn分别为10 rad/s和20 rad/s的二阶控制系统的阶跃响应曲线。

3 结语

基于Matlab/Simulink 环境的仿真分析方法，通过Simulink工具箱所提供的基本模块，不需任何硬件，在单位阶跃信号作用，利用仿真实例很好地实现了对二阶控制系统进行仿真研究，直接观察和分析二阶控制系统输出性能的变化，验证了二阶控制系统相关理论的正确性，在二阶控制系统实验教学和科研上有很大实用价值，充分体现了Matlab/Simulink仿真直观和方便的特点。