目录
索引(INDEX)基本概念
索引结构分类
B+Tree树索引结构
Hash索引结构
Full-Text索引
R-Tree索引
索引(INDEX)基本概念
什么是索引
索引是帮助MySQL高效获取数据的有序数据结构
为数据库表中的某些列创建索引,就是对数据库表中某些列的值通过不同的数据结构进行排序
为列建立索引之后,数据库除了维护数据之外,还会维护满足特定查找算法的数据结构,这些数据结构以某种方式指向数据,这样就可以在这些数据结构上实现快速查询,这种数据结构就是索引
索引的作用
通过索引可以将无序的数据变为有序的数据,能够实现快速访问数据库表中的特定信息
优缺点
优点
提高数据检索的效率,降低数据库的IO成本
通过索引对数据进行排序,降低数据排序的成本,降低CPU的消耗
缺点
索引会占用空间
索引提高了表的查询效率,但是却降低了更新表的速度(Insert、Update、Delete)
索引只是一个提高效率的因素,如果MySQL有大数据量的表,就需要花时间研究最优秀的索引(即需要研究为哪些字段建立索引能够使得效率提升到最大化,因为一条查询语句只会引用到一种索引,并且一般建议一个表建立的索引数量不要超过5个)
索引结构分类
索引结构主要分为四大类
B+Tree索引-(B+树)
最常见的索引类型,大部分的存储引擎都支持此索引
Hash索引-(Hash表)
底层的数据结构是用哈希表实现的,只有精确匹配索引列的查询才有效,不支持范围查询
Full-Text索引-(倒排索引)
又名全文索引,是一种通过建立倒排索引,快速匹配文档的方式
R-Tree索引(R-Tree树)
又名空间索引,是MyISAM引擎的一个特殊索引类型,主要用于地理位置数据,使用较少
存储引擎对不同索引的支持情况(默认B+Tree索引)
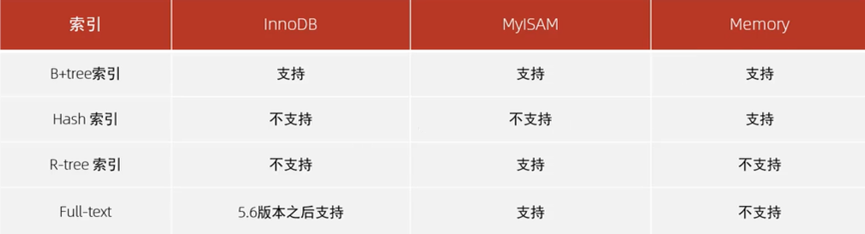
在MySQL数据库中,支持Hash索引的是Memory引擎;而InnoDB中具有自适应Hash的功能,根据B+tree索引在指定条件下自动构建的
B+Tree树索引结构
B+Tree树是由二叉树 → 红黑树(自平衡二叉树) → B-Tree树烟花而来的,我们在介绍B+Tree树之前先介绍这三种数据结构
二叉树
二叉树的每个节点最多有两个子节点(两颗子树);并且两个子节点是有序的
以单个节点为例:左边子节点是比自身小的,右边子节点是比自身大的
缺点
- 大数据量的情况下,层级较深,检索速度慢
- 容易形成倾斜树(左倾斜或右倾斜)
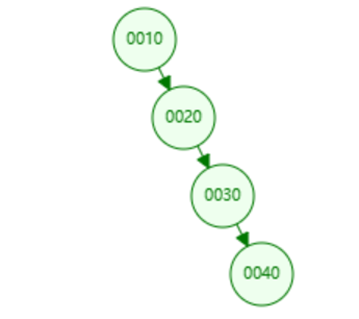
二叉树的工作原理
二叉树的数据插入(依次插入30、40、20、19、21、39、35)

二叉树的数据遍历

二叉树的数据查找(查找39 、21、25)
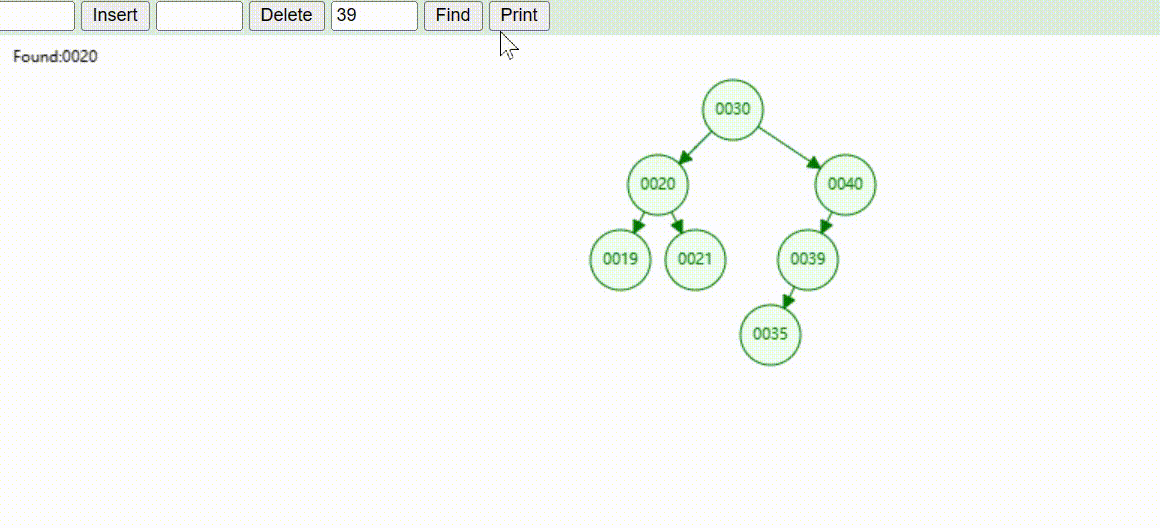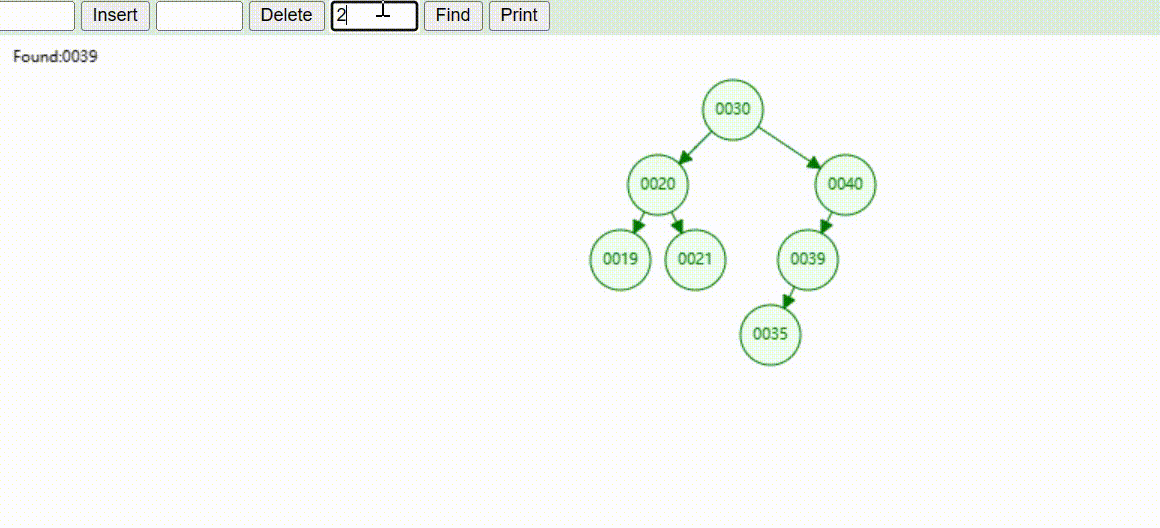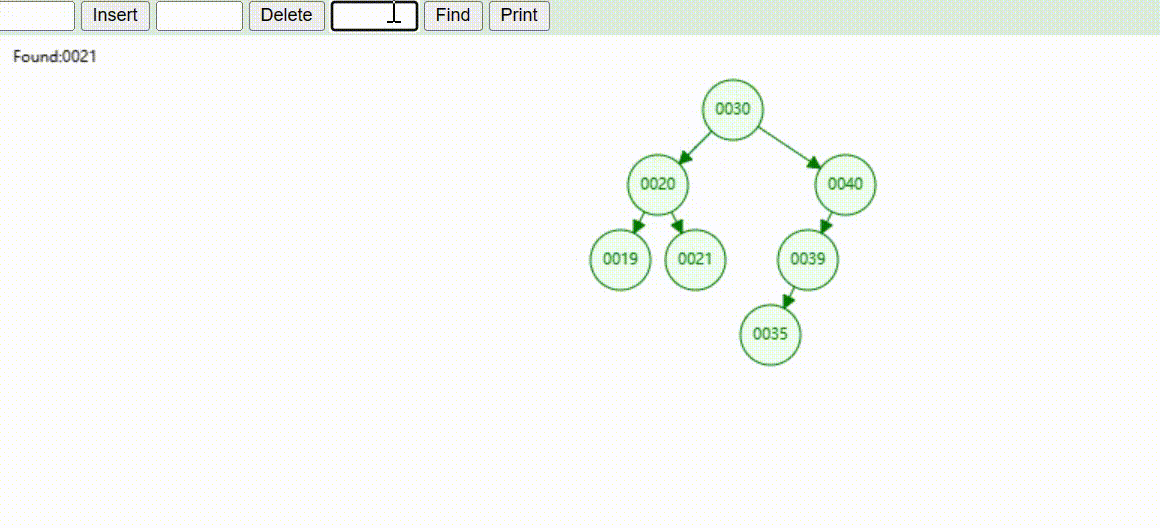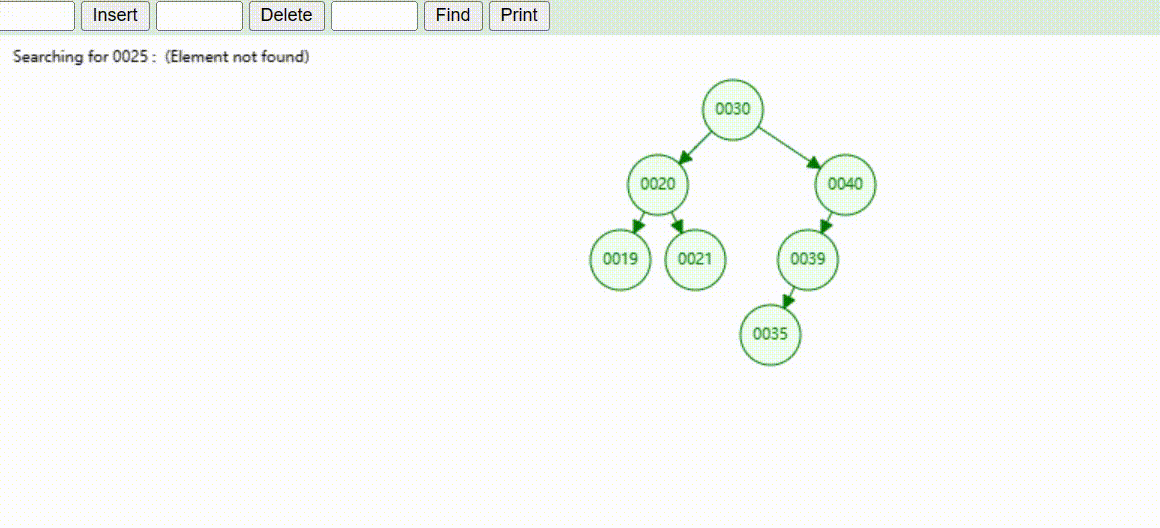
二叉树的数据删除(依次删除19、39、30)
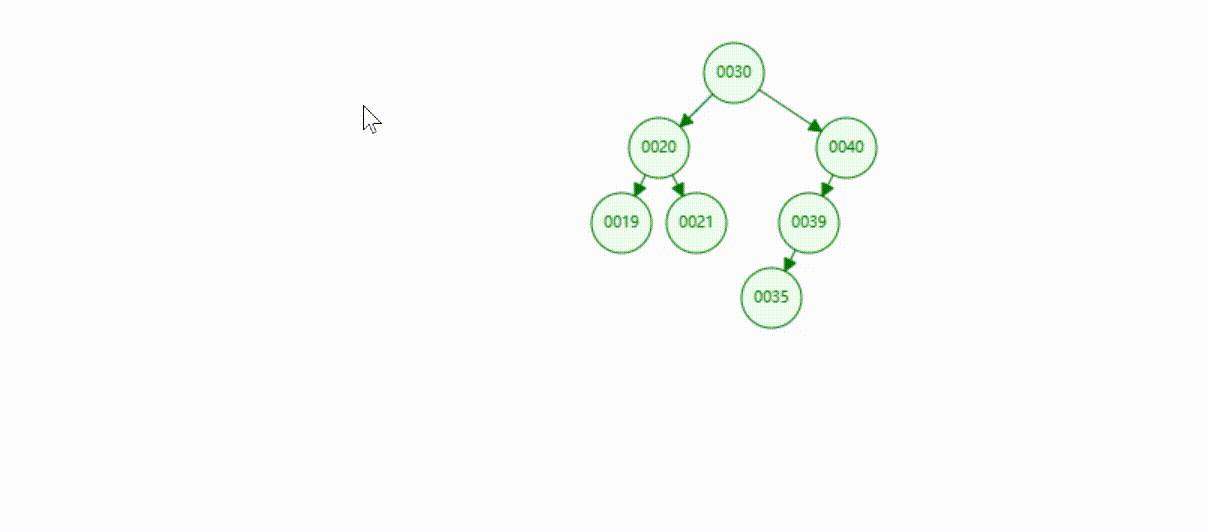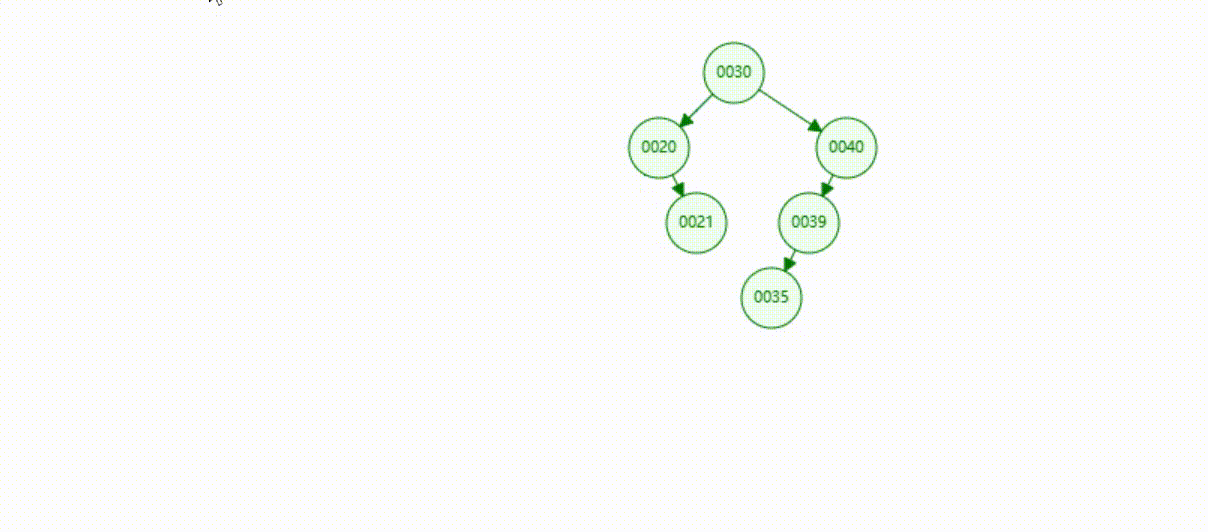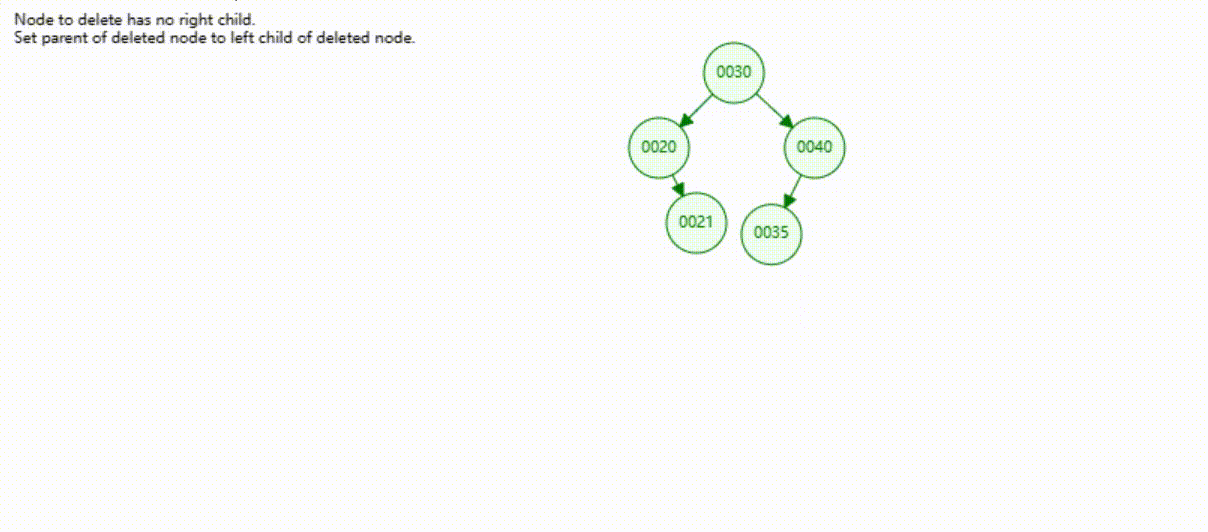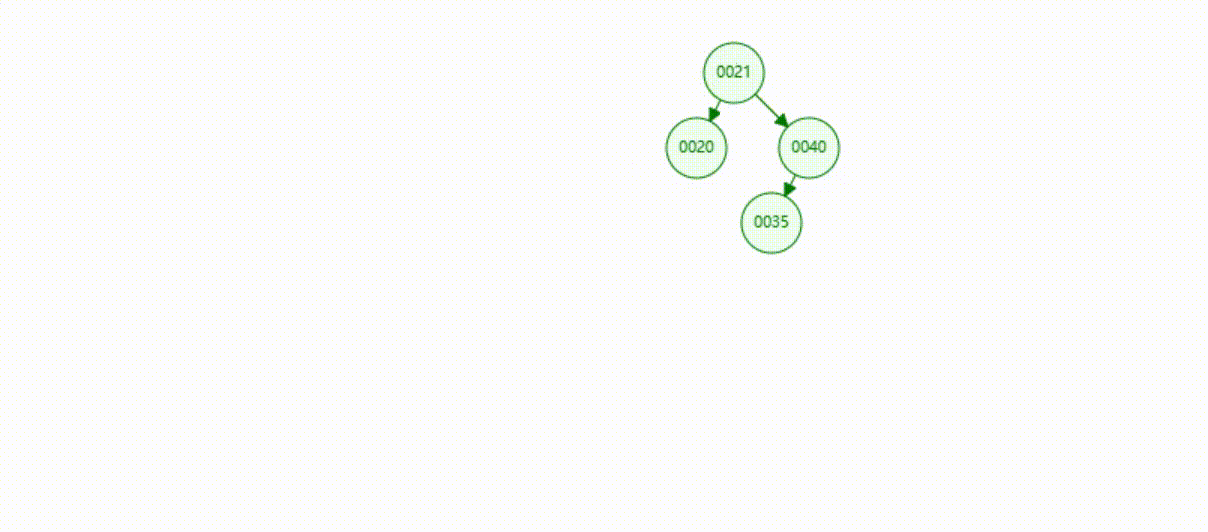
红黑树(自平衡二叉树)
红黑树时二叉树的变种,可以解决二叉树插入数值时产生斜树的问题
任何一个节点都有颜色(红色或黑色),通过颜色来确保树在插入和删除时的平衡
根节点一定是黑色的;Null节点被认为是黑色的;每个红色节点的两个叶子节点都是黑色
每个叶子节点到根的路径上不能出现连续的红色节点
任何一个节点到达叶子节点所经过的黑节点个数必须相等
当在红黑树中进行插入和删除操作时,会通过左旋、右旋、重新着色来修复树结构,保持树的平衡
缺点
- 在进行大量插入和删除操作的情况下,可能会造成频繁的树重构,影响性能
- 红黑树的实现比较复杂,需要维护节点的颜色和平衡
- 红黑树本质也是二叉树,在大数据量的情况下,层级较深,检索速度会下降
红黑树的工作原理
红黑树的数据插入(依次插入30、40、20、19、21、39、35) 使用到了右旋

红黑树的数据遍历
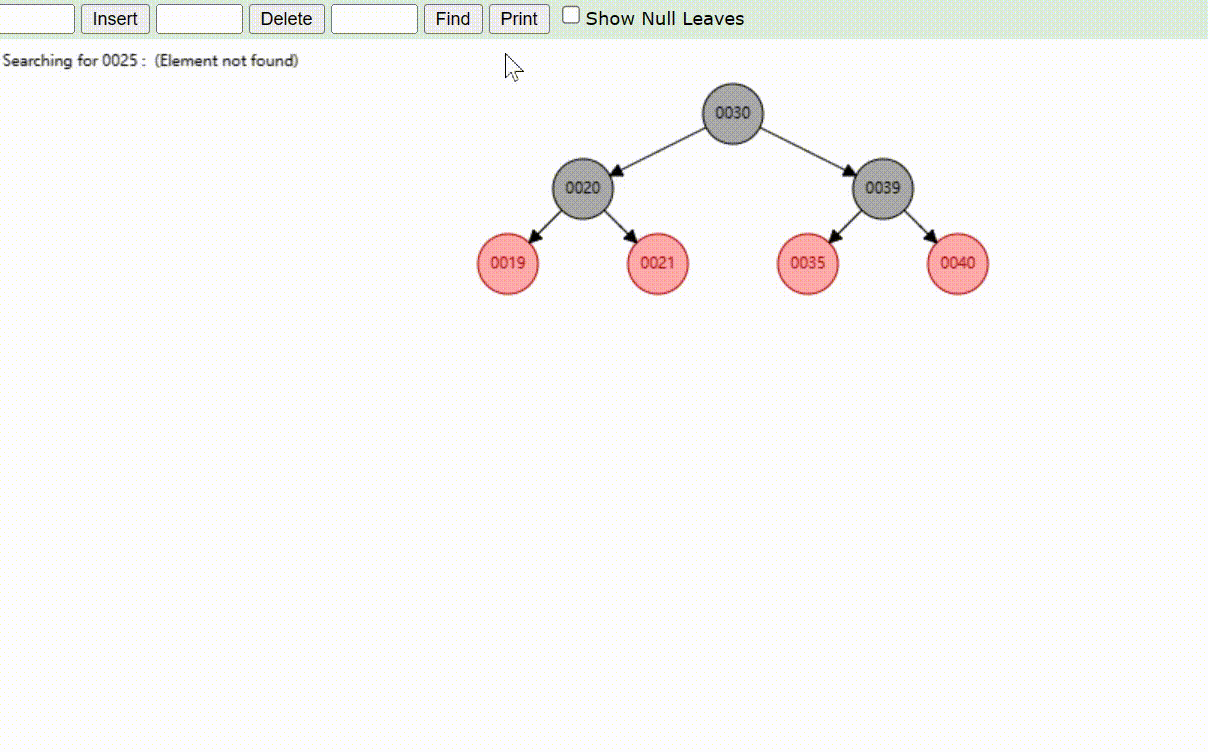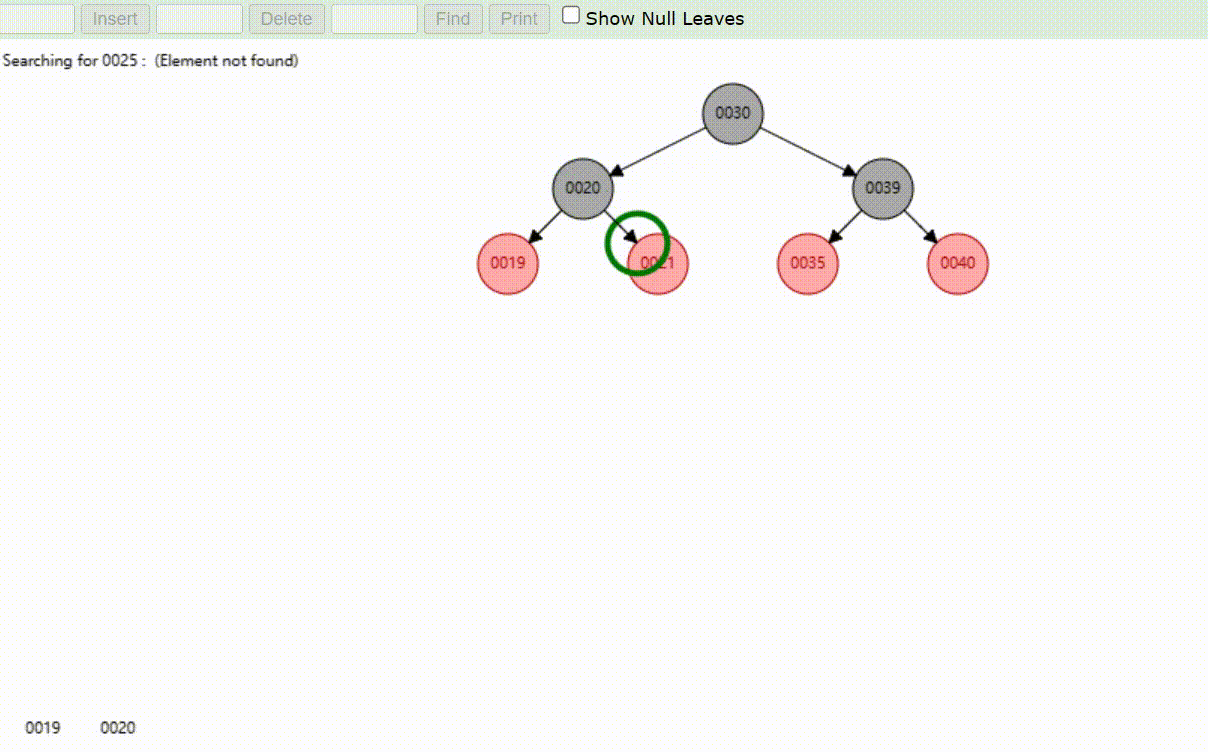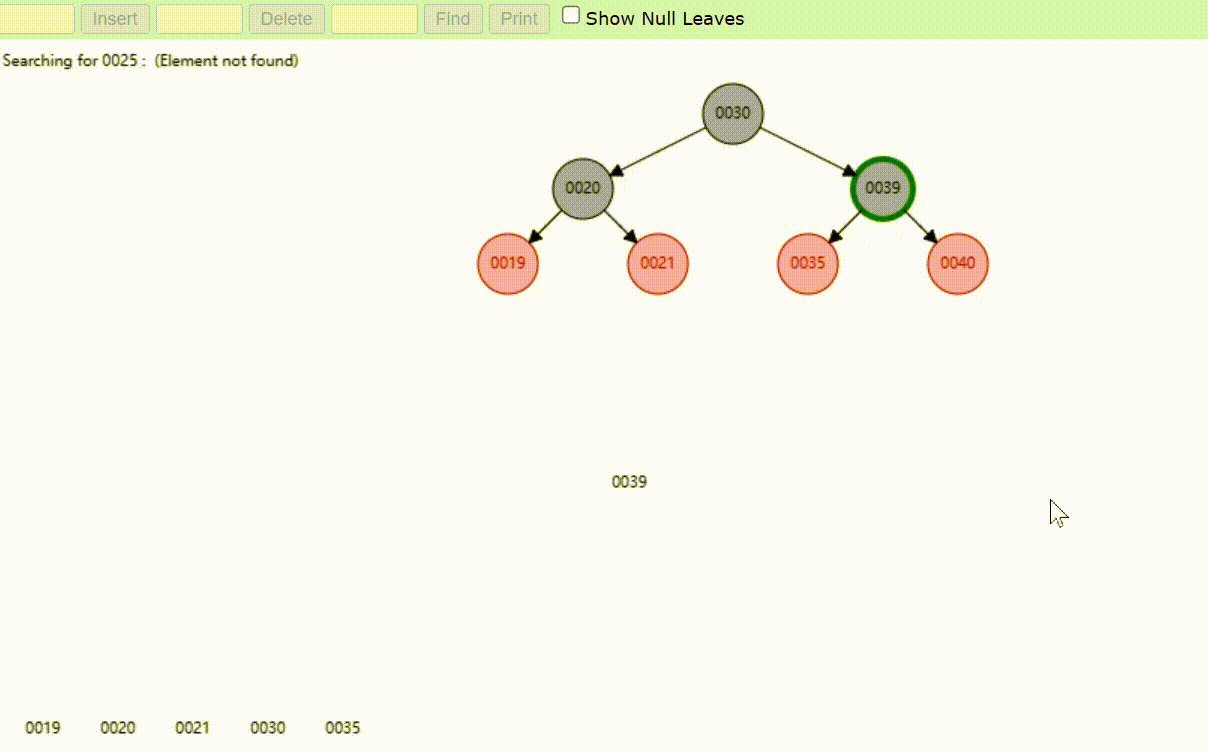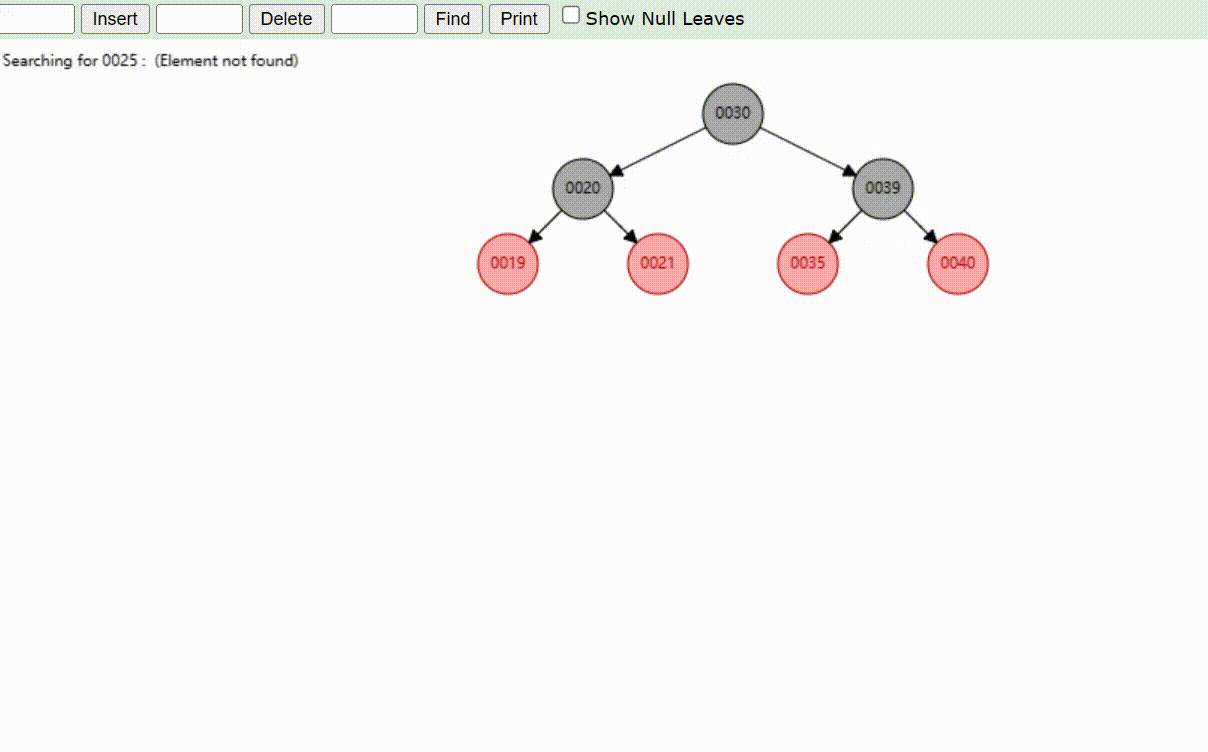
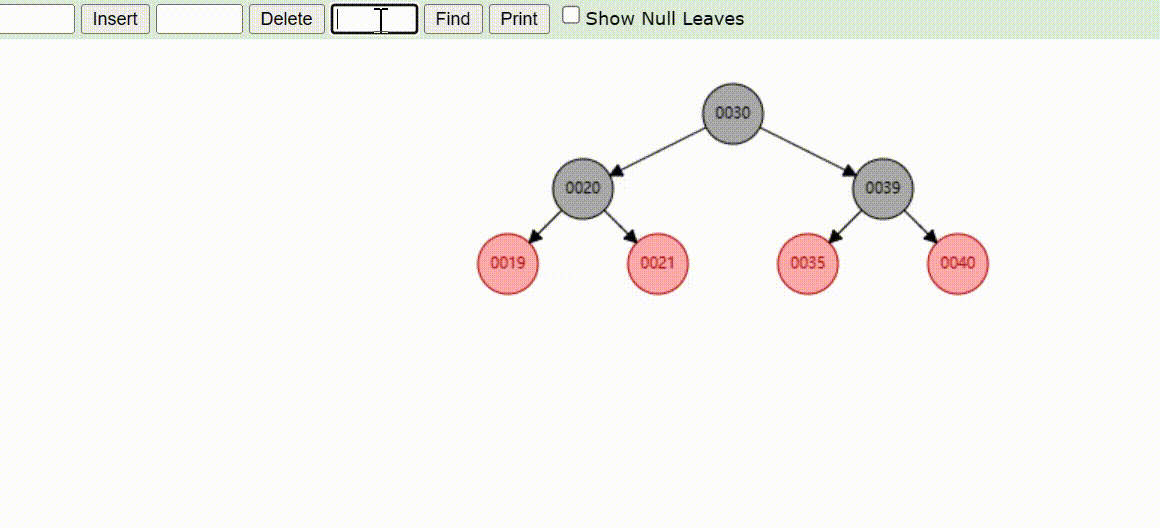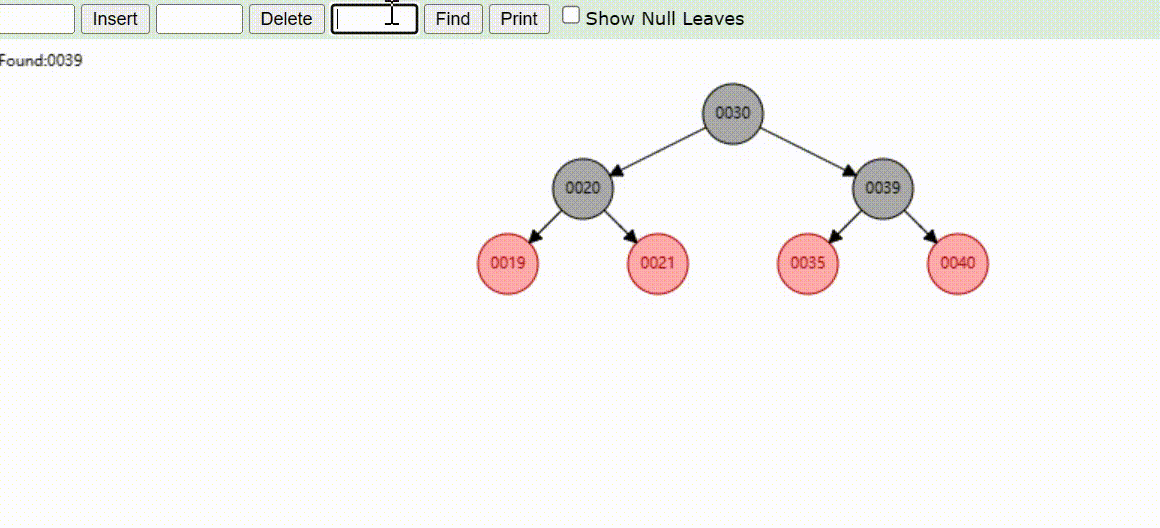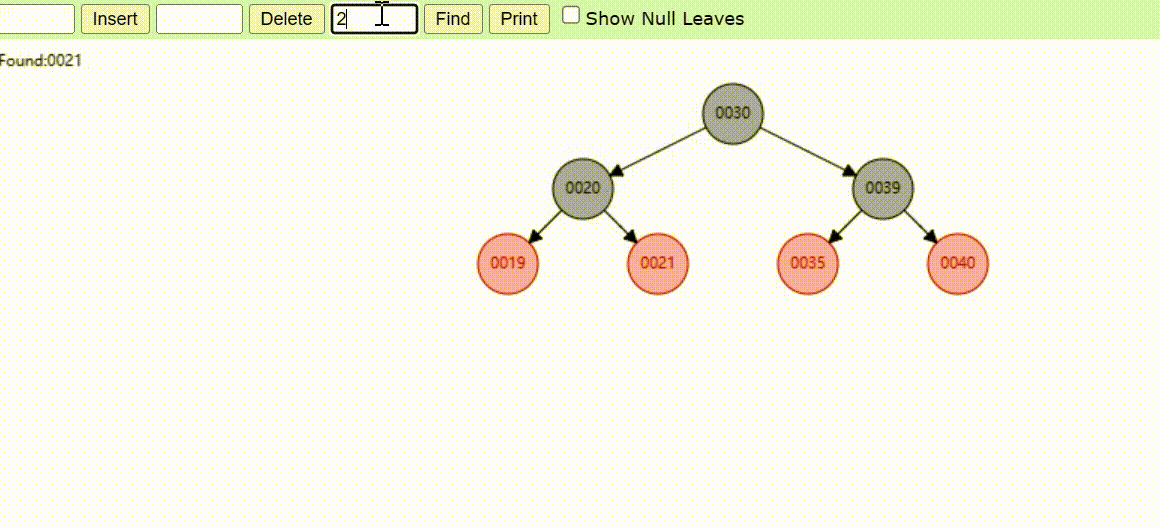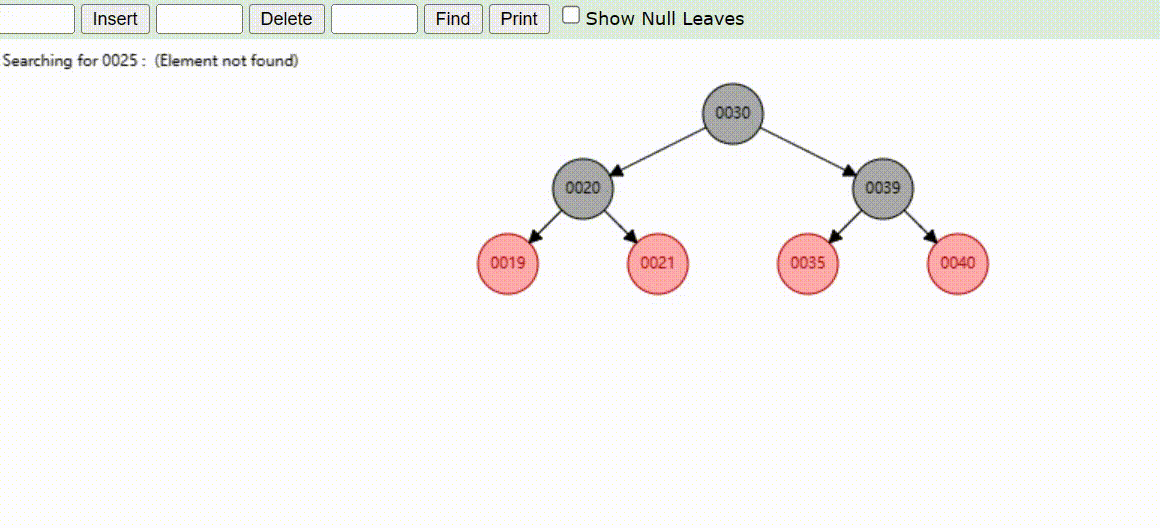
红黑树的数据查找(查找39 、21、25)
红黑树的数据删除(依次删除19、39、30)
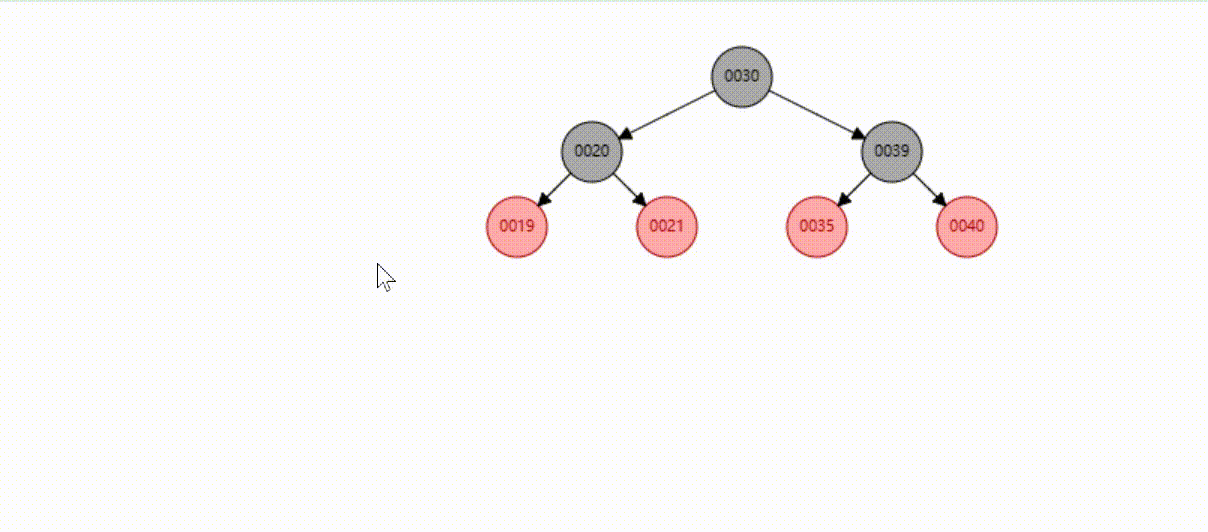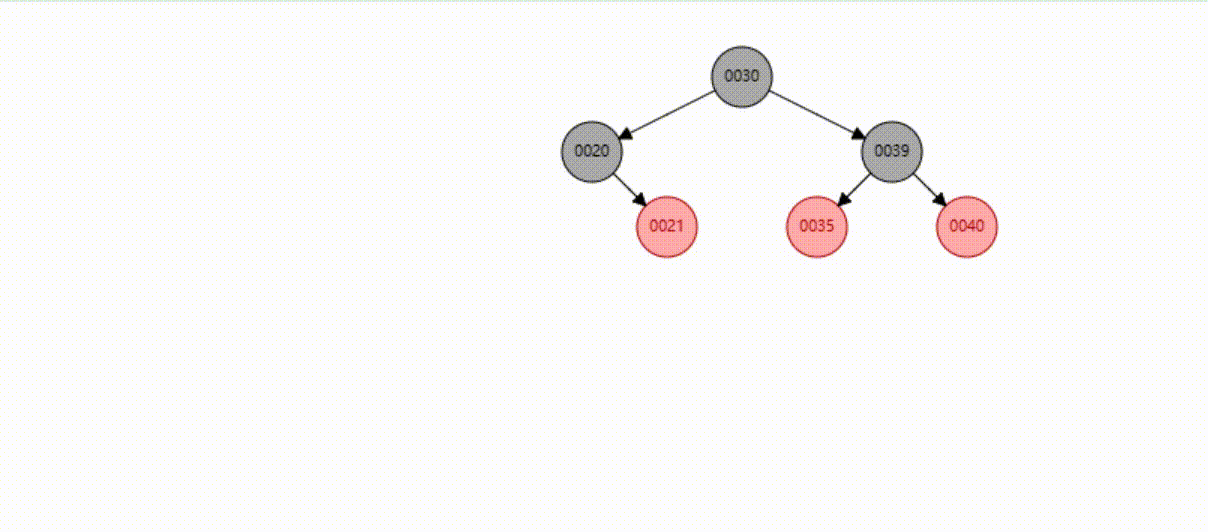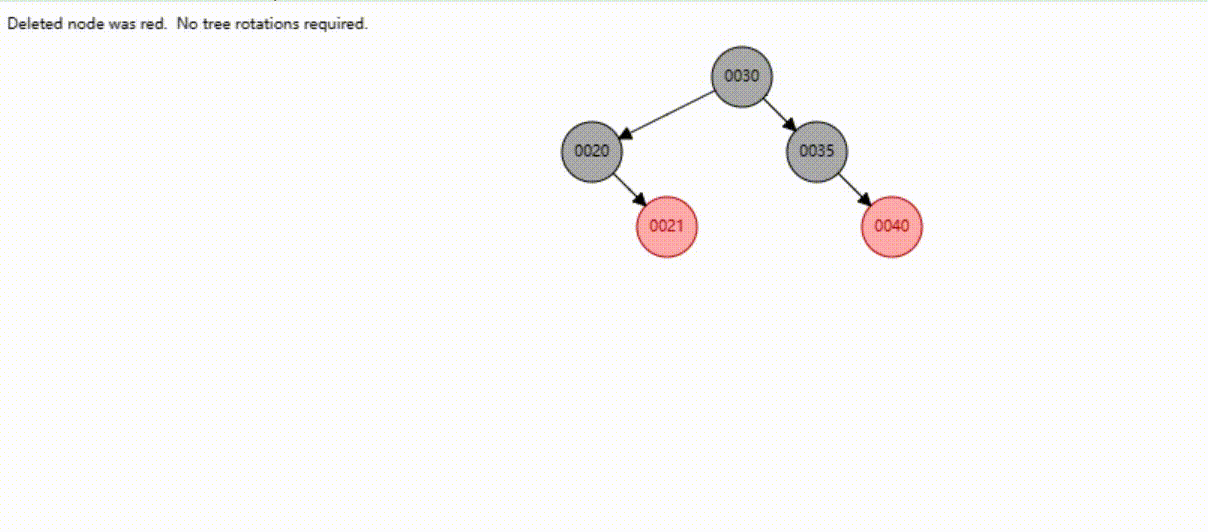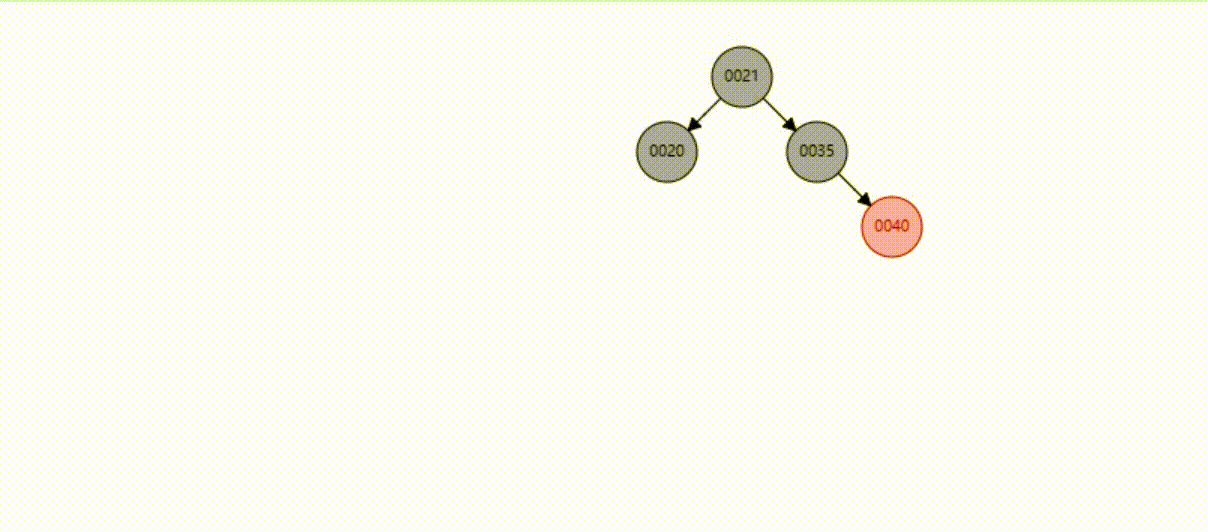
B-Tree树(多路平衡查找树)
二叉树一个Node节点只能够存储一个Key和一个Value,并且只有两个子节点;而多路树相比较而言一个Node节点能够存储更多的Key和Value,能够携带更多的子节点,建树高度会比二叉树要低
B-Tree树的一个节点能够存储多少Key和Value,可以有多少个子节点通过最大度数(MAX-Degree 也称为阶数)决定
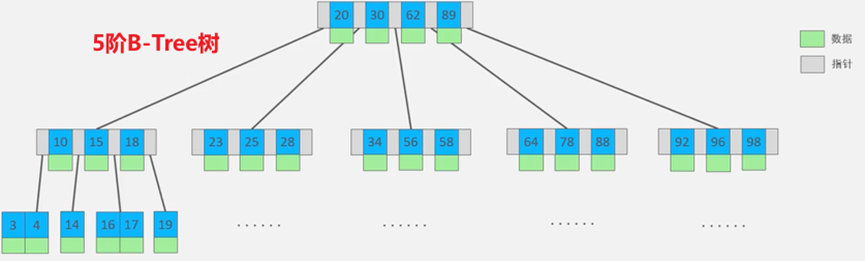
一个m阶的B-Tree树
树中的每个节点最多有m个子节点,m-1个Key和Value(两个子树的指针夹着一个Key和Value)
树的根节点至少有一个Key和Value,至少两个子节点
缺点
B树的叶子节点和非叶子节点都会保存数据,使得非叶子节点保存的指针量变小
如果存储大量的数据,需要增加树的高度,导致IO操作变多,查询性能变低
B-Tree树的工作原理
B-Tree树的数据插入Max-Degree为3(依次插入30、40、20、19、21、39、35)

B-Tree树的数据遍历
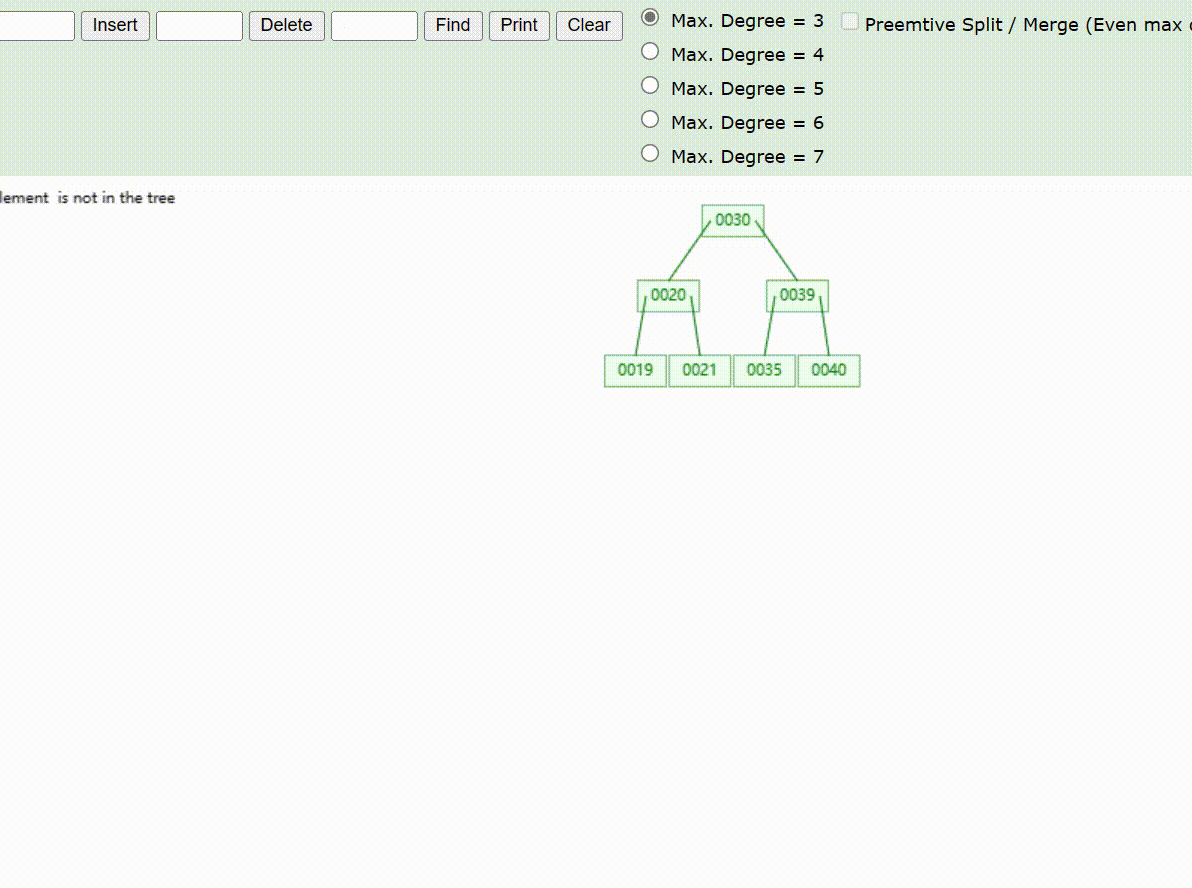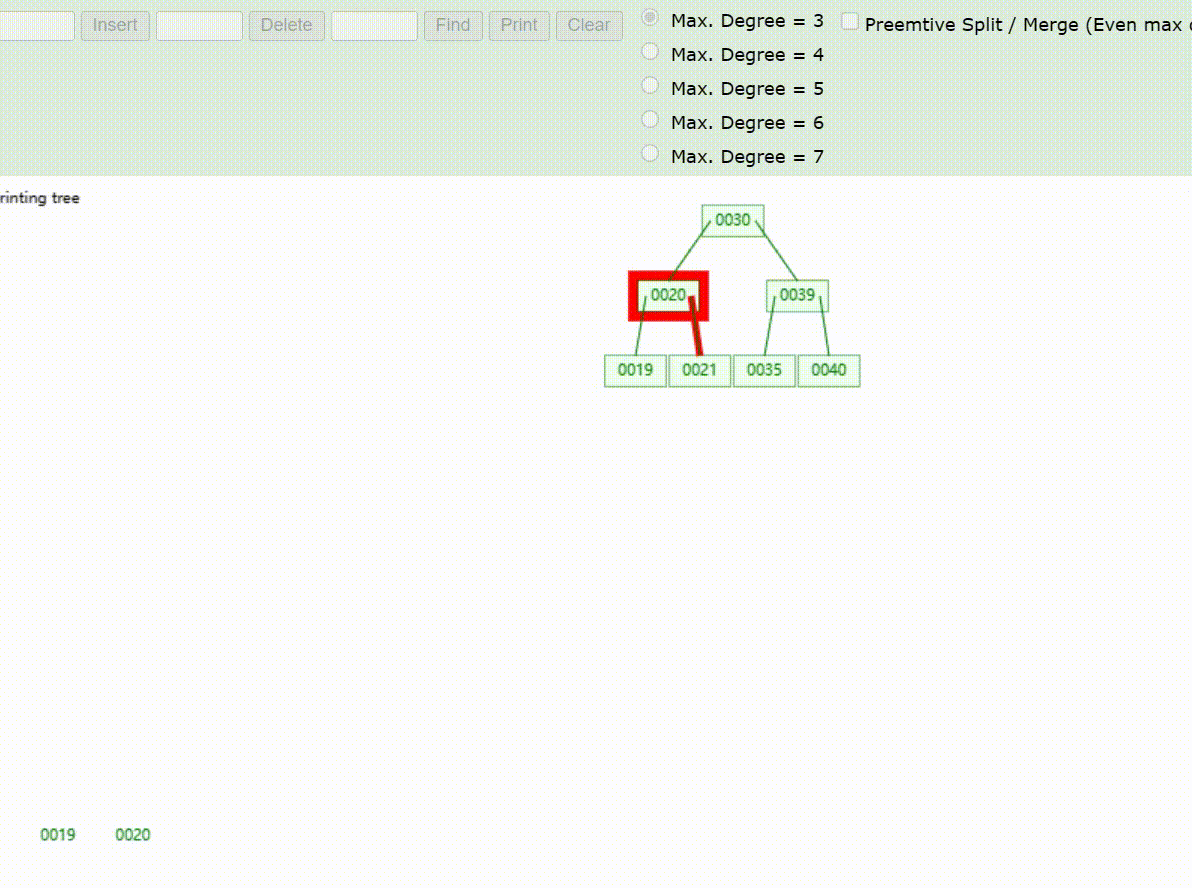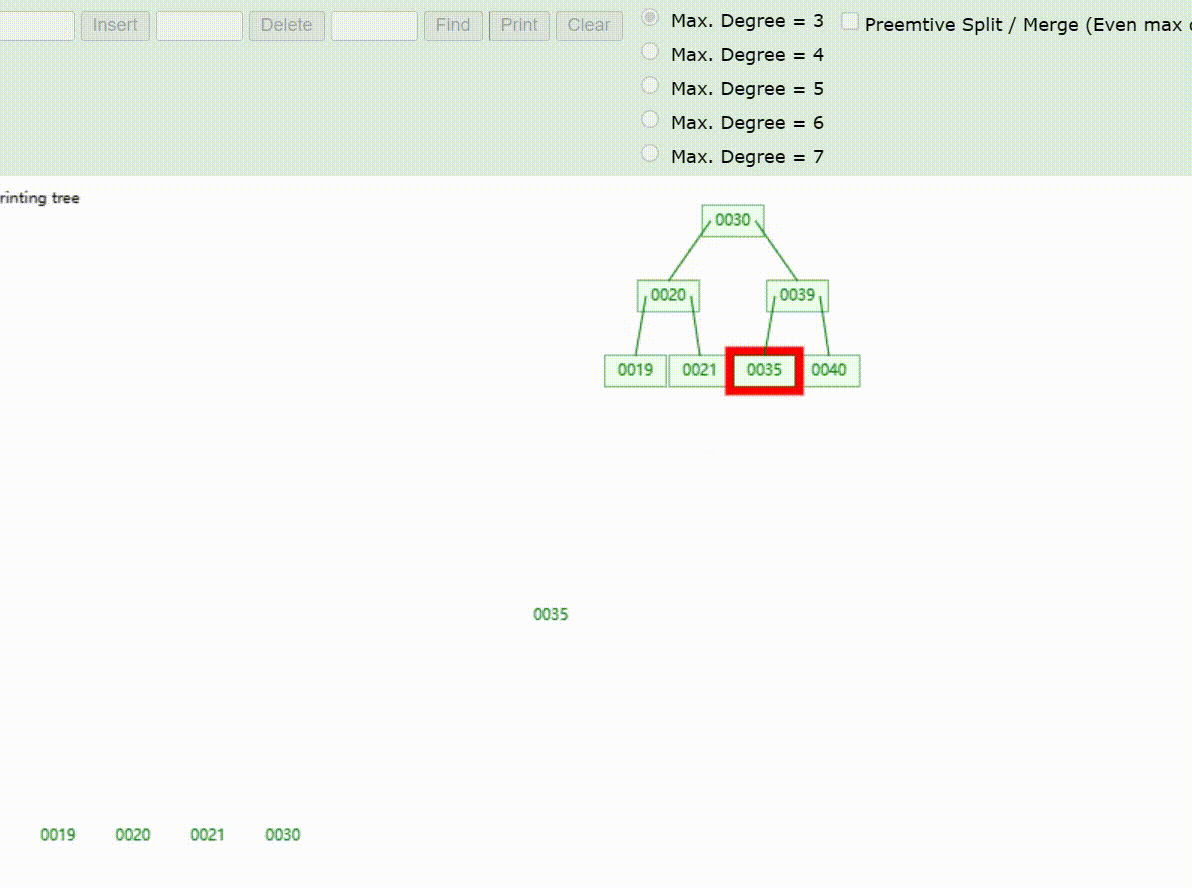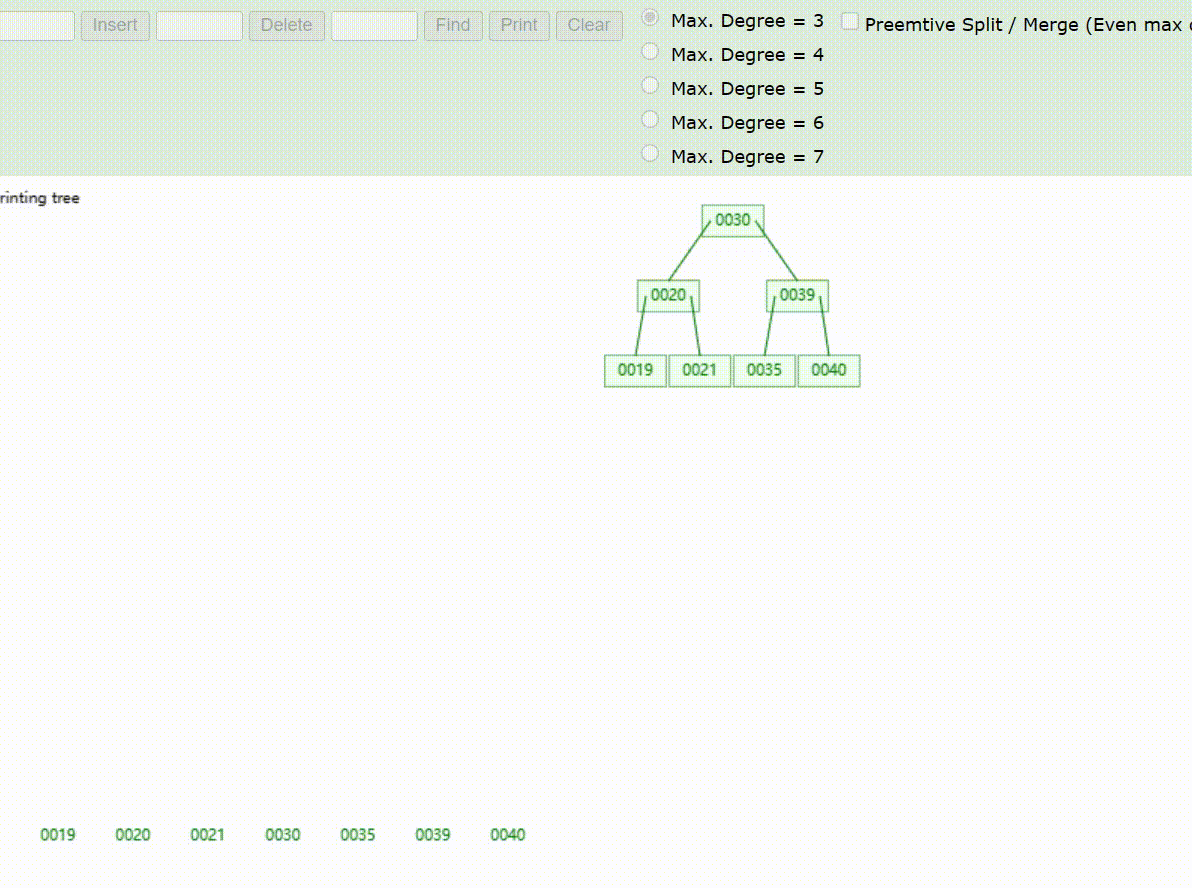
B-Tree树的数据查找(查找39 、21、25)
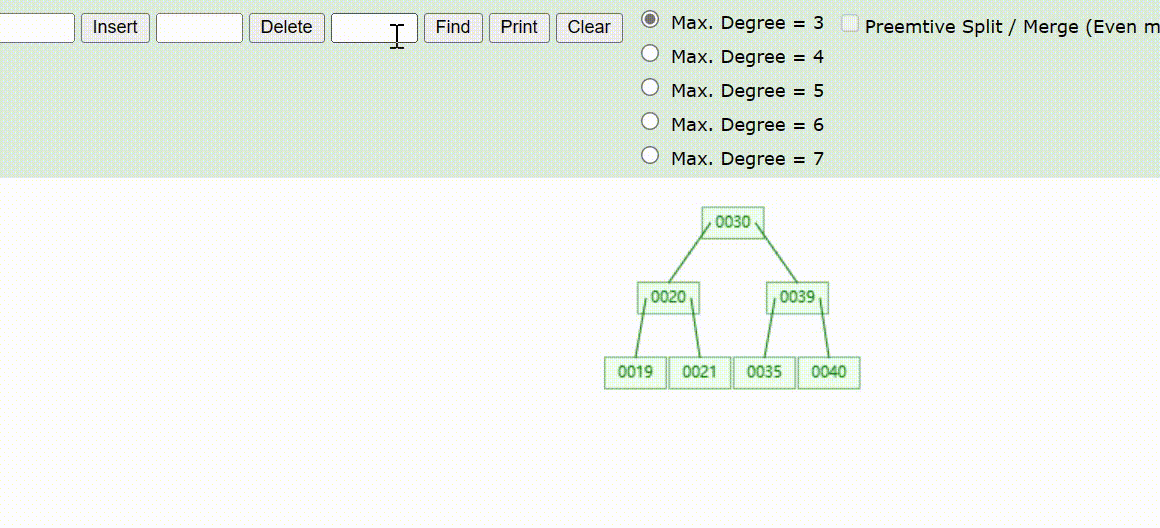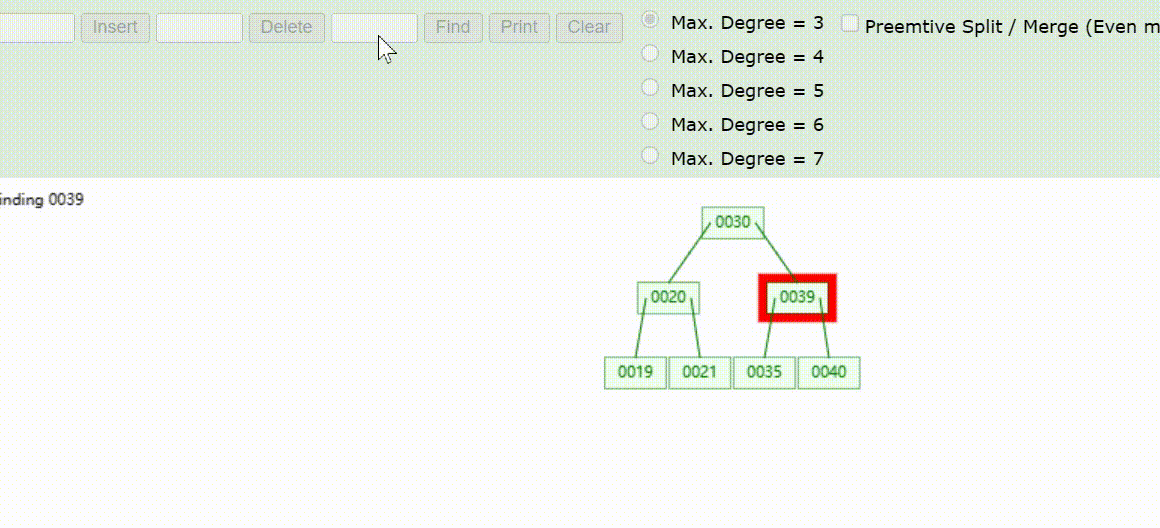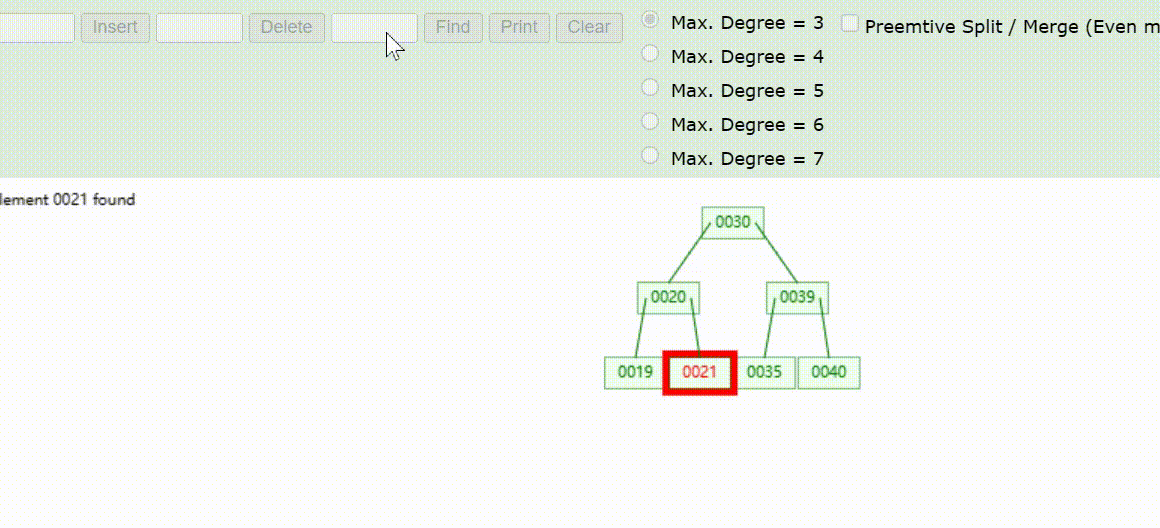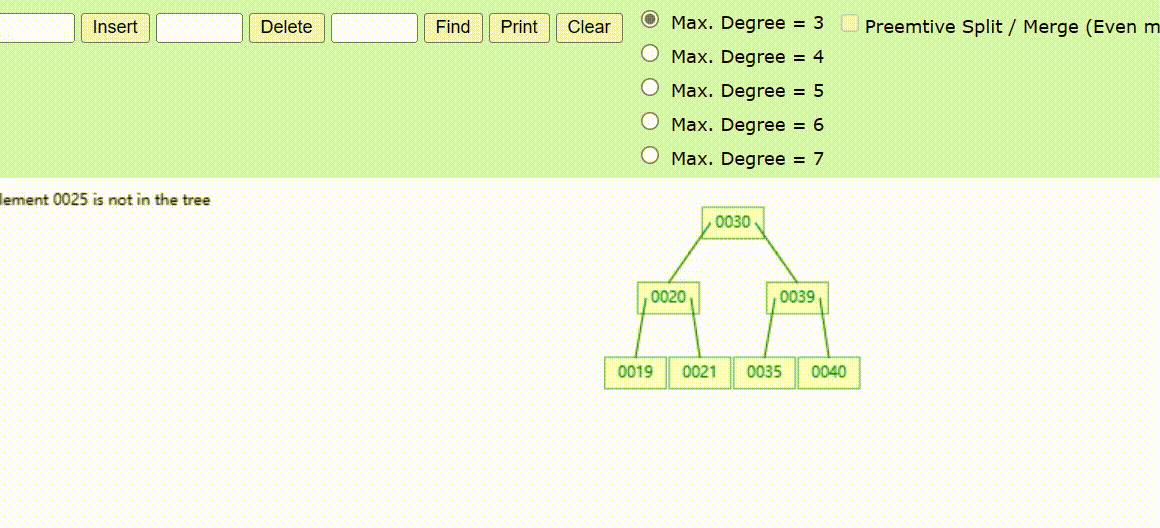
B-Tree树的数据删除(依次删除19、39、30)

B+Tree树
B+Tree树是B-Tree树的变种,也是一种多路搜索树,定义基本与B-Tree相同
B+Tree只有叶子节点存储数据,并且所有的元素都会出现在叶子节点中,所有叶子节点形成了一个单向链表;叶子节点将数据按照大小排列,并且相邻叶子节点之间按照大小排列
非叶子节点不存储数据,只存储Key,只是起到索引的作用,在相同的数据量下,B+Tree树更加矮壮
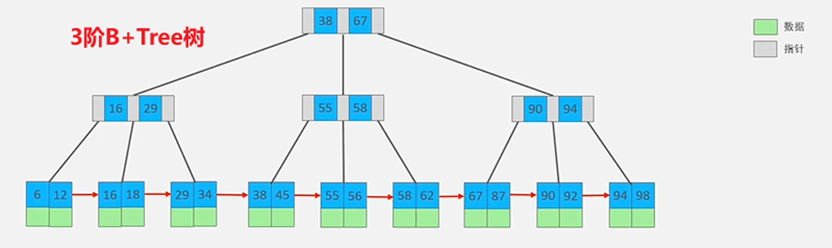
B-Tree树的工作原理
B+Tree树的数据插入Max-Degree为3(依次插入30、40、20、19、21、39、35)

B+Tree树的数据遍历
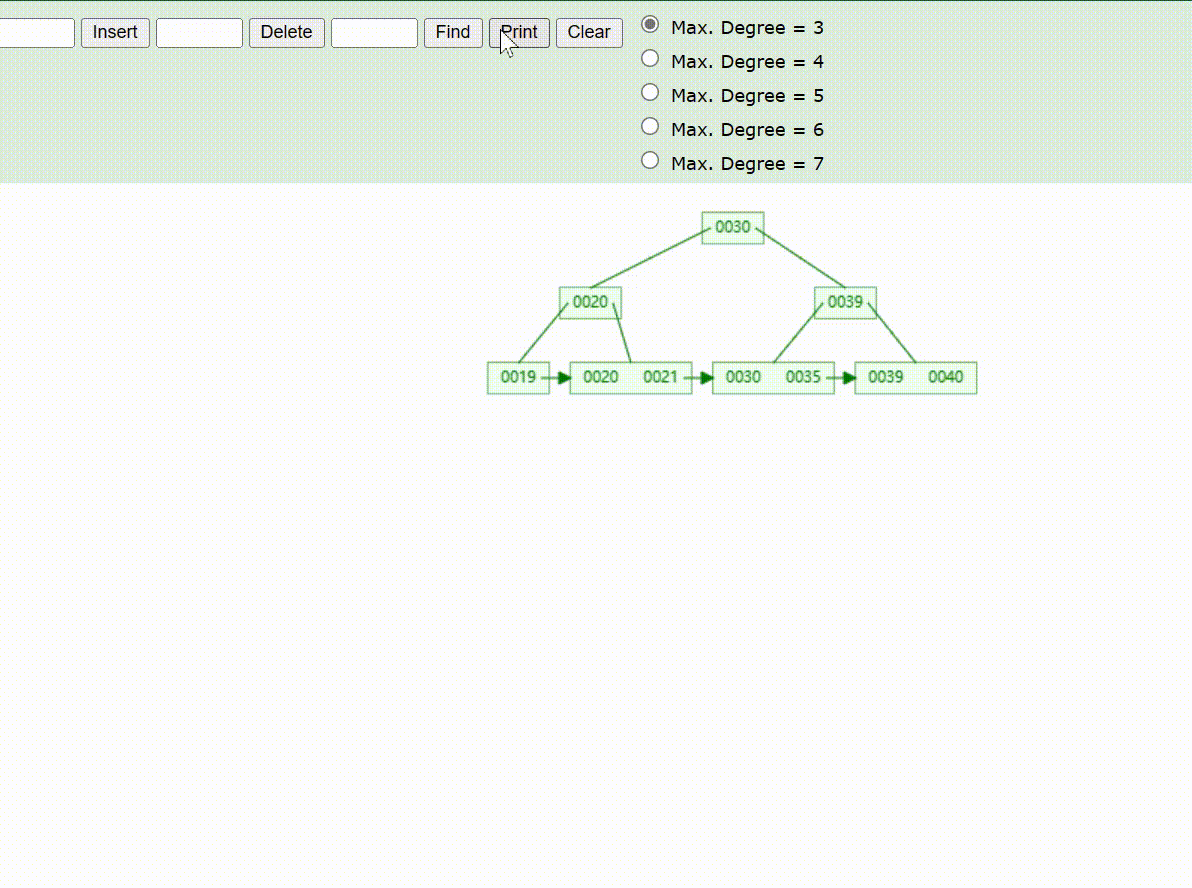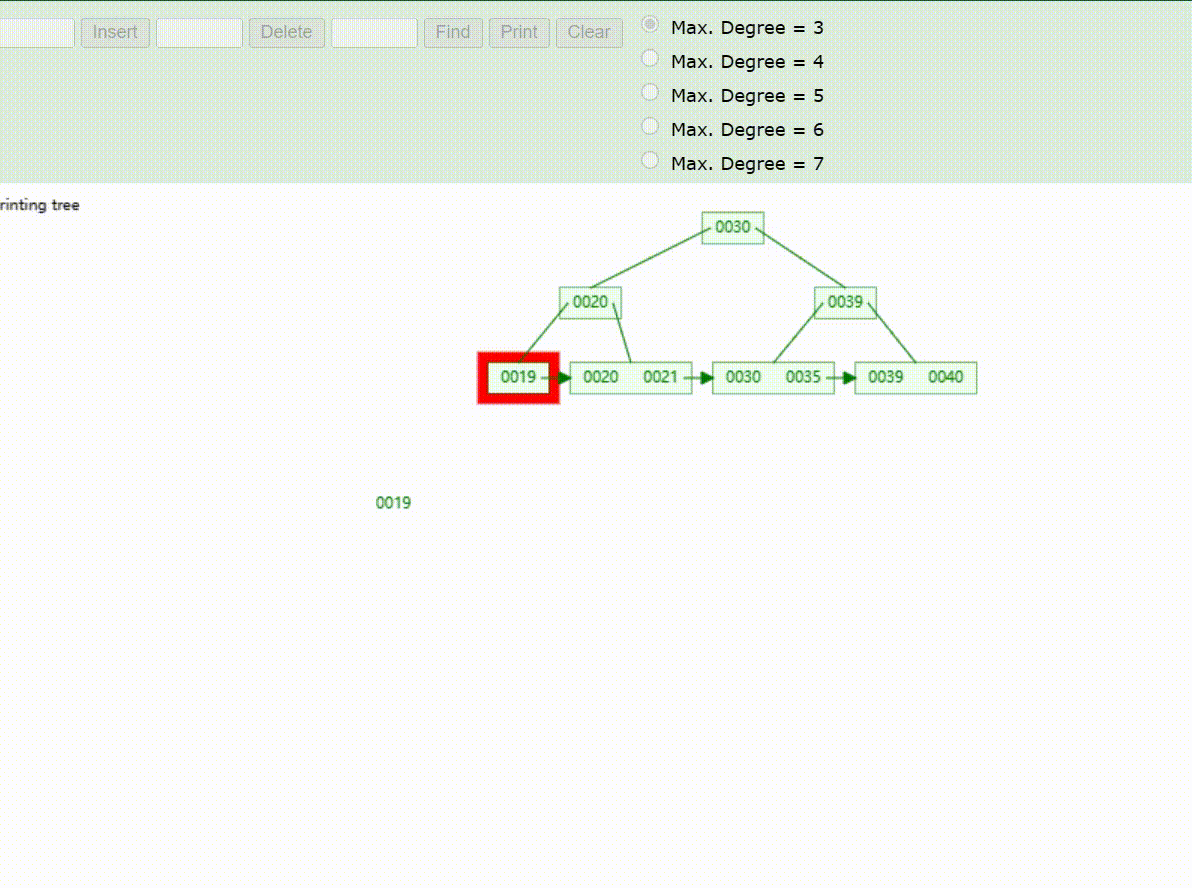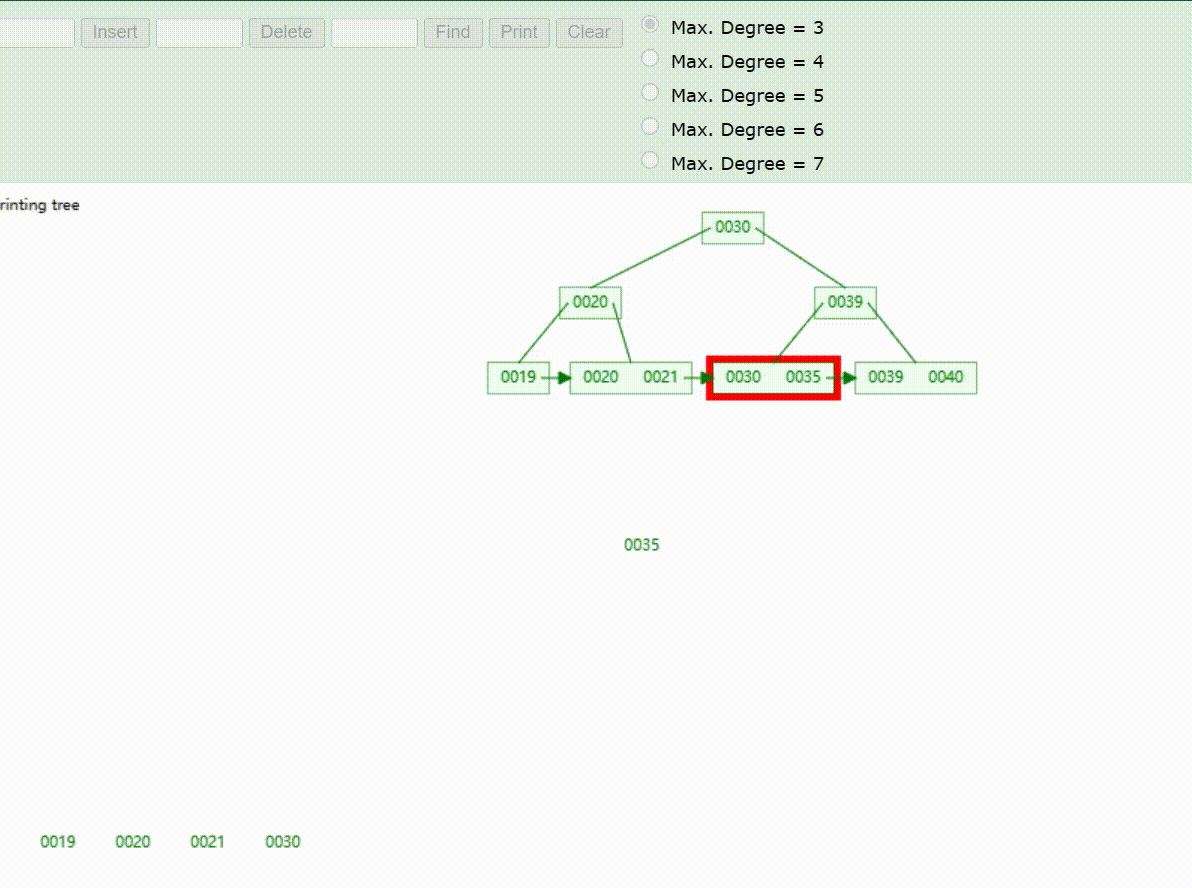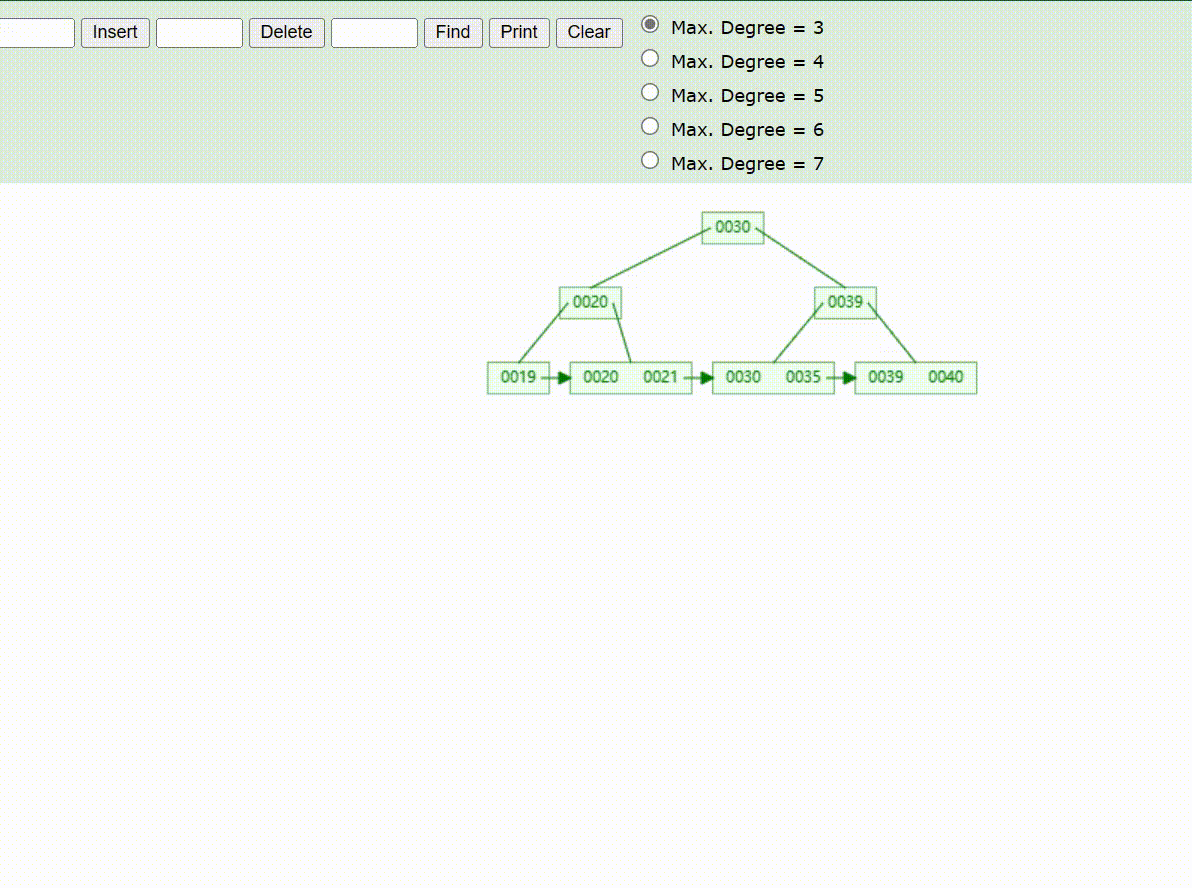
B+Tree树的数据查找(查找39 、21、25)
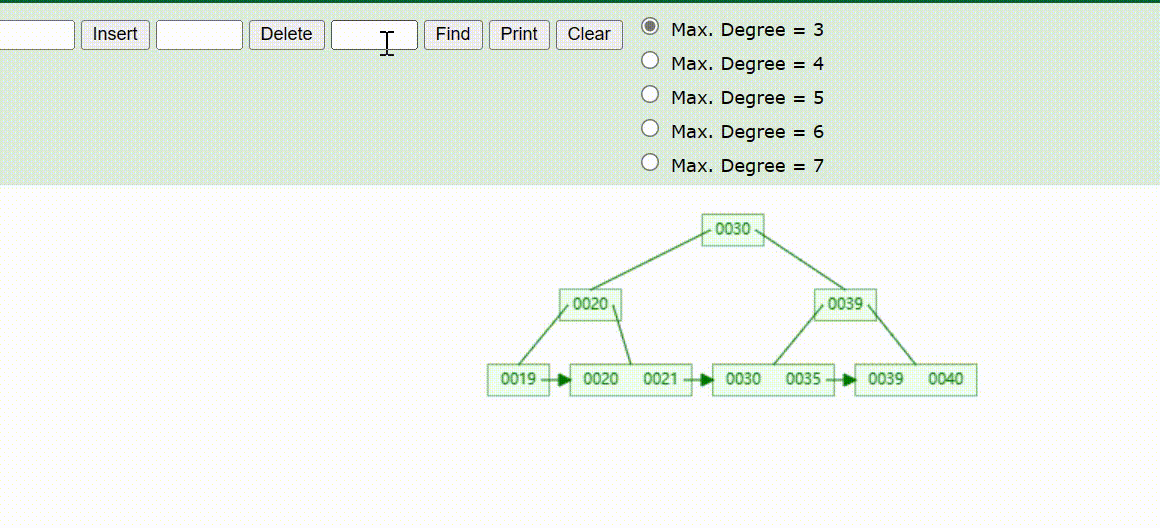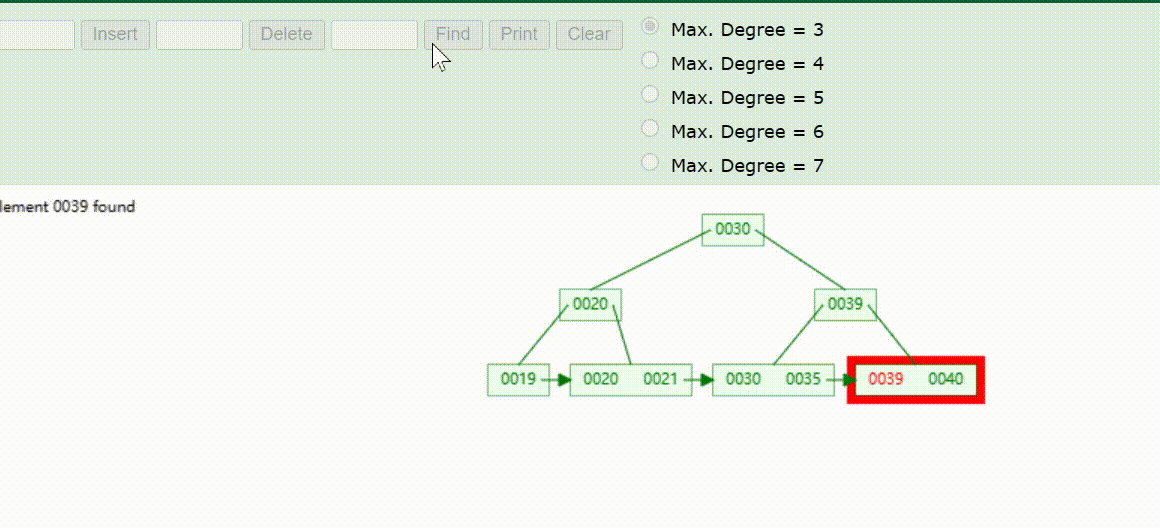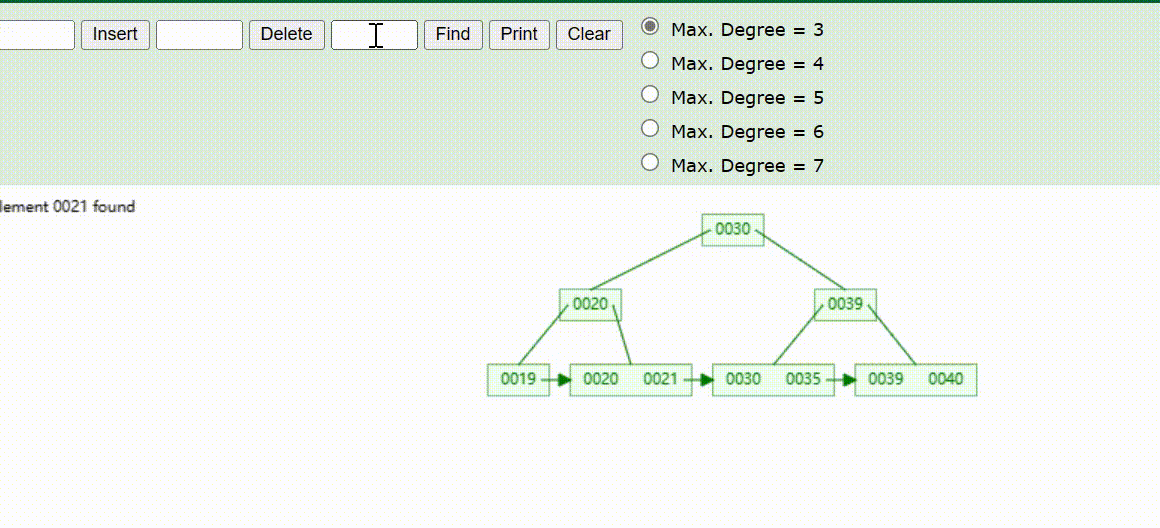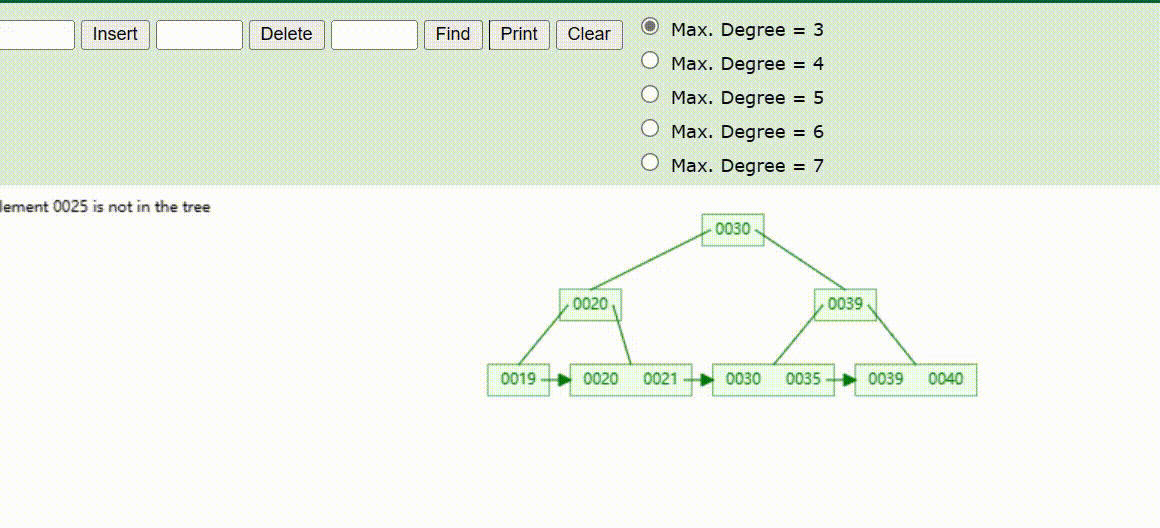
B+Tree树的数据删除(依次删除19、39、30)
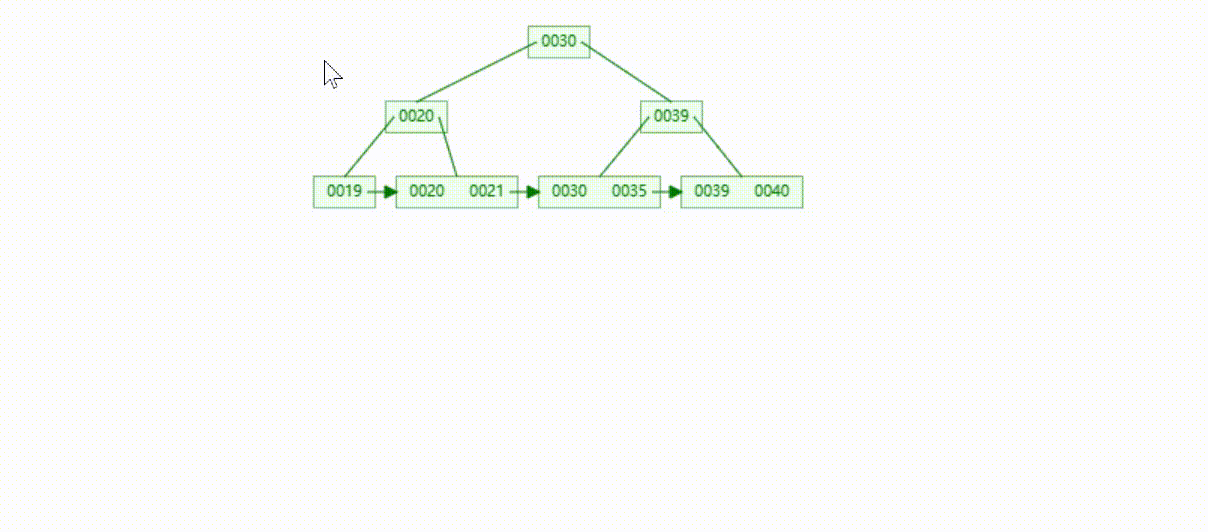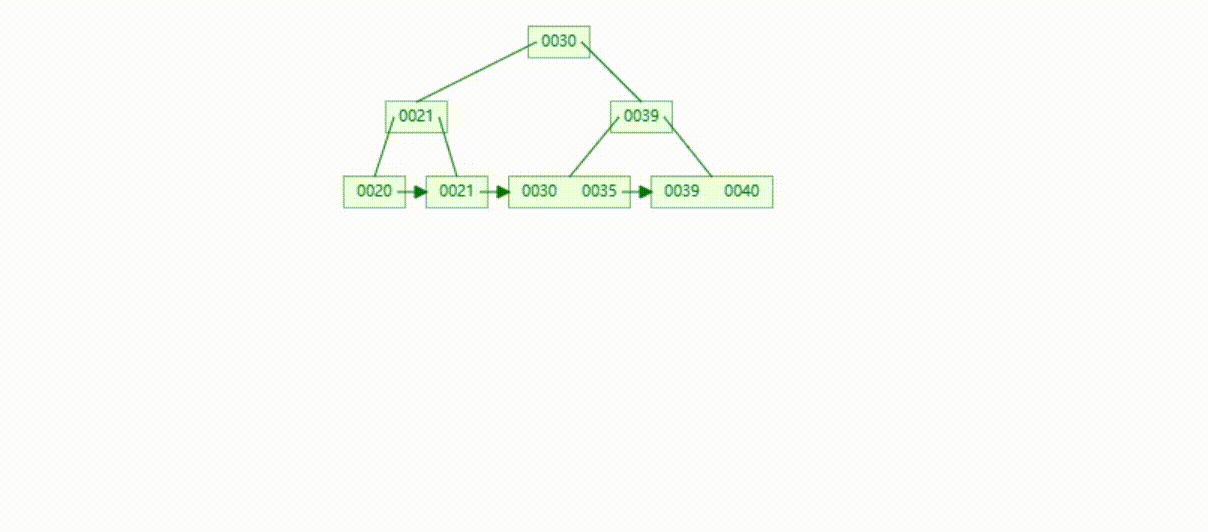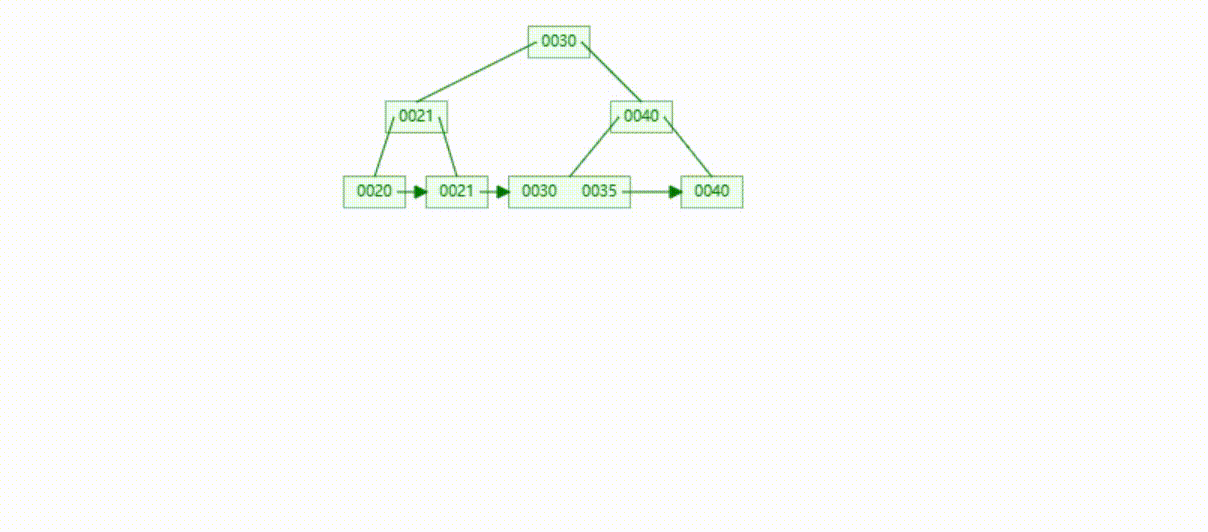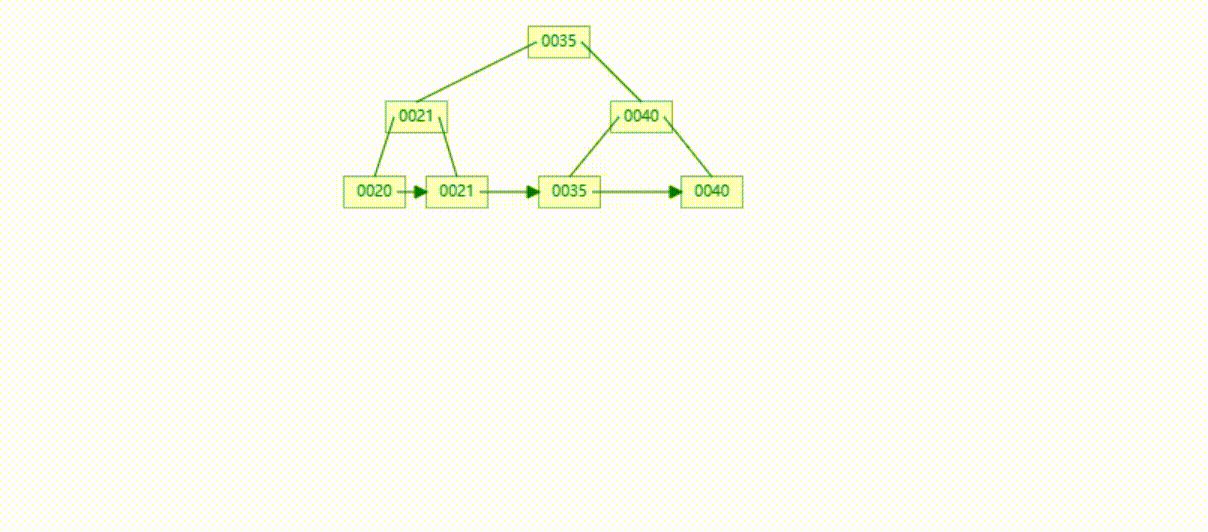
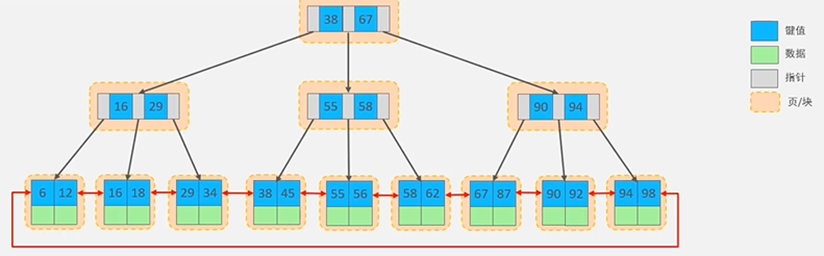
MySQL的B+Tree索引结构
MySQL的索引数据结构对经典的B+Tree进行了优化,在原B+Tree的基础上,增加了一个指向相邻叶子节点的链表指针,所有叶子节点形成了一个双向链表,提高了遍历速度
MySQL在查询是根据查询条件查询对应的键值(Key),然后将键值对应数据(Value)提取出来
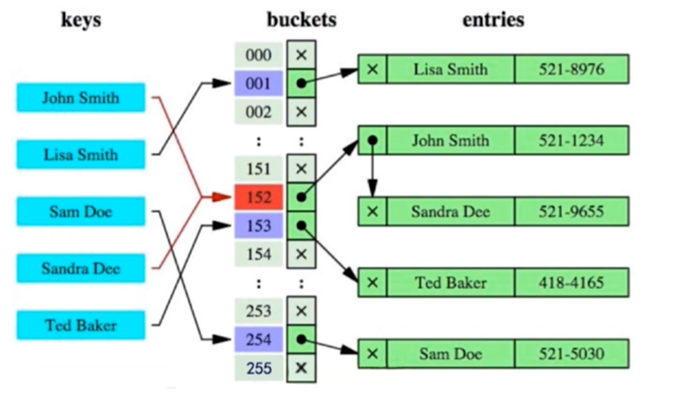
Hash索引结构
哈希索引就是采用一定的hash算法,将键值换算成新的Hash值,将哈希值映射到一个桶中,桶中存储了所有哈希值相同的数据行的指针,然后存储在Hash表中;
当查询时,MySQL会先通过哈希函数计算出查询条件的哈希值,在Hash表中查找对应的桶,然后在对应的桶中查找相应的数据行
哈希冲突
如果两个或多个键值,映射到同一个相同的槽位(桶),则他们就产生了hash冲突,通过链表解决
特点
- Hash索引只能够用于对等比较(=,in等),不支持范围查询(between,>,<等)
- 无法利用Hash索引完成排序操作;因为Hash索引中存放的是经过Hash计算后的Hash值,此值的大小并不一定和Hash运算之前的键值完全一样
- Hash索引无法避免表扫描,即每次都要全表扫描;因为Hash索引是将键值通过Hash运算之后,将其结果和对应的行指针信息存放在一个Hash表中,由于不同的索引键可能存在相同的Hash值,也就是哈希冲突,所以满足某个Hash键值的数据的记录跳数,无法直接从Hash索引中直接完成查询,还是要通过访问表中的实际数据进行比较,并得到相应的结果
- 对于联合索引,Hash不能使用部分索引键查询(要么全部使用,要么全部不使用)
- Hash只需要做一次运算,就可以找到该数据所在的桶;不像树结构那样从根、叶子节点的顺序来查找;所以Hash索引的查询效率理论上是要高于B+Tree的;不过对于存在大量Hash值相同的情况下,性能不一定比B+Tree高
Full-Text索引
通过建立倒排索引(Inverted Index)构建Full-Text索引,提高数据的检索效率
倒排索引是一种将文档中的单词/汉字映射到其出现位置的数据结构,主要用来解决判断字段的值中 是否包含 某字符/汉字的问题
我们对于简单业务或者数据量小的业务,可以通过Like()关键字来判断;但是对于大数据量业务,使用Like效率会大大降低
不同存储索引对Full-Text索引的支持
在MySQL5.6版本之前,只有MYISAM存储引擎支持全文索引
在MySQL5.6版本之后,InnoDB能够支持全文索引;不过只支持对英文的全文索引,不支持中文的全文索引;后续通过内置分词器(ngram)来支持中文索引
配置ngram的最小长度
在MySQL的配置文件中添加以下字段
ft_min_word_len = 2 #此最小长度就是分词的最小长度,默认为2
即:对于一段语句,可以分为多个汉字组,每个汉字组最少都有2个汉字
我想学习数据库 可以分词为: 我想 学习 数据库 三个组
一般不会将ngram设置的很小,如果很小的话会占用大量的空间,因此我们一般都不修改此最小长度,就默认为2
全文索引的流程
用户输入要查找的内容 → SQL执行引擎 → ngram对查找的内容进行分词 → 把分词后的词依次的去倒排索引中去查找 → 将相应的记录返回
分词器ngram在建立索引时会对字段中的值进行分词;在进行查询时也会对要查找的内容分词
R-Tree索引
构建空间索引有多种数据结构,例如四叉树、R-Tree树
在MySQL中是通过R-Tree树来构建空间索引的,是一种加快空间数据查询速度的技术
R-tree将空间数据分割成一系列矩形区域,每个节点可以表示一个矩形区域,同时可以包含其他节点或数据项。这种层级结构允许MySQL在空间查询中更快地定位所需的数据,减少搜索范围,从而提高查询性能
例如:
一个表中的某字段存储着一个地方餐馆的经纬度位置信息,现在我们需要根据我们的位置,找附近1公里的餐馆
我们可以通过计算我们的位置,找到附近1公里范围内的经纬度范围,然后查询表中的满足此经纬度的值;为了加快检索效率,我们就可以对存储经纬度位置信息的字段建立空间索引
R-Tree的构建过程——R树是把B树的思想扩展到了多维空间
1、数据划分
所有的数据项也成为对象(点、线或面)都被视为一个单独的矩形
2、构建叶子节点(叶子节点是R树的底层节点)
将划分好的矩形进行分组,并构建叶子节点;每个叶子节点包含多个对象及其对应的矩形
3、合并叶子节点
当叶子节点的数目超过了R-Tree规定的最大容量,此时R树会尝试合并相邻的叶子节点来减少树的高度和提高查询效率
4、构建非叶子节点
将合并后叶子构建为新的非叶子节点;非叶子节点也是一个矩形,包含了其所有子节点的矩形范围
5、递归构建
重复上述的操作,知道构建出整个R树的根节点(R树的最顶层节点,将包含所有的数据范围)
具体R树的构建方式可以参考以下文章
从B树、B+树、B*树谈到R 树_v_JULY_v的博客-CSDN博客![]() https://blog.csdn.net/v_JULY_v/article/details/6530142
https://blog.csdn.net/v_JULY_v/article/details/6530142
)










的大小呢?)
附带AXI4协议校验IP使用方法)






