URAL1519 Formula 1 —— 插头DP

题目链接：https://vjudge.net/problem/URAL-1519

 

1519. Formula 1

Time limit: 1.0 second
Memory limit: 64 MB

Background

Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic games of 20**, it is well-known, that the city will conduct one of the Formula 1 events. Surely, for such an important thing a new race circuit should be built as well as hotels, restaurants, international airport - everything for Formula 1 fans, who will flood the city soon. But when all the hotels and a half of the restaurants were built, it appeared, that at the site for the future circuit a lot of gophers lived in their holes. Since we like animals very much, ecologists will never allow to build the race circuit over the holes. So now the mayor is sitting sadly in his office and looking at the map of the circuit with all the holes plotted on it.

Problem

Who will be smart enough to draw a plan of the circuit and keep the city from inevitable disgrace? Of course, only true professionals - battle-hardened programmers from the first team of local technical university!.. But our heroes were not looking for easy life and set much more difficult problem: "Certainly, our mayor will be glad, if we find how many ways of building the circuit are there!" - they said.

It should be said, that the circuit in Vologda is going to be rather simple. It will be a rectangle N*M cells in size with a single circuit segment built through each cell. Each segment should be parallel to one of rectangle's sides, so only right-angled bends may be on the circuit. At the picture below two samples are given for N = M = 4 (gray squares mean gopher holes, and the bold black line means the race circuit). There are no other ways to build the circuit here.

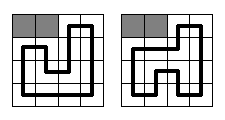
Input

The first line contains the integer numbers N and M (2 ≤ N, M ≤ 12). Each of the next N lines contains M characters, which are the corresponding cells of the rectangle. Character "." (full stop) means a cell, where a segment of the race circuit should be built, and character "*" (asterisk) - a cell, where a gopher hole is located. There are at least 4 cells without gopher holes.

Output

You should output the desired number of ways. It is guaranteed, that it does not exceed 263-1.

Samples

input	output
4 4 **.. .... .... ....	2
4 4 .... .... .... ....	6

Problem Author: Nikita Rybak, Ilya Grebnov, Dmitry Kovalioff
Problem Source: Timus Top Coders: Third Challenge

Tags: none  (hide tags for unsolved problems)

 

 

题意：

用一个回路去走完所有的空格，问有多少种情况？

 

题解：

1.学习插头DP的必经之路：《基于连通性状态压缩的动态规划问题》

2.HDU1693 Eat the Trees 这题的加强版。

3.相对于HDU1693，由于此题限制了只能用一个回路，所以在处理的时候，需要记录轮廓线上，每个插头分别属于哪个连通分量的，以此避免形成多个回路。

4.由于m<=12，故连通分量最多为12/2 = 6个，再加上没有插头的情况，所以轮廓线上每个位置的状态共有7种，为了加快速度，我们采用8进制对其进行压缩。

5.对于一条轮廓线，最多有：8^(12+1)种状态，所以直接用数组进行存储或者直接枚举所以状态是不可行的。但我们知道其中有许多状态是无效的，所以我们采用哈希表来存在有效状态，即能解决空间有限的问题，还能减少直接枚举所需要的时间花费。

 

 

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 1e5;
const int HASH = 1e4;

int n, m, last_x, last_y;
bool maze[13][13];

struct  //注意哈希表的大小
{
    int size, head[HASH], next[MAXN];
    LL state[MAXN], sum[MAXN];

    void init()
    {
        size = 0;
        memset(head, -1, sizeof(head));
    }

    void insert(LL status, LL Sum)
    {
        int u = status%HASH;
        for(int i = head[u]; i!=-1; i = next[i])
        {
            if(state[i]==status)
            {
                sum[i] += Sum;
                return;
            }
        }
        state[size] = status;   //头插法
        sum[size] = Sum;
        next[size] = head[u];
        head[u] = size++;
    }

}Hash_map[2];

struct
{
    int code[13];   //用于记录轮廓线上每个位置的插头状态
    LL encode(int m)    //编码：把轮廓线上的信息压缩到一个longlong类型中
    {
        LL status = 0;
        int id[13], cnt = 0;
        memset(id, -1, sizeof(id));
        id[0] = 0;
        for(int i = m; i>=0; i--)   //从高位到低位。为每个连通块重新编号，采用最小表示法。
        {
            if(id[code[i]]==-1) id[code[i]] = ++cnt;
            code[i] = id[code[i]];
            status <<= 3;   //编码
            status += code[i];
        }
        return status;
    }

    void decode(int m, LL status)  //解码：将longlong类型中轮廓线上的信息解码到数组中
    {
        memset(code, 0, sizeof(code));
        for(int i = 0; i<=m; i++)   //从低位到高位
        {
            code[i] = status&7;
            status >>= 3;
        }
    }

    void shift(int m)   //左移：在每次转行的时候都需要执行。
    {
        for(int i = m-1; i>=0; i--)
            code[i+1] = code[i];
        code[0] = 0;
    }

}Line;

void transfer_blank(int i, int j, int cur)
{
    for(int k = 0; k<Hash_map[cur].size; k++)   //枚举上一个格子所有合法的状态
    {
        LL status = Hash_map[cur].state[k]; //得到状态
        LL Sum = Hash_map[cur].sum[k];      //得到数量
        Line.decode(m, status);             //对状态进行解码
        int up = Line.code[j];         //得到上插头
        int left = Line.code[j-1];     //得到下插头

        if(!up && !left)        //没有上、左插头，新建分量
        {
            if(maze[i+1][j] && maze[i][j+1])    //如果新建的两个插头所指向的两个格子可行，新建的分量才合法
            {
                Line.code[j] = Line.code[j-1] = 6;  //为新的分量编号，最大的状态才为6
                Hash_map[cur^1].insert(Line.encode(m), Sum);
            }
        }
        else if( (left&&!up) || (!left&&up) )   //仅有其中一个插头，延续分量
        {
            int line = left?left:up;    //记录是哪一个插头
            if(maze[i][j+1])    //往右延伸
            {
                Line.code[j-1] = 0;
                Line.code[j] = line;
                Hash_map[cur^1].insert(Line.encode(m), Sum);
            }
            if(maze[i+1][j])        //往下延伸
            {
                Line.code[j-1] = line;
                Line.code[j] = 0;
                if(j==m) Line.shift(m);
                Hash_map[cur^1].insert(Line.encode(m), Sum);
            }
        }
        else    //上、左插头都存在，尝试合并。
        {
            if(up!=left)    //如果两个插头属于两个联通分量，那么就合并
            {
                Line.code[j] = Line.code[j-1] = 0;
                for(int t = 0; t<=m; t++)   //随便选一个编号最为他们合并后分量的编号
                    if(Line.code[t]==up)
                        Line.code[t] = left;
                if(j==m) Line.shift(m);
                Hash_map[cur^1].insert(Line.encode(m), Sum);
            }
            else if(i==last_x && j==last_y) //若两插头同属一个分量，则只能在最后的可行格中合并，否则会出现多个联通分量
            {
                Line.code[j] = Line.code[j-1] = 0;
                if(j==m) Line.shift(m);
                Hash_map[cur^1].insert(Line.encode(m), Sum);
            }
        }
    }
}

void transfer_block(int i, int j, int cur)
{
    for(int k = 0; k<Hash_map[cur].size; k++)
    {
        LL status = Hash_map[cur].state[k]; //得到状态
        LL Sum = Hash_map[cur].sum[k];      //得到数量
        Line.decode(m, status);
        Line.code[j] = Line.code[j-1] = 0;
        if(j==m) Line.shift(m);
        Hash_map[cur^1].insert(Line.encode(m), Sum);
    }
}

int main()
{
    char s[15];
    while(scanf("%d%d", &n, &m)!=EOF)
    {
        memset(maze, false, sizeof(maze));
        for(int i = 1; i<=n; i++)
        {
            scanf("%s", s+1);
            for(int j = 1; j<=m; j++)
            {
                if(s[j]=='.')
                {
                    maze[i][j] = true;
                    last_x = i;         //记录最后一个可行格
                    last_y = j;
                }
            }
        }

        int cur = 0;
        Hash_map[cur].init();   //初始化
        Hash_map[cur].insert(0, 1); //插入初始状态
        for(int i = 1; i<=n; i++)
        for(int j = 1; j<=m; j++)
        {
            Hash_map[cur^1].init();
            if(maze[i][j])
                transfer_blank(i, j, cur);
            else
                transfer_block(i, j ,cur);
            cur ^= 1;
        }

        LL last_status = 0; //最后的轮廓线就是最后一行，且每个位置都没有插头
        LL ans = Hash_map[cur].size?Hash_map[cur].sum[last_status]:0;
        printf("%I64d\n", ans);
    }
}