Eye-in-hand和Eye-to-hand问题求解和实验
2018年12月07日 00:00:40 百川木易 阅读数 3018
2018/12/5 By Yang Yang(yangyang@ipp.ac.cn)
本文所有源码和仿真场景文件全部公开,点击Gitee仓库链接。
文章目录
-
- 问题描述
- Eye-in-hand问题求解公式推导
- Eye-in-hand变换矩阵
- 求解方程
- 仿真实验
- 搭建手眼系统仿真环境
- 生成棋盘图
- 生成仿真棋盘标定板
- 编写手眼系统场景文件
- 编写基于RobWorkStudio的标定图像采集模拟程序
- 编写基于OpenCV的标定计算程序
- 棋盘角点和位姿检测
- 标定计算
- 标定结果比较
- 搭建手眼系统仿真环境
- Eye-to-Hand问题求解公式推导
- Eye-to-Hand变换矩阵
- 求解方程
问题描述
机器人和摄像机的手眼标定问题分为两类构型:
- eye-to-hand,摄像机固定,与机器人基坐标系相对位置不变。
- eye-in-hand,摄像机安装在机器人末端,随着机器人一起移动。
本文主要介绍eye-in-hand构型的标定方法和仿真实验。对于eye-to-hand构型手眼系统,其标定方法与eye-in-hand构型的手眼系统没有本质区别。
Eye-in-hand问题求解公式推导
Eye-in-hand变换矩阵
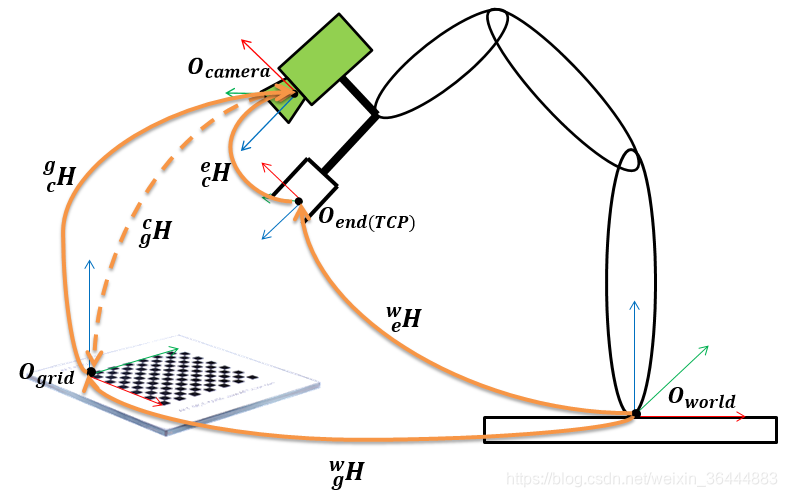
weHi∗ecH=wgH∗gcHi
ewHi∗ceH=gwH∗cgHi
weHj∗ecH=wgH∗gcHj
ewHj∗ceH=gwH∗cgHj
其中:
- weHi
ewHi 和 weHjewHj 表示机器人末端(end)TCP坐标系相对于机器人基座坐标系的齐次变换矩阵,分别对应第 ii 次和第 j
- j 次样本。
- ecH
- ceH 表示摄像机(camera)坐标系相对于机器人末端(end)TCP坐标系的齐次变换矩阵,这是手眼标定问题的求解目标。
- wgH
- gwH 表示棋盘图(grid)相对于世界坐标系(也就是机器人基坐标系)的齐次变换矩阵,由于在整个标定过程中,棋盘图的位置不能变动,因此 wgH
- gwH 是一个常量矩阵。
- gcHi
- cgHi 和 gcHjcgHj 表示摄像机坐标系相对于棋盘图坐标系的齐次变换矩阵。注意:采用OpenCV的solvePnP函数得到的是棋盘图相对于摄像机坐标系的齐次矩阵,即 cgHigcHi 和 cgHj
- gcHj,因此代入以上两个公式时需要进行求逆计算。
BAT=[BAR0ApB01],其逆矩阵为 BAT=[ABRT0−ABRT∗ApB01]齐次变换矩阵求逆方法
对于原齐次矩阵 ABT=[ABR0ApB01]ABT=[BART0−BART∗ApB01]
求解方程
联立上述的两个公式,
weHi∗ecH∗(gcHi)−1=wgH
ewHi∗ceH∗(cgHi)−1=gwH
weHj∗ecH∗(gcHj)−1=wgH
ewHj∗ceH∗(cgHj)−1=gwH
消除常量矩阵 wgH
gwH,
weHi∗ecH∗(gcHi)−1=weHj∗ecH∗(gcHj)−1
ewHi∗ceH∗(cgHi)−1=ewHj∗ceH∗(cgHj)−1
上式两边同时左乘 (weHj)−1
(ewHj)−1 得,
(weHj)−1∗weHi∗ecH∗(gcHi)−1=ecH∗(gcHj)−1
(ewHj)−1∗ewHi∗ceH∗(cgHi)−1=ceH∗(cgHj)−1
上式两边同时右乘 gcHi
cgHi 得
(weHj)−1∗weHi∗ecH=ecH∗(gcHj)−1∗gcHi
(ewHj)−1∗ewHi∗ceH=ceH∗(cgHj)−1∗cgHi
考虑到(gcHj)−1=(cgHj)
(cgHj)−1=(gcHj) 和 (gcHi)=(cgHi)−1(cgHi)=(gcHi)−1,因此上式可以转换为,
(weHj)−1∗weHi∗ecH=ecH∗cgHj∗(cgHi)−1
(ewHj)−1∗ewHi∗ceH=ceH∗gcHj∗(gcHi)−1
令X=ecH
X=ceH,A=(weHj)−1∗weHiA=(ewHj)−1∗ewHi 以及 B=cgHj∗(cgHi)−1B=gcHj∗(gcHi)−1,则上式可以化简为,
AX=XB
AX=XB
以上方程为手眼标定的最终求解方程,具体求解方式可以参考Tasi and Lenz,1989的论文A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration。
仿真实验
以下描述通过仿真实验的方式进行手眼标定测试和验证的方法。大致流程如下:
- 手眼系统仿真场景搭建。
- 标定样本采集。包括摄像机图像采集,以及对应的机器人关节构型采集。
- 图像处理提取棋盘图角点并计算棋盘相对于摄像机坐标系的位姿。
- 采用基于Tasi-lenz的公式进行计算。
仿真实验的主要环境配置和使用到的工具有:
- 操作系统:Windows 7 64bit
- 图像处理工具:Matlab,OpenCV
- 机器人和摄像机仿真环境:RobWork (需先安装QT、Boost等依赖库)
- 虚拟棋盘图编辑:AC3D,用于生成带贴图的棋盘标定板,加载到手眼仿真场景中
搭建手眼系统仿真环境
生成棋盘图
利用如下MATLAB代码"ChessboardGenerator"生成一个边长为30mm,7行10列的棋盘图,图像最终保存为ppm格式的图片文件。之所以选择生成7行10列的棋盘图,是因为这样能够方便的利用OpenCV进行棋盘角点检测,并且保证每张图像的棋盘图坐标系原点都是一致的,角点检测顺序也不会发生改变。不应当使用正方形布置的棋盘图,例如10行10列,这样会导致OpenCV无法统一棋盘原点,给下一步的手眼标定工作带来困难。
以下源码参考用Matlab编写的棋盘格图像生成程序
clc; close all;GridSize = 30; %length of the square m =7; %number of row n = 10; % number of col margin = 10; % white boarder size I = ones(m*GridSize+2*margin,n*GridSize+2*margin)*255;%the first grid is black for i = 1:mif mod(i,2)==1for j = 1:nif mod(j,2)==1I(1+(i-1)*GridSize+margin:i*GridSize+margin,...1+(j-1)*GridSize+margin:j*GridSize+margin) = 0;endendelsefor j = 1:nif mod(j,2)==0I(1+(i-1)*GridSize+margin:i*GridSize+margin,...1+(j-1)*GridSize+margin:j*GridSize+margin) = 0;endendend end imshow(I);imwrite(I,'chessboard.ppm');- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
最终生成棋盘图如下所示。

处理步骤:
- 首先利用ChessboardGenerator生成棋盘图,格式为BMP。棋盘图的长边为10个方块,短边为7个方块,每个方块的尺寸为30个像素单位,另外棋盘图还有10个像素单位的白边。因此整个图像的分辨率为320x230。
- 打开AC3D软件,新建一个Rect矩形,通过MoveTo调整矩形的中心点坐标。
- 通过
 , 调整矩形的尺寸。
, 调整矩形的尺寸。 - 选中矩形对象,在object->Texture设置纹理为步骤(1)中的ppm图像。(图像看起来比较模糊,测试:提高生成图像分辨率,能够获得更清晰的虚拟Chessboard Marker)
- 将矩形保存成chessboard.ac格式文件,必要时用文本编辑器打开该.ac格式文件,如有必要,需修改纹理图像的路径为相对路径。
编写手眼系统场景文件
将上一步生成的chessboard.ac文件添加到场景XML文件中,并且在UR机器人末端设置一个虚拟摄像机,最终得到的机器人运行场景如下图。
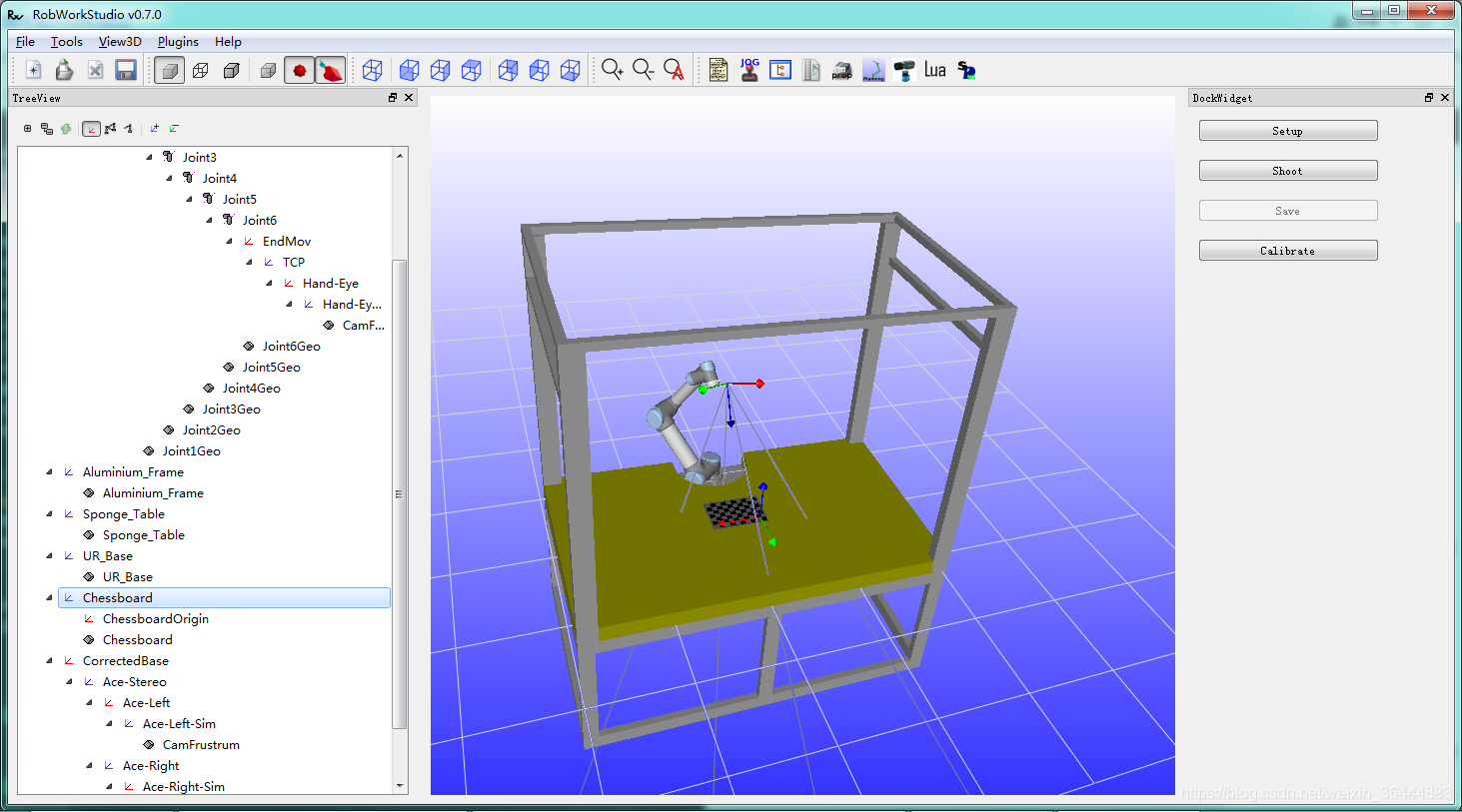
安装在UR末端的摄像机的定义方式可以参考RobWork官网上的教程,本例中摄像机的定义方式如下如下:
<Frame name="Hand-Eye" refframe="UR.TCP"><RPY>0 -15 0</RPY><Pos>0.1 0 0</Pos> </Frame><Frame name="Hand-Eye-Sim" refframe="Hand-Eye" type="Movable"><RPY>0 0 180</RPY><Pos>0 0 0</Pos><Property name="CameraName">Hand-Eye</Property><Property name="Camera">31.0482 960 720</Property> </Frame>- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
编写基于RobWorkStudio的标定图像采集模拟程序
需编写一个RobWorkStudio的插件,用于采集摄像机图片,以及与图像对应的机器人TCP相对于机器人基坐标系的齐次变换矩阵,并保存到本地硬盘上。
源码的运行要求安装RobWork,安装方法参考官网链接。
编译本教程提供源码时,需注意修改加载的机器人场景文件的路径。
编写基于OpenCV的标定计算程序
int cornerRow = 6;int cornerColum = 9;double patternLength = 30.0; //mmvector<rw::math::Transform3D<double> > chessboardPose;vector<Point3d> objectPoints;int pointNumber = cornerRow * cornerColum;for (int i = 0; i < cornerRow; i++){for (int j = 0; j < cornerColum; j++){Point3d p;p.x = patternLength * j;p.y = patternLength * i;p.z = 0;objectPoints.push_back(p);}}int imageResolutionX = 960;int imageResolutionY = 720;double fovy = 31.0482 * 3.14159265 / 180;double focalLength = (imageResolutionY / 2.0) / (tan(fovy / 2.0));Mat cameraMatrix = Mat(3, 3, CV_64FC1, 0.0f);cameraMatrix.at<double>(0, 0) = focalLength;cameraMatrix.at<double>(0, 2) = imageResolutionX / 2.0f;cameraMatrix.at<double>(1, 1) = focalLength;cameraMatrix.at<double>(1, 2) = imageResolutionY / 2.0f;cameraMatrix.at<double>(2, 2) = 1.0f;Mat distortionCoff(0, 0, 0, 0);cout << "\nCamera Matrix: \n" << cameraMatrix << endl;//namedWindow("Display Image", WINDOW_AUTOSIZE);int imageNumber = 25;for (int i = 0; i < imageNumber; i++){char imageName[150];sprintf(imageName, "..\\..\\data\\test-data-01\\image%05d.bmp", i);Mat imageColored = imread(imageName, 1);if (!imageColored.data){printf("No image data \n");return -1;}Mat image;cv::cvtColor(imageColored, image, CV_BGR2GRAY);Size patternSize(cornerColum, cornerRow);vector<Point2f> corners;bool patternfound = findChessboardCorners(image, patternSize, corners, CALIB_CB_ADAPTIVE_THRESH);if (patternfound){printf("found chessboard of image%05d!\n", i);cornerSubPix(image, corners, Size(11, 11), Size(-1, -1), TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));}Mat rvec; //reference to camera frameMat tvec; //reference to camera framesolvePnP(objectPoints, corners, cameraMatrix, distortionCoff, rvec, tvec);Mat chessbaordRotationMatrix; //reference to camera frameRodrigues(rvec, chessbaordRotationMatrix);rw::math::Transform3D<double> t;t(0, 0) = chessbaordRotationMatrix.at<double>(0, 0);t(0, 1) = chessbaordRotationMatrix.at<double>(0, 1);t(0, 2) = chessbaordRotationMatrix.at<double>(0, 2);t(0, 3) = tvec.at<double>(0) / 1000; //mm to mt(1, 0) = chessbaordRotationMatrix.at<double>(1, 0);t(1, 1) = chessbaordRotationMatrix.at<double>(1, 1);t(1, 2) = chessbaordRotationMatrix.at<double>(1, 2);t(1, 3) = tvec.at<double>(1) / 1000; //mm to mt(2, 0) = chessbaordRotationMatrix.at<double>(2, 0);t(2, 1) = chessbaordRotationMatrix.at<double>(2, 1);t(2, 2) = chessbaordRotationMatrix.at<double>(2, 2);t(2, 3) = tvec.at<double>(2) / 1000; //mm to m//printTransformation(t);chessboardPose.push_back(t);}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
其中一张棋盘图的角点检测结果如下图:

标定计算
标定计算程序主要参考了经典手眼标定算法之Tsai-Lenz的OpenCV实现,主要源码如下:
cv::Mat skew(cv::Mat m) {Mat t(3, 3, CV_64FC1);t.at<double>(0, 0) = 0;t.at<double>(0, 1) = - m.at<double>(2, 0);t.at<double>(0, 2) = m.at<double>(1, 0);t.at<double>(1, 0) = m.at<double>(2, 0);t.at<double>(1, 1) = 0;t.at<double>(1, 2) = - m.at<double>(0, 0);t.at<double>(2, 0) = - m.at<double>(1, 0);t.at<double>(2, 1) = m.at<double>(0, 0);t.at<double>(2, 2) = 0;return t; }void Tsai_HandEye(Mat Hcg, vector<Mat> Hgij, vector<Mat> Hcij) {CV_Assert(Hgij.size() == Hcij.size());int nStatus = Hgij.size();Mat Rgij(3, 3, CV_64FC1);Mat Rcij(3, 3, CV_64FC1);Mat rgij(3, 1, CV_64FC1);Mat rcij(3, 1, CV_64FC1);double theta_gij;double theta_cij;Mat rngij(3, 1, CV_64FC1);Mat rncij(3, 1, CV_64FC1);Mat Pgij(3, 1, CV_64FC1);Mat Pcij(3, 1, CV_64FC1);Mat tempA(3, 3, CV_64FC1);Mat tempb(3, 1, CV_64FC1);Mat A;Mat b;Mat pinA;Mat Pcg_prime(3, 1, CV_64FC1);Mat Pcg(3, 1, CV_64FC1);Mat PcgTrs(1, 3, CV_64FC1);Mat Rcg(3, 3, CV_64FC1);Mat eyeM = Mat::eye(3, 3, CV_64FC1);Mat Tgij(3, 1, CV_64FC1);Mat Tcij(3, 1, CV_64FC1);Mat tempAA(3, 3, CV_64FC1);Mat tempbb(3, 1, CV_64FC1);Mat AA;Mat bb;Mat pinAA;Mat Tcg(3, 1, CV_64FC1);for (int i = 0; i < nStatus; i++){Hgij[i](Rect(0, 0, 3, 3)).copyTo(Rgij);Hcij[i](Rect(0, 0, 3, 3)).copyTo(Rcij);Rodrigues(Rgij, rgij);Rodrigues(Rcij, rcij);theta_gij = norm(rgij);theta_cij = norm(rcij);rngij = rgij / theta_gij;rncij = rcij / theta_cij;Pgij = 2 * sin(theta_gij / 2)*rngij;Pcij = 2 * sin(theta_cij / 2)*rncij;tempA = skew(Pgij + Pcij);tempb = Pcij - Pgij;A.push_back(tempA);b.push_back(tempb);}//Compute rotationinvert(A, pinA, DECOMP_SVD);Pcg_prime = pinA * b;Pcg = 2 * Pcg_prime / sqrt(1 + norm(Pcg_prime) * norm(Pcg_prime));PcgTrs = Pcg.t();Rcg = (1 - norm(Pcg) * norm(Pcg) / 2) * eyeM + 0.5 * (Pcg * PcgTrs + sqrt(4 - norm(Pcg)*norm(Pcg))*skew(Pcg));//Computer Translation for (int i = 0; i < nStatus; i++){Hgij[i](Rect(0, 0, 3, 3)).copyTo(Rgij);Hcij[i](Rect(0, 0, 3, 3)).copyTo(Rcij);Hgij[i](Rect(3, 0, 1, 3)).copyTo(Tgij);Hcij[i](Rect(3, 0, 1, 3)).copyTo(Tcij);tempAA = Rgij - eyeM;tempbb = Rcg * Tcij - Tgij;AA.push_back(tempAA);bb.push_back(tempbb);}invert(AA, pinAA, DECOMP_SVD);Tcg = pinAA * bb;Rcg.copyTo(Hcg(Rect(0, 0, 3, 3)));Tcg.copyTo(Hcg(Rect(3, 0, 1, 3)));Hcg.at<double>(3, 0) = 0.0;Hcg.at<double>(3, 1) = 0.0;Hcg.at<double>(3, 2) = 0.0;Hcg.at<double>(3, 3) = 1.0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
标定结果比较
在自定义的手眼标定场景文件中,摄像机相对于机器人TCP的关系如下:
<Frame name="Hand-Eye" refframe="UR.TCP"><RPY>0 -15 0</RPY><Pos>0.1 0 0</Pos> </Frame>- 1
- 2
- 3
- 4
转换成4 ×
× 4的齐次变换矩阵如下:
ecH=⎡⎣⎢⎢⎢⎢0.96592600.25881900100−0.25881900.96592600.1001⎤⎦⎥⎥⎥⎥
ceH=⎣⎢⎢⎡0.96592600.25881900100−0.25881900.96592600.1001⎦⎥⎥⎤
通过Tasi-Lenz方法计算得出的(不考虑摄像机参数误差)摄像机相对于机器人TCP的关系如下:
ecH=⎡⎣⎢⎢⎢⎢0.9659861360843613−0.00031871107048437940.258593664493272700.00038437325583683220.9999999054504882−0.00020336227483621180−0.25859357522955960.00029584162685441490.965986167254855500.10012491158556857.92132967571962e−053.021520822331239e−051⎤⎦⎥⎥⎥⎥ceH=⎣⎢⎢⎡0.9659861360843613−0.00031871107048437940.258593664493272700.00038437325583683220.9999999054504882−0.00020336227483621180−0.25859357522955960.00029584162685441490.965986167254855500.10012491158556857.92132967571962e−053.021520822331239e−051⎦⎥⎥⎤
通过对比以上两组齐次变换矩阵结果,可以两者是十分接近的,证明手眼标定结果是正确的。Eye-to-Hand问题求解公式推导
Eye-to-Hand变换矩阵
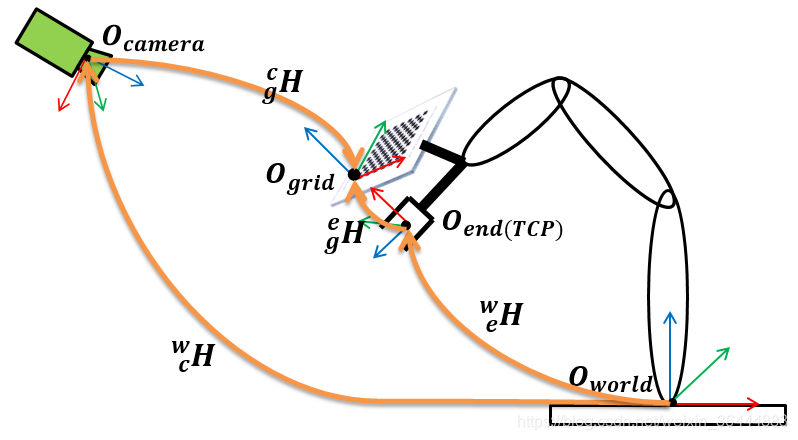
wcH∗cgHi=weHi∗egH
cwH∗gcHi=ewHi∗geH
wcH∗cgHj=weHj∗egHcwH∗gcHj=ewHj∗geH
其中:- wcH
- cwH表示摄像机(camera)坐标系相对于机器人基坐标系(也是世界坐标,world)的齐次变换矩阵。这是Eye-to-hand问题的求解目标。
- cgHi
- gcHi和cgHigcHi表示棋盘图(grid)相对于摄像机坐标系的齐次变换矩阵,分别对应第 ii 次和第 j
- j 次样本。
- weHi
- ewHi 和 weHjewHj 表示机器人末端(end)TCP坐标系相对于机器人基座坐标系的齐次变换矩阵,分别对应第 ii 次和第 j
- j 次样本。
- egH
- geH 表示棋盘图(grid)相对于机器人末端TCP的齐次变换矩阵,由于在整个标定过程中,棋盘图固定连接在机器人末端,因此 egH
- geH 是一个常量矩阵。
求解方程
改写以上公式:
(ewHi)−1∗cwH∗gcHi=geH
(weHi)−1∗wcH∗cgHi=egH
(weHj)−1∗wcH∗cgHj=egH(ewHj)−1∗cwH∗gcHj=geH
消除常量egHgeH,
(weHi)−1∗wcH∗cgHi=(weHj)−1∗wcH∗cgHj(ewHi)−1∗cwH∗gcHi=(ewHj)−1∗cwH∗gcHj
上式两边同时左乘weHjewHj得,
weHj∗(weHi)−1∗wcH∗cgHi=wcH∗cgHjewHj∗(ewHi)−1∗cwH∗gcHi=cwH∗gcHj
上式两边同时右乘(cgHi)−1(gcHi)−1,
weHj∗(weHi)−1∗wcH=wcH∗cgHj∗(cgHi)−1ewHj∗(ewHi)−1∗cwH=cwH∗gcHj∗(gcHi)−1
令X=wcHX=cwH,A=weHj∗(weHi)−1A=ewHj∗(ewHi)−1,B=cgHj∗(cgHi)−1B=gcHj∗(gcHi)−1,可得
AX=XBAX=XB
以上方程是Eye-to-Hand标定的最终求解方程,具体求解方式可以参考Tasi and Lenz,1989的论文A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration。具体的eye-to-hand求解仿真可以参考eye-in-hand标定求解仿真进行,这里不再赘述
















![Java基础教程:面向对象编程[2]](http://pic.xiahunao.cn/Java基础教程:面向对象编程[2])

全过程)
