【codeforces】【比赛题解】#849 CF Round #431 (Div.2)

cf的比赛越来越有难度了……至少我做起来是这样。

先看看题目吧：点我。

这次比赛是北京时间21:35开始的，算是比较良心。

【A】奇数与结束

"奇数从哪里开始，又在哪里结束？梦想从何处起航，它们又是否会破灭呢？"

给定一个长度为n的序列。确定能不能将序列分成奇数个长度为奇数的非空字串，而且这其中每个子串以奇数开头，以奇数结尾。可以只分成一个（1也是奇数）。

输入

第一行一个正整数n，表示序列长度。

第二行n个整数，表示序列中的元素。

输出

输出"Yes"或"No"来表示能否做到把序列按要求分割。

样例输入1

5
1 0 1 5 1

样例输出1

Yes

样例输入2

4
3 9 9 3

样例输出2

题解

当时想了一个n²的DP，之后发现实在是太naive。

讲一下DP思路吧，用f1[i]表示能否将a[1...i]分割成奇数个奇数长度的子串，并且每个子串以奇数开头结尾，f2[i]表示能否分割成偶数个子串。

于是f1[i]=OR(f2[j] (a[j+1...i]长度为奇数并且以奇数开头结尾) )，f2[i]=OR(f1[j] (a[j+1...i]长度为奇数并且以奇数开头结尾) ).

特别的，f1[0]=false，f2[0]=true。

这种做法就可以过了，但是有更优秀的做法：

把序列分成奇数个奇数长度的序列，那么这个序列也是奇数长度的。偶数长度的直接No。

再考虑把序列分成两个以上的序列，那么最开始的序列的起始元素必须是奇数，最末尾的序列的结尾元素也必须是奇数。

这就对应了原序列的第一个与最后一个元素必须是奇数，而这时我们只分一段就好了。

就是说我们只需要判断n的奇偶，a[1]的奇偶和a[n]的奇偶就可以了。

程序：

 1 #include <cstdio>
 2 static const int MAXN = 102;
 3 
 4 int n;
 5 int a[MAXN];
 6 
 7 int main()
 8 {
 9     scanf("%d", &n);
10     for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
11 
12     puts((n & 1) && (a[0] & 1) && (a[n - 1] & 1) ? "Yes" : "No");
13     return 0;
14 }

【B】

目前没做出来，调出来了再说自己的做法吧

先贴标程：

 1 #include <bits/stdc++.h>
 2 #define eps 1e-7
 3 using namespace std;
 4 int read()
 5 {
 6     int x=0,f=1;char ch=getchar();
 7     while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
 8     while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
 9     return x*f;
10 }
11 int n,a[1007];
12 bool vis[1007];
13 bool check(double k,int b)
14 {
15     memset(vis,false,sizeof(vis));
16     int cnt=0;
17     for (int i=1;i<=n;i++)
18     {
19         if (a[i]-b==1LL*k*(i-1)) 
20         {
21             vis[i]=true;
22             ++cnt;
23         }
24     }
25     if (cnt==n) return false;
26     if (cnt==n-1) return true;
27     int pos1=0;
28     for (int i=1;i<=n;i++)
29         if (!vis[i]&&pos1==0) pos1=i;
30     for (int i=pos1+1;i<=n;i++)
31         if (!vis[i])
32         {
33             if (fabs((double)(a[i]-a[pos1])/(i-pos1)-k)>eps) return false;
34         }
35     return true;
36 }
37 int main()
38 {
39     n=read();
40     for (int i=1;i<=n;i++)
41         a[i]=read();
42     bool ans=false;
43     ans|=check(1.0*(a[2]-a[1]),a[1]);
44     ans|=check(0.5*(a[3]-a[1]),a[1]);
45     ans|=check(1.0*(a[3]-a[2]),a[2]*2-a[3]);
46     if (ans) printf("Yes\n"); else printf("No\n");
47     return 0;
48 }

【C】

题目都没看懂，真的很难受，这题挺难的。

标程：

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 using ll = long long;
 6 using ld = long double;
 7 using D = double;
 8 using uint = unsigned int;
 9 template<typename T>
10 using pair2 = pair<T, T>;
11 
12 #ifdef WIN32
13     #define LLD "%I64d"
14 #else
15     #define LLD "%lld"
16 #endif
17 
18 #define pb push_back
19 #define mp make_pair
20 #define all(x) (x).begin(),(x).end()
21 #define fi first
22 #define se second
23 
24 int main()
25 {
26     int k;
27     scanf("%d", &k);
28     for (int i = 0; i < 26; i++)
29     {
30         int cnt = 1;
31         while ((cnt + 1) * cnt / 2 <= k) cnt++;
32         k -= cnt * (cnt - 1) / 2;
33         for (int j = 0; j < cnt; j++) printf("%c", 'a' + i);
34     }
35     return 0;
36 }

【D】Rooter's Song

"无论目标何在，无论遇见何人，让我们一同将这首歌传唱。"

在平面直角坐标系中，有一个长方形舞台，四角分别是(0,0)，(0,h)，(w,0)，(w,h)。

可以看出在有任何人进入舞台之前，不会有任何碰撞发生。

在舞台的左边界和下边界站着一些舞者。分成两组：

①竖直：站在(xi,0)上，沿着y正方向前进（向上）。

②水平：站在(0,yi)上，沿着x正方向前进（向右）。

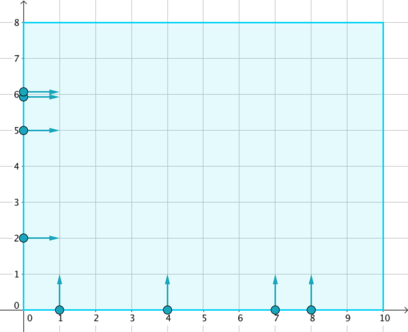
按照编舞指导，第i个舞者需要在前ti毫秒内站着不动，然后沿着指定方向以1单位/毫秒的速度前进，直到碰到舞台的边界为止。

当两个舞者碰撞时，她们会立刻改变各自的前进方向，然后继续沿着新的方向前进。

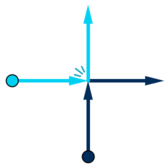
舞者们只要碰到了舞台的边界就会停止，请求出每个舞者最终停下的位置。

输入

第一行有三个数n,w,h。表示舞者数量，舞台的长宽。

接下来n行，每行三个数，gi,pi,ti，表示第i个舞者所在的组（gi=1：竖直组；gi=2：水平组），坐标位置（gi=1则pi=xi；gi=2则pi=yi）以及等待时间。

保证0<xi<w，0<yi<h。并保证没有两个舞者既在相同的组，还有相同的位置和等待时间。

输出

n行，每行两个数xi,yi。表示第i个舞者最终停在哪里。

样例输入1

8 10 8
1 1 10
1 4 13
1 7 1
1 8 2
2 2 0
2 5 14
2 6 0
2 6 1

样例输出1

4 8
10 5
8 8
10 6
10 2
1 8
7 8
10 6

样例输入2

3 2 3
1 1 2
2 1 1
1 1 5

样例输出2

1 3
2 1
1 3

数据范围及提示

1<=n<=100000，2<=w,h<=100000，1<=gi<=2，1<=pi<=99999，0<=ti<=100000。

对于样例数据1，这是对应的图：

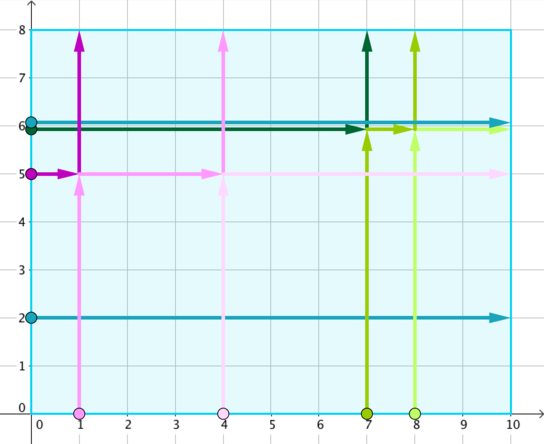
对于样例数据2，没有舞者碰撞。

题解

很难的一题，不过我看来比C题简单……

注意到每个舞者出发后，每毫秒其坐标总是有一个加一，故(xi+yi)总是在增加。

而且我们发现，只有(xi+yi)相同的舞者才会碰撞。我们把(xi+yi)的值相同的舞者分在一起处理。

如何确定(xi+yi)的值呢？？可以发现对于每个舞者，可以把(pi-ti)近似看做(xi+yi)，(pi-ti)相同的舞者可能碰撞，而(pi-ti)不同的不可能碰撞。

我们对舞者按照(pi-ti)排序，处理出(pi-ti)相同的舞者。

对于(pi-ti)相同的舞者，我们如何处理呢？

试着把舞台斜过来看吧！让(0,0)在最下方，(w,h)在最顶端，(0,h)在左侧，(w,0)在最右侧。

这样，对于那些(pi-ti)相同的舞者，即出发后(xi+yi)相同的舞者们，她们在同一时间点必然处在同一水平线上。

并且每过一毫秒，她们向上走√2/2单位，向左或向右走√2/2单位。

这时候的碰撞要如何处理呢？

注意到在没有碰撞发生前，舞者从左到右的顺序是先是水平方向的舞者，坐标从大到小下来，然后是竖直方向的舞者，坐标从小到大往右走。

而所有碰撞都发生了之后呢？？舞者的相对位置是不会改变的！原本在最左侧的舞者，仍然在左侧。舞者位置不会交换。

或者……这是另一种形式的交换了呢？注意到在水平方向坐标最大的舞者没有去到她本来应该去的位置，而是去了竖直方向第一个舞者应该去的位置。

是的，她们的位置交换了，但是这种交换很有规律，把舞者分成水平方向和竖直方向，那么水平方向的舞者按顺序要去到竖直方向的舞者按顺序应该去到的位置。依次推下来，就可以确定舞者最终的位置。我不太好解释这种方法的具体实现，先贴代码吧。

排序时要注意第一关键字是(pi-ti)，第二关键字是先水平，后竖直，第三关键字是初始坐标，水平的从大到小，竖直的从小到大。

复杂度O(nlogn)

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<cstring>
 4 #define F(i,a,b) for(int i=a;i<=b;++i)
 5 #define F2(i,a,b) for(int i=a;i<b;++i)
 6 int n,w,h,g[100002],p[100002],t[100002],I[100002],Ans[100002],Ansg[100002];
 7 inline bool cmp(int x,int y){
 8     if(p[x]-t[x]<p[y]-t[y]) return 1;
 9     else if(p[x]-t[x]>p[y]-t[y]) return 0;
10     else{
11         if(g[x]>g[y]) return 1;
12         else if(g[x]<g[y]) return 0;
13         else{
14             if(g[x]==1) return p[x]<p[y];
15             else return p[x]>p[y];
16         }
17     }
18 }
19 int main(){
20     scanf("%d%d%d",&n,&w,&h);
21     F(i,1,n) scanf("%d%d%d",g+i,p+i,t+i),I[i]=i;
22     std::sort(I+1,I+n+1,cmp);
23     I[n+1]=0; p[0]=99999999; t[0]=-99999999;
24     int hor=0,ver=0;
25     F(i,1,n){
26         if(g[I[i]]==1) ++ver; else ++hor;
27         if(p[I[i]]-t[I[i]]!=p[I[i+1]]-t[I[i+1]]){
28             int j=i-hor-ver+1, k=i-ver+1,l,o;
29             for(l=k,o=j;l<=i;++l,++o)
30                 Ans[I[o]]=p[I[l]],Ansg[I[o]]=g[I[l]];
31             for(;o<=i;++o,++j)
32                 Ans[I[o]]=p[I[j]],Ansg[I[o]]=g[I[j]];
33             ver=hor=0;
34         }
35     }
36     F(i,1,n) if(Ansg[i]==1) printf("%d %d\n",Ans[i],h); else printf("%d %d\n",w,Ans[i]);
37     return 0;
38 }