POJ 1811 Prime Test （Rabin-Miller强伪素数测试 和Pollard-rho 因数分解）

题目链接

Description

Given a big integer number, you are required to find out whether it's a prime number.

Input

The first line contains the number of test cases T (1 <= T <= 20 ), then the following T lines each contains an integer number N (2 <= N < 254).

Output

For each test case, if N is a prime number, output a line containing the word "Prime", otherwise, output a line containing the smallest prime factor of N.

Sample Input

2
5
10

Sample Output

Prime
2

分析：
给定一个小于2^54的整数，判断该数是不是素数，如果是素数的话，输出“Prime”，否则输出该数的最小的素因子。熟悉的有关素数的算法在这道题看来都还是太弱了，所以得额外的找方法来解决。

应用到的两个重要算法是Rabin-Miller强伪素数测试和Pollard 因数分解算法。前者可以在 的时间内以很高的成功概率判断一个整数是否是素数。后者可以在最优 的时间内完成合数的因数分解。这两种算法相对于试除法都显得比较复杂。本文试图对这两者进行简单的阐述，说明它们在32位计算机上限制在64位以内的条件下的实现中的细节。下文提到的所有字母均表示整数。

一、Rabin-Miller强伪素数测试
Rabin-Miller强伪素数测试的基本思想来源于如下的Fermat小定理：
如果p是一个素数，则对任意a有 (a^p)%p=a。特别的，如果p不能整除a，则还有(a^(p-1))%p=1 。
利用Fermat小定理可以得到一个测试合数的有力算法：对n>1，选择a>1，计算(a^(n-1))%n，若结果不等于1则n是合数。若结果等于1则n可能是素数，并被称为一个以a为基的弱可能素数（weak probable prime base a，a-PRP）;若n是合数，则又被称为一个以a为基的伪素数（pseudoprime）。

这个算法的成功率是相当高的。在小于25,000,000,000的1,091,987,405个素数中，一共只用21,853个以2为基的伪素数。但不幸的是，Alford、Granville和Pomerance在1994年证明了存在无穷多个被称为Carmichael数的整数对于任意与其互素的整数a算法的计算结果都是1。最小的五个Carmichael数是561、1,105、1,729、2,465和2,801。

考虑素数的这样一个性质：若n是素数，则1对模n的平方根只可能是1和-1 。因此a^(n-1) 对模n的平方根 a^((n-1)/2)也只可能是1和-1 。如果(n-1)/2本身还是一个偶数，我们可以再取一次平方根……将这些写成一个算法：
（Rabin-Miller强伪素数测试）记n-1=(2^s)d，其中d是奇数而s非负。如果(a^d)%n=1 ，或者对某个 0<=r<s有(a^((2^r)d))%n=-1 ，则认为n通过测试，并称之为一个以a为基的强可能素数（strong probable prime base a，a-SPRP）。若n是合数，则又称之为一个以a为基的强伪素数（strong pseudoprime）。

这个测试同时被冠以Miller的名字是因为Miller提出并证明了如下测试：如果扩展黎曼猜想（extended Riemann hypothesis）成立，那么对于所有满足1<a<2(log n)^2 的基a，n都是a-SPRP，则n是素数。
尽管Monier和Rabin在1980年证明了这个测试的错误概率（即合数通过测试的概率）不超过 1/4，单个测试相对来说还是相当弱的（Pomerance、Selfridge和Wagstaff, Jr.证明了对任意a>1都存在无穷多个a-SPRP）。但由于不存在“强Carmichael数”（任何合数n都存在一个基a试之不是a-SPRP），我们可以组合多个测试来产生有力的测试，以至于对足够小的n可以用来证明其是否素数。

取前k个素数为基，并用 来表示以前k个素数为基的强伪素数，Riesel在1994年给出下表：

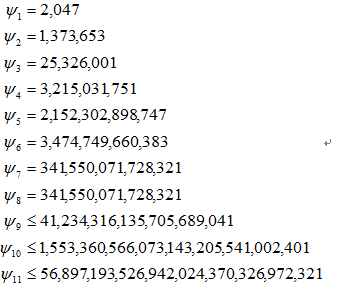
考虑到64位二进制数能表示的范围，只需取前9个素数为基，则对小于φ8 的所有大于1的整数测试都是正确的；对大于或等于 φ8并小于2^64 的整数测试错误的概率不超过1/(2^18) 。

Rabin-Miller强伪素数测试本身的形式稍有一些复杂，在实现时可以下面的简单形式代替：
对 n>1，如果(a^(n-1))%n=1则认为n通过测试。
代替的理由可简单证明如下：
仍然记n-1=(2^s)d ，其中d是奇数而s非负。若n是素数，由(a^(n-1))%n=1可以推出(a^(2^(s-1)d))%n=1=(a^((n-1)/2))%n或(a^(2^(s-1)d))%n=-1=(a^((n-1)/2))%n 。若为前者，显然取r=s-1 即可使n通过测试。若为后者，则继续取平方根，直到对某个 1<=r<s有 (a^((2^r)d))%n=-1，或(a^(2d))%n=1 。无论 (a^d)%n=1还是 a^d)%n=-1，n都通过测试。

Rabin-Miller强伪素数测试的核心是幂取模（即计算 ）(a^s)%n。计算幂取模有以下的 O(log n)算法（以Sprache伪代码语言描述）：
这个算法在32位计算机上实现的难点在于指令集和绝大部分编程语言的编译器都只提供了32位相乘结果为64位的整数乘法，浮点运算由于精度的问题不能应用于这里的乘法。唯一解决办法是模仿一些编译器内建的64位整数乘法来实现两个无符号64位相乘结果为128位的乘法。这个乘法可以将两个乘数分别分割成两个32位数来实现。为方便乘法之后的取模运算，运算结果应当用连续的128个二进制位来表示。以下是其伪代码：

乘法之后的取模运算可以用浮点运算快速完成。具体做法是乘积的高64位和低64位分别先对除数取模，然后再利用浮点单元合并取模。这里的浮点运算要求浮点单元以最高精度运算，计算前应先将浮点单元控制字中的精度控制位设置为64位精度。为保证精度，应当用80位浮点数实现此运算。伪代码如下：

至此，Rabin-Miller强伪素数测试的核心已经全部实现。

二、Pollard-rho 因数分解算法
Pollard-rho因数分解算法又称为Pollard Monte Carlo因数分解算法。它的核心思想是：选取一个随机数a。再选一个随机数b。检查 gcd(a-b,n)是否大于1。若大于1， gcd(a-b,n)就是n的一个因子。若不大于1，再选取随机数c，检查 gcd(c-b,n)和 gcd(c-a,n)。如此继续，直到找到n的一个非平凡因子。

代码：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <time.h>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll __int64//****************************************************************
// Miller_Rabin 算法进行素数测试
//速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=20;//随机算法判定次数，S越大，判错概率越小//计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
/*
ll Mult_mod (ll a,ll b,ll c)   //  a,b,c <2^63
{a%=c;b%=c;ll ret=0;while (b){if (b&1) {ret+=a;ret%=c;}a<<=1;if (a>=c)a%=c;b>>=1;}return ret;
}*/ll Mult_mod (ll a,ll b,ll c)  //减法实现比取模速度快
{//返回(a*b) mod c,a,b,c<2^63a%=c;b%=c;ll ret=0;while (b){if (b&1){ret+=a;if (ret>=c) ret-=c;}a<<=1;if (a>=c) a-=c;b>>=1;}return ret;
}//计算  x^n %c
ll Pow_mod (ll x,ll n,ll mod) //x^n%c
{if (n==1) return x%mod;x%=mod;ll tmp=x;ll ret=1;while (n){if (n&1) ret=Mult_mod(ret,tmp,mod);//(a*b)%ctmp=Mult_mod(tmp,tmp,mod);n>>=1;}return ret;
}//以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
//一定是合数返回true,不一定返回false
bool Check (ll a,ll n,ll x,ll t)
{ll ret=Pow_mod(a,x,n);//(a^x)%nll last=ret;for (int i=1; i<=t; i++){ret=Mult_mod(ret,ret,n);if(ret==1&&last!=1&&last!=n-1) return true; //合数last=ret;}if (ret!=1) return true;return false;
}// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数，但概率极小)
//合数返回false;bool Miller_Rabin (ll n)
{if (n<2) return false;if (n==2) return true;if ((n&1)==0) return false;//偶数ll x=n-1;ll t=0;while ((x&1)==0)//不断的对于x进行右移操作{x>>=1;t++;}for (int i=0; i<S; i++){ll a=rand()%(n-1)+1; //rand()需要stdlib.h头文件if (Check(a,n,x,t))return false;//合数}return true;
}//************************************************
//pollard_rho 算法进行质因数分解
//************************************************ll factor[100];//质因数分解结果（刚返回时是无序的）
int tol;//质因数的个数。数组下标从0开始ll Gcd (ll a,ll b)
{if (a==0) return 1;   if (a<0) return Gcd(-a,b);while (b){ll t=a%b;a=b;b=t;}return a;
}ll Pollard_rho (ll x,ll c)
{ll i=1,k=2;ll x0=rand()%x;ll y=x0;while (true){i++;x0=(Mult_mod(x0,x0,x)+c)%x;ll d=Gcd(y-x0,x);if (d!=1 && d!=x) return d;if (y==x0) return x;if (i==k){y=x0;k+=k;}}
}
//对n进行素因子分解
void Findfac (ll n)
{if (Miller_Rabin(n)) //素数{factor[tol++]=n;return;}ll p=n;while (p>=n) p=Pollard_rho(p,rand()%(n-1)+1);Findfac(p);Findfac(n/p);
}int main ()  // Poj 1811 交G++ 比c++ 快很多
{// srand(time(NULL));//需要time.h头文件  //POJ上G++要去掉这句话int T;scanf("%d",&T);while (T--){ll n;scanf("%I64d",&n);if (Miller_Rabin(n)){printf("Prime\n");continue;}tol=0;Findfac(n);ll ans=factor[0];for (int i=1; i<tol; i++)if (factor[i]<ans)ans=factor[i];printf("%I64d\n",ans);}return 0;
}