转载自：https://blog.csdn.net/bone_ace/article/details/46239187

凸包问题的五种解法

2015年05月29日 17:58:51

阅读数：33660

前言：

首先，什么是凸包？
假设平面上有p0~p12共13个点，过某些点作一个多边形，使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候，我们就叫它“凸包”。如下图：
这里写图片描述

然后，什么是凸包问题？
我们把这些点放在二维坐标系里面，那么每个点都能用 (x,y) 来表示。
现给出点的数目13，和各个点的坐标。求构成凸包的点？

解一：穷举法（蛮力法）

时间复杂度：O(n³）。
思路：两点确定一条直线，如果剩余的其它点都在这条直线的同一侧，则这两个点是凸包上的点，否则就不是。
步骤：

将点集里面的所有点两两配对，组成 n(n-1)/2 条直线。
对于每条直线，再检查剩余的 (n-2) 个点是否在直线的同一侧。

如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢？（坐标：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）

这里写图片描述
当上式结果为正时，p3在直线 p1p2 的左侧；当结果为负时，p3在直线 p1p2 的右边。

解二：分治法

时间复杂度：O(n㏒n)。
思路：应用分治法思想，把一个大问题分成几个结构相同的子问题，把子问题再分成几个更小的子问题……。然后我们就能用递归的方法，分别求这些子问题的解。最后把每个子问题的解“组装”成原来大问题的解。
步骤：

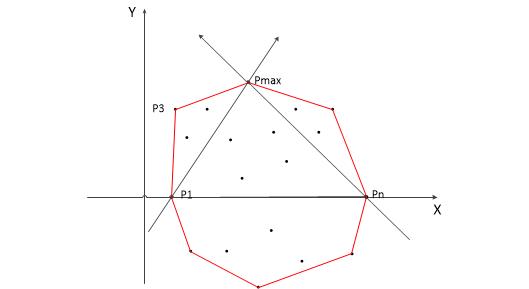
把所有的点都放在二维坐标系里面。那么横坐标最小和最大的两个点 P1 和 Pn 一定是凸包上的点（为什么呢？用反证法很容易证明，这里不详讲）。直线 P1Pn 把点集分成了两部分，即 X 轴上面和下面两部分，分别叫做上包和下包。
对上包：求距离直线 P1Pn 最远的点，即下图中的点 Pmax 。
作直线 P1Pmax 、PnPmax，把直线 P1Pmax 左侧的点当成是上包，把直线 PnPmax 右侧的点也当成是上包。
重复步骤 2、3。
对下包也作类似操作。

这里写图片描述

然而怎么求距离某直线最远的点呢？我们还是用到解一中的公式：
这里写图片描述
设有一个点 P3 和直线 P1P2 。（坐标：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）
对上式的结果取绝对值，绝对值越大，则距离直线越远。

注意：在步骤一，如果横坐标最小的点不止一个，那么这几个点都是凸包上的点，此时上包和下包的划分就有点不同了，需要注意。

解三：Jarvis步进法

时间复杂度：O(nH)。（其中 n 是点的总个数，H 是凸包上的点的个数）
思路：

纵坐标最小的那个点一定是凸包上的点，例如图上的 P0。
从 P0 开始，按逆时针的方向，逐个找凸包上的点，每前进一步找到一个点，所以叫作步进法。
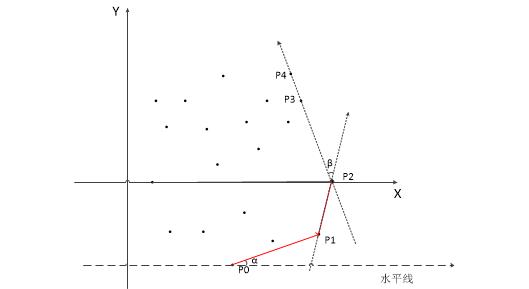
怎么找下一个点呢？利用夹角。假设现在已经找到 {P0，P1，P2} 了，要找下一个点：剩下的点分别和 P2 组成向量，设这个向量与向量P1P2的夹角为 β 。当 β 最小时就是所要求的下一个点了，此处为 P3 。

这里写图片描述

注意：

找第二个点 P1 时，因为已经找到的只有 P0 一个点，所以向量只能和水平线作夹角 α，当 α 最小时求得第二个点。
共线情况：如果直线 P2P3 上还有一个点 P4，即三个点共线，此时由向量P2P3 和向量P2P4 产生的两个 β 是相同的。我们应该把 P3、P4 都当做凸包上的点，并且把距离 P2 最远的那个点（即图中的P4）作为最后搜索到的点，继续找它的下一个连接点。

解四：Graham扫描法

时间复杂度：O(n㏒n)
思路：Graham扫描的思想和Jarris步进法类似，也是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，但它不是利用夹角。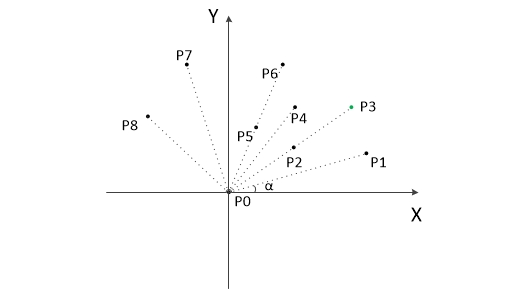
这里写图片描述
步骤：

把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
把所有点的坐标平移一下，使 P0 作为原点，如上图。
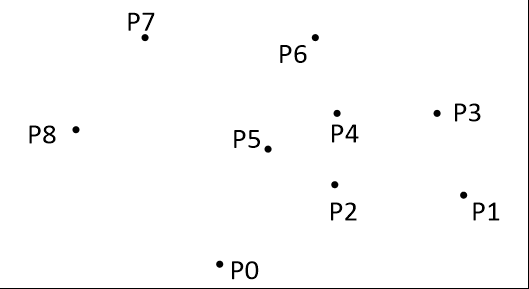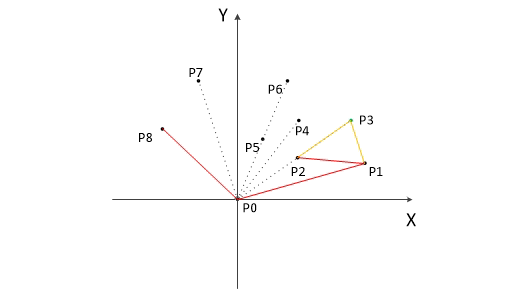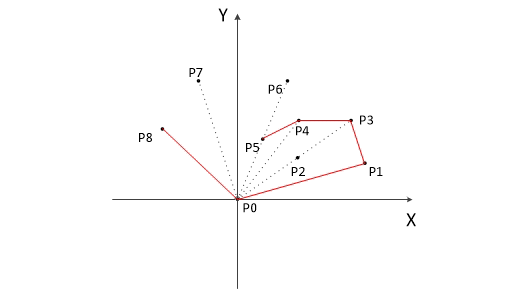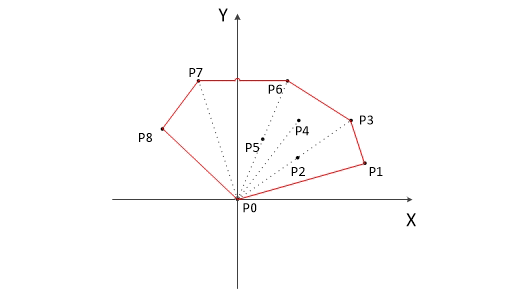
计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
（以上是准备步骤，以下开始求凸包）
以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：
连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
当前点是凸包上的点，把它压入栈，执行步骤7。
检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

最后，栈中的元素就是凸包上的点了。
以下为用Graham扫描法动态求解的过程：
这里写图片描述

代码：poj1873

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#define zero(a) (fabs((double)(a))<(1e-8))
using namespace std;
const int eps=1e-8;
struct tr{int x,y,v,l;
}s1[20],s[20];
int st[20];
int mul(tr p,tr u,tr v){//求叉积 return (p.x-u.x)*(v.y-u.y)-(v.x-u.x)*(p.y-u.y);
}
double dis(tr a,tr b){//求长度 return sqrt((double)(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp(tr a,tr b){//极角排序 if(mul(a,s[0],b)>0)//以最小点s[0]为基准排序 return true;else if(zero(mul(a,s[0],b))&&dis(s[0],a)<dis(s[0],b))return true;return false;
}
int mv,ct,nt;
double l2;
int do1(int n,int l1,int mv1,int c){int i,j;int x,y;double l;//要用的木材长度 if(n==1){l=0;}/*else if(n==2){l=dis(s[0],s[1])*2;}*/ else{ l=0;for(i=1;i<n;i++){if(s[0].y>s[i].y||(s[0].y==s[i].y&&s[0].x>s[i].x)){//将s[0]化为最小点，以便极角排序 swap(s[0],s[i]);}}sort(s+1,s+n,cmp);//排序 int top,cnt;st[0]=0;st[1]=1;tr a,b;top=2;cnt=2;while(cnt<n-1){//当 st[top]=cnt;//先放入当前点 top++;cnt++;a=s[st[top-1]];b=s[st[top-2]];while(mul(s[cnt],a,b)<eps){//以当前点的下一个点为标杆点来除去不合凸包条件的点（Graham扫描法）（如果标杆点在当前栈顶的两个点组成的直线的右边，则说明栈顶的点不是凸包上的点） top--;//去掉不合条件的点 a=b;//重新判断当前栈顶的点 b=s[st[top-2]];}}st[top++]=n-1;//压入最后一次的标杆点，它一定是凸包上的点，因为它在最左边 for( i=0;i<top-1;i++){l+=dis(s[st[i]],s[st[i+1]]);}l+=dis(s[0],s[n-1]);//把这句代码写成了l+=dis(s[st[0]],s[st[n-1]]),卡了三个小时，QAQ，引以为戒啊 }//printf("%d %d\n",l1,l);if((l1-l)>=0){// 砍掉的树可以把剩下的树围起来 if(mv1>mv){//剩下树的价值要最大 l2=l1-l;nt=n;mv=mv1;ct=c;}else if(mv1==mv&&nt<=n){//价值相同时砍掉的树要最少 l2=l1-l;nt=n;mv=mv1;ct=c;}}return 0;
}
int main(){int n,i,j,k=0;int a,b,cnt,c;int mv1;while(scanf("%d",&n)!=EOF&&n){k++;nt=0;for(i=0;i<n;i++){scanf("%d%d%d%d",&s1[i].x,&s1[i].y,&s1[i].v,&s1[i].l);}mv=0;ct=0;for(j=1;j<(1<<n)-1;j++){//二进制枚举 //printf("%d\n",j);a=j,b=0;cnt=0;mv1=0;int l1=0;for(i=0;i<n;i++){if(((1<<i)&j)){//按位与 s[cnt++]=s1[i];//放入不砍的树 mv1+=s1[i].v;//剩余的价值 }else{l1+=s1[i].l;//可以做篱笆的长度 }}if(mv>mv1)//剩下的价值小于最优的价值 continue;do1(cnt,l1,mv1,j);}printf("Forest %d\n",k);printf("Cut these trees:");for(i=0;i<n;i++)if(!((1<<i)&ct))  printf(" %d",i+1);printf("\n");printf("Extra wood: %.2f\n\n",l2);}return 0;
}