更多细节请查看
https://www.zhihu.com/question/20455227

归一化的目的简而言之，是使得没有可比性的数据变得具有可比性，同时又保持相比较的两个数据之间的相对关系。
归一化首先在维数非常多的时候，可以防止某一维或某几维对数据影响过大，其次可以程序可以运行更快。

数据归一化应该针对属性，而不是针对每条数据，针对每条数据是完全没有意义的，因为只是等比例缩放，对之后的分类没有任何作用。

归一化的方法：具体可查看
http://blog.csdn.net/yudf2010/article/details/40779953
http://blog.csdn.net/facingthesuncn/article/details/17258415
http://blog.csdn.net/acdreamers/article/details/44664205
http://blog.csdn.net/junmuzi/article/details/48917361
http://blog.csdn.net/lkj345/article/details/50352385

Three common methods are used to perform feature normalization in machine learning algorithms.

Rescaling
The simplest method is rescaling the range of features by linear function. The common formula is given as:


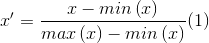
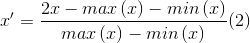
where x is the original value, x’ is the normalized value.

The equation (1) rescales data into [0,1], and the equation (2) rescales data into [-1,1].

Note: the parameters max(x) and min(x) should be computed in the training data only, but will be used in the training, validation, and testing data later.
我们必须使用同样的方法缩放训练数据和测试数据。例如，假设我们把训练数据的第一个属性从[-20,+20]缩放到[-1, +1]，那么如果测试数据的第一个属性属于区间[-30, +35]，我们必须将测试数据转变成[-1.5, +1.75]。

缩放的最主要优点是能够避免大数值区间的属性过分支配了小数值区间的属性。另一个优点能避免计算过程中数值复杂度。

线性函数转换将一系列数据映射到相应区间，例如将所有数据映射到1~100，可用下列函数
y=((x-min)/(max-min))*(100-1)+1；
min是数据集中最小值，max是最大值
同理若将所有数据映射到a~b，可用下列函数
y=((x-min)/(max-min))*(b-a)+a；

There are also some methods to normalize the features using non-linear function, such as

logarithmic function:

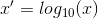
inverse tangent function:

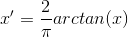
sigmoid function:

Standardization
Feature standardization makes the values of each feature in the data have zero-mean and unit-variance. This method is widely used for normalization in many machine learning algorithms (e.g., support vector machines,logistic regression, and neural networks). The general formula is given as:

where is the standard deviation of the feature .

举例说明（MATLAB）：

% X is train data;
X=[790 3977 849 1294 1927 1105 204 1329  768 5037 1135 1330 1925 1459 275 1487  942 2793 820 814 1617 942 155 976  916 2798 901 932 1599 910 182 1135  1006 2864 1052 1005 1618 839 196 1081];  
% 方法一
[Z,mu,sigma] = zscore(X)
%  方法二
[s t] = size(X)
Y=(X-repmat(mean(X),s,1))./repmat(std(X),s,1); %  Xnew is test data
[m n] = size(Xnew);
% 
Ynew = ((Xnew-repmat(mu,m,1))./repmat(sigma,m,1))

Scaling to unit length
Another option that is widely used in machine-learning is to scale the components of a feature vector such the complete vector has length one:

This is especially important if the Scalar Metric is used as a distance measure in the following learning steps.

3. Some cases you don’t need data normalization

3.1 using a similarity function instead of distance function

You can propose a similarity function rather than a distance function and plug it in a kernel (technically this function must generate positive-definite matrices).

3.2 Random Feforest

For random forests on the other hand, since one feature is never compared in magnitude to other features, the ranges don’t matter. It’s only the range of one feature that is split at each stage.

Random Forest is invariant to monotonic transformations of individual features. Translations or per feature scalings will not change anything for the Random Forest. SVM will probably do better if your features have roughly the same magnitude, unless you know apriori that some feature is much more important than others, in which case it’s okay for it to have a larger magnitude.

备注：
（1）在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。
（2）在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

不同类型数据要进行融合，也得将不同类型数据归一化处理后进行运算

关于python 实现归一化可参考
莫烦python - Sklearn
关于使用sklearn进行数据预处理 —— 归一化/标准化/正则化
机器学习中的数据预处理（sklearn preprocessing）

---

神经网络为什么要归一化?
具体可查看：
http://nnetinfo.com/nninfo/showText.jsp?id=37

随机森林是否需要归一化
具体可查看
https://www.quora.com/Should-inputs-to-random-forests-be-normalized?srid=3EJy&st=ns
http://stackoverflow.com/questions/8961586/do-i-need-to-normalize-or-scale-data-for-randomforest-r-package
http://stats.stackexchange.com/questions/41820/random-forests-with-bagging-and-range-of-feature-values

备注：
具体可查看
https://www.zhihu.com/question/20455227
https://www.zhihu.com/people/maigo
问题1：在进行数据分析的时候，什么情况下需要对数据进行标准化处理？
答：主要看模型是否具有伸缩不变性。

有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行标准化，以免模型参数被分布范围较大或较小的数据dominate。

有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如logistic regression。对于这样的模型，是否标准化理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行数据标准化。

具体可查看：
https://www.zhihu.com/question/30038463/answer/50491149

问题2：机器学习数据归一化的的方法有哪些？适合于什么样的数据？
答：
1. 最值归一化。比如把最大值归一化成1，最小值归一化成-1；或把最大值归一化成1，最小值归一化成0。适用于本来就分布在有限范围内的数据。
2. 均值方差归一化，一般是把均值归一化成0，方差归一化成1。适用于分布没有明显边界的情况，受outlier影响也较小。
具体可查看：
https://www.zhihu.com/question/26546711/answer/62085061

问题3：为什么 feature scaling 会使 gradient descent 的收敛更好?
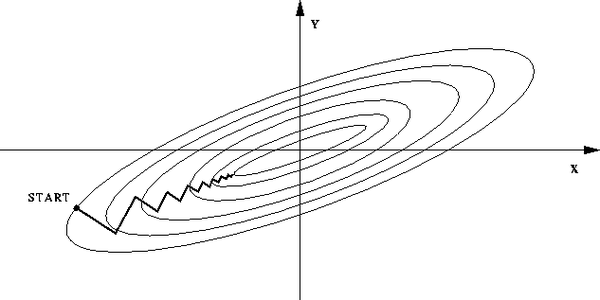
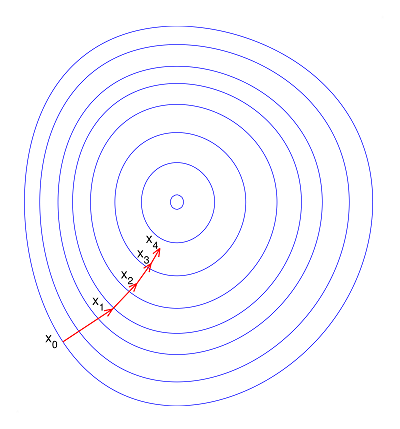
答：如果不归一化，各维特征的跨度差距很大，目标函数就会是“扁”的：

（图中椭圆表示目标函数的等高线，两个坐标轴代表两个特征）
这样，在进行梯度下降的时候，梯度的方向就会偏离最小值的方向，走很多弯路。

如果归一化了，那么目标函数就“圆”了：

看，每一步梯度的方向都基本指向最小值，可以大踏步地前进。
具体可查看：
https://www.zhihu.com/question/37129350/answer/70592743

问题4：数据特征的归一化，是对整个矩阵还是对每一维特征？
答：整体做归一化相当于各向同性的放缩，做了也没有用。
各维分别做归一化会丢失各维方差这一信息，但各维之间的相关系数可以保留。
如果本来各维的量纲是相同的，最好不要做归一化，以尽可能多地保留信息。
如果本来各维的量纲是不同的，那么直接做PCA没有意义，就需要先对各维分别归一化。
具体可查看：
https://www.zhihu.com/question/31186681/answer/50929278

MATLAB代码实现

http://blog.csdn.net/breeze5428/article/details/27308995
http://blog.csdn.net/yb536/article/details/41050181

function [X_norm, mu, sigma] = featureNormalize(X)  
%FEATURENORMALIZE Normalizes the features in X   
%   FEATURENORMALIZE(X) returns a normalized version of X where  
%   the mean value of each feature is 0 and the standard deviation  
%   is 1. This is often a good preprocessing step to do when  
%   working with learning algorithms.  % You need to set these values correctly  % ====================== YOUR CODE HERE ======================  
% Instructions: First, for each feature dimension, compute the mean  
%               of the feature and subtract it from the dataset,  
%               storing the mean value in mu. Next, compute the   
%               standard deviation of each feature and divide  
%               each feature by it's standard deviation, storing  
%               the standard deviation in sigma.   
%  
%               Note that X is a matrix where each column is a   
%               feature and each row is an example. You need   
%               to perform the normalization separately for   
%               each feature.   
%  
% Hint: You might find the 'mean' and 'std' functions useful.  
%     % let's calculate the total number of features    %mean([1; 2; 3; 4]) returns 2.5  %X(:,1) is the price of the houses  
%X(:,2) is the number of bedrooms  
%mu(1,1) = accessing the position of mu  
%mu(1,2) = 2  % updating the positions of a given matrix's column  
%d = [1 2; 3 4; 5 6]  
%d(:, 1) = d(:, 1) .- d(:, 1)  % As defined in the class notes, n is the number of features.  
n = size(X, 2);  % the given values of mu and sigma as initial zeros  
mu = zeros(1, n);  
sigma = zeros(1, n);  for featureColumn = 1:n  mu(1, featureColumn) = mean(X(:, featureColumn));  X(:, featureColumn) = X(:, featureColumn) .- mu(1, featureColumn);  sigma(1, featureColumn) = std(X(:, featureColumn));  X(:, featureColumn) = X(:, featureColumn) ./ sigma(1, featureColumn);  
end;  % updating the value of the return X_norm  
X_norm = X;  %disp(mu)  
%disp(sigma)  % ============================================================  end  

此外在matlab中也可以采用

[Z,mu,sigma] = zscore(X)

实现各个维度的标准化特征Ｚ。在求得mu和sigma后，如果新来一个特征向量ｘ，外面可以采用z = (x–mu)./sigma求得该向量的标准化向量。

matlab对训练集和测试集归一化

关于是否将训练集和测试集放在一起进行归一化有待讨论，若在一起，则会让测试集受到训练集的影响，导致训练集和测试集不相互独立。正确的做法是记录下训练集的归一化方法，用该方法对测试集单独进行归一化，matlab中的mapminmax函数提供了相应的机制。

对于一条新的数据，应该先按照训练集的归一化方法进行归一化，再进行分类。
可通过

inst = [1 2 3 4; 2 3 4 5; 3 4 5 6];
[inst_norm, settings] = mapminmax(inst);
test = [1 3 5]';
test_norm = mapminmax('apply', test, settings)test_norm =-1.0000
   -0.3333
    0.3333

解释说明：该数据inst为3行4列，每一列代表一个数据，每一行代表同一个属性，即数据个数为4个，属性个数为3个，由于归一化是针对于属性归一化的，所以每个属性都对于一个归一化的函数。
y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin，此时ymax=1，ymin=-1.

属性1：y=2*（x-1）/(4-1) + (-1);
属性2：y=2*（x-2）/(5-2) + (-1);
属性3：y=2*（x-3）/(6-3) + (-1);

那么对于test = [1 3 5]’归一化后，可得出相应的属性值为

属性1：y=2*（1-1）/(4-1) + (-1)=-1;
属性2：y=2*（3-2）/(5-2) + (-1)=-0.333;
属性3：y=2*（5-3）/(6-3) + (-1)=0.333;

这里的数据都是列数为样本个数，行数为属性个数。
其中settings记录了训练集的归一化方法，得到以下归一化结果
mapminmax会跳过NaN数据，最好的方法是归一化之后，将NaN赋值成0。

inst_norm(find(isnan(inst_norm))) = 0;

详情请查看
http://blog.csdn.net/lkj345/article/details/50352385

下面我们对mapminmax的用法进行详解

[Y,PS] = mapminmax(X)
[Y,PS] = mapminmax(X,FP)
Y = mapminmax('apply',X,PS)
X = mapminmax('reverse',Y,PS)

用实例来讲解,测试数据 x1 = [1 2 4], x2 = [5 2 3];

[y,ps] = mapminmax(x1)y =-1.0000   -0.3333    1.0000
ps = name: 'mapminmax'xrows: 1xmax: 4xmin: 1xrange: 3yrows: 1ymax: 1ymin: -1yrange: 2no_change: 0gain: 0.6667xoffset: 1

其中y是对进行某种规范化后得到的数据,这种规范化的映射记录在结构体ps中.让我们来看一下这个规范化的映射到底是怎样的?

Algorithm
It is assumed that X has only finite real values, and that the elements of each row are not all equal.

y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin;

[关于此算法的一个问题.算法的假设是每一行的元素都不想相同,那如果都相同怎么办?实现的办法是,如果有一行的元素都相同比如xt = [1 1 1],此时xmax = xmin = 1,把此时的变换变为y = ymin,matlab内部就是这么解决的.否则该除以0了,没有意义!]

也就是说对x1 = [1 2 4]采用这个映射 f: 2*(x-xmin)/(xmax-xmin)+(-1),就可以得到y = [ -1.0000 -0.3333 1.0000]
我们来看一下是不是: 对于x1而言 xmin = 1,xmax = 4;
则y(1) = 2*(1 - 1)/(4-1)+(-1) = -1;
y(2) = 2*(2 - 1)/(4-1)+(-1) = -1/3 = -0.3333;
y(3) = 2*(4-1)/(4-1)+(-1) = 1;
看来的确就是这个映射来实现的.
对于上面algorithm中的映射函数 其中ymin,和ymax是参数,可以自己设定,默认为-1,1;
比如

[y,ps] = mapminmax(x1);
ps.ymin = 0;
[y,ps] = mapminmax(x1,ps)y =0    0.3333    1.0000ps = name: 'mapminmax'xrows: 1xmax: 4xmin: 1xrange: 3yrows: 1ymax: 1ymin: 0yrange: 1no_change: 0gain: 0.3333xoffset: 1

则此时的映射函数为: f: 1*(x-xmin)/(xmax-xmin)+(0)

如果对x1 = [1 2 4]采用了某种规范化的方式, 现在要对x2 = [5 2 3]采用同样的规范化方式[同样的映射],如下可办到:

[y1,ps] = mapminmax(x1);
y2 = mapminmax('apply',x2,ps)y2 =1.6667   -0.3333    0.3333

即对x1采用的规范化映射为: f: 2*(x-1)/(4-1)+(-1),(记录在ps中),对x2也要采取这个映射.
x2 = [5,2,3],用这个映射我们来算一下.
y2(1) = 2(5-1)/(4-1)+(-1) = 5/3 = 1+2/3 = 1.66667
y2(2) = 2(2-1)/(4-1)+(-1) = -1/3 = -0.3333
y2(3) = 2(3-1)/(4-1)+(-1) = 1/3 = 0.3333

X = mapminmax(‘reverse’,Y,PS)的作用就是进行反归一化,讲归一化的数据反归一化再得到原来的数据:

[y1,ps] = mapminmax(x1);
xtt = mapminmax('reverse',y1,ps)xtt =1     2     4

详情可查看
http://www.ilovematlab.cn/thread-47224-1-1.html
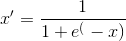
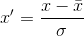
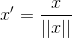