前言

头部驱动除了之前关注的表情驱动外，还有眼球驱动和头部方向驱动。本博客基于opencv官方文档和部分开源代码来研究如何基于人脸关键点获取头部的朝向。

国际惯例，参考博客：

opencv:Camera Calibration and 3D Reconstruction

opencv:Real Time pose estimation of a textured object

cv.solvePnP位姿估计旋转向量精度分析

头部姿态估计原理及可视化

重磅！头部姿态估计「原理详解 + 实战代码」来啦！

相机矩阵(Camera Matrix)

Python cv2.decomposeProjectionMatrix方法代码示例

face_landmark

head-pose-estimation

Face-Yaw-Roll-Pitch-from-Pose-Estimation-using-OpenCV

talking-head-anime-demo

OpenVtuber

相机标定理论

几种坐标系

先看从opencv官网中扒下来的两幅图，代表针孔相机模型(pinhole camera model)

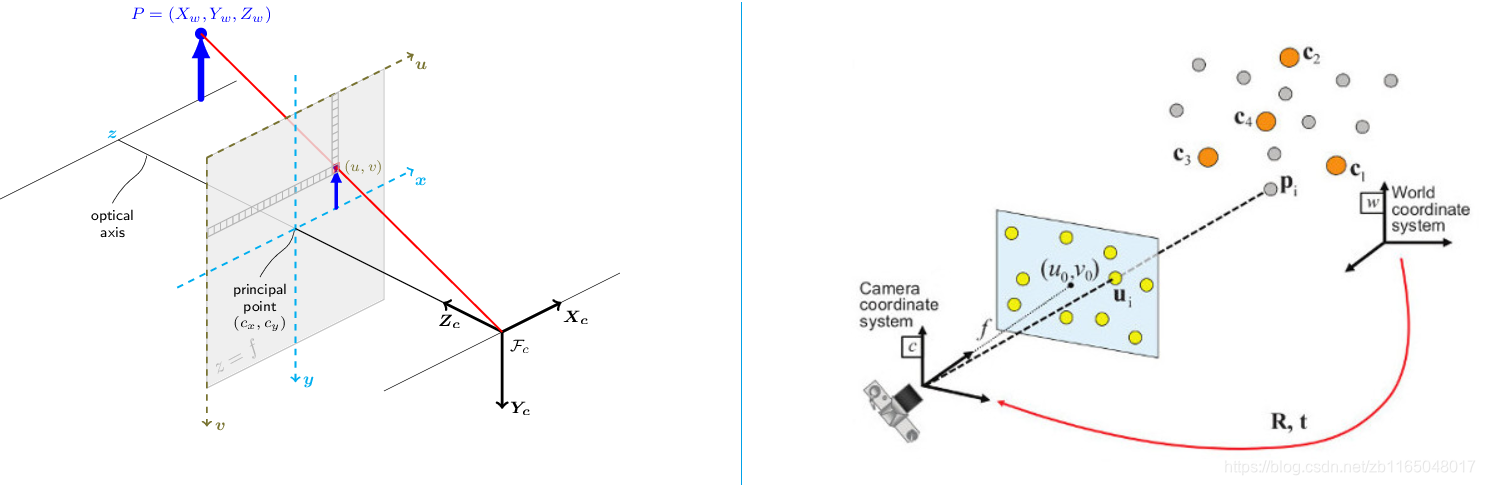
其中涉及到几种坐标系：

• 世界坐标系：一个固定不变的坐标系，原点通常固定不变，右图的$w$坐标系
• 相机坐标系：相机在世界坐标系下的姿态，右图的$c$坐标系
• 图像坐标系：成像平面，图中的x-y坐标轴，其原点是相机的光轴与成像平面的胶垫
• 像素坐标系：最终图像，图中的u-v坐标轴，原点在左上角，就跟opencv输出的图片一样，左上角代表$(0,0)$像素位置。

图像坐标系和像素坐标系横轴和纵轴方向一致，但是单位不同，一个是物理单位，一个是像素单位，一般有一个对应的缩放关系，代表一个像素在成像平面上的大小。

针孔相机的目标就是把3D坐标点$P_w$利用透视变换(perspective transformation)投影到图像平面上，得到对应像素$p$。其中$P_w$和$p$都在齐次坐标系下表示。

无畸变情况下，针孔相机的投影变换可以表示为：
$$sp=A[R|t]P_w$$
其中$P_w$为世界坐标系下的3D坐标点，$p$是图像平面上的2D像素点，$A$是相机内参矩阵，$R$和$t$分别描述了世界坐标系到相机坐标系的旋转和平移变换，$s$是任意尺度的投影变换(非相机模型的参数，其实就是图像坐标系到像素坐标系的变换系数)。

世界坐标系到相机坐标系

旋转-平移矩阵$[R|t]$是投影变换(projective transformation)和齐次变换(homogeneous transformation)的乘积。

维度为$(3,4)$投影变换可以将相机坐标系里的3D坐标映射到成像平面的2D坐标，并且在归一化的相机坐标系$x^{\prime }=\frac{X_c}{Z_c}$和$y^{\prime }=\frac{Y_c}{Z_c}$下表示出来
$$Z_c\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]$$
而齐次变换通常在相机外参$R$和$t$中体现出来，代表世界坐标系到相机坐标系的变换，因此给定一个世界坐标系下的点$P_w$，那么相机坐标系下的对应点为:
$$P_c=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]P_w$$
这个齐次变换一般就是由一个(3,3)的旋转矩阵和一个(3,1)的平移向量组成：
$$\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\\ 0& 0& 0& 1\end{array}\right]$$
因此
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
结合投影变换和齐次变换，就可以得到将世界坐标系下3D点映射到归一化相机坐标系下的成像平面下2D点的变换：
$$Z_c\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=[R|t]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
其中$x^{\prime }=\frac{X_c}{Z_c}$，$y^{\prime }=\frac{Y_c}{Z_c}$

相机坐标系到像素坐标系

相机内参矩阵$A$通常用K表示，用于将相机坐标系下的3D坐标点投影到像素坐标系中。
$$p=A{P}_c$$
通常相机内参矩阵$A$包含了以像素为单位的焦距$f_x$和$f_y$，以及靠近图像中心的原点$(c_x,c_y)$：
$$A=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$
所以
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$
相机内参，顾名思义只与相机自身有关，与外部环境无关，所以一次标定以后，只要你不动焦距，就可以永久使用。

总结：世界坐标系到像素坐标系

将内外参矩阵放在一起就能把$sp=A[R|t]P_w$重写成：
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
如果$Z_c\ne 0$，那么
$$\left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{c}{f}_x{X}_c/Z_c+c_x\\ f_y{Y}_c/Z_c+c_y\end{array}\right]$$
其中
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=[R|t]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
就得到最开始描述的左图中的u-v坐标系映射模型了。

【注】上述理论是基于畸变参数为0的情况下，关于不为零的时候，请自行查阅opencv官方文档描述或者其他资料。

头部姿态估计

理论

通过内外参矩阵可以将世界坐标系下的3维点映射到成像平面，那么同理，可以利用相机内参、世界坐标系的3D点、成像平面的2D点，找到世界坐标系到相机坐标系的旋转和平移(外参矩阵)。

在做头部姿态估计的时候，我们仅仅知道人脸关键点，其它信息一无所知，那么应该怎么求解呢？

通过后五篇参考博客的源码分析，大致流程就是：

• 建立一个虚假的3D头模，找到几个人脸关键点的3D坐标
• 假定当前相机的内参矩阵和畸变系数
• 利用solvePnP求解平移向量和旋转向量
• 利用decomposeProjectionMatrix将旋转向量转换为欧拉角

其中solvePnP的函数描述如下：

retval, rvec, tvec	=	cv.solvePnP(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, flags]]]]	)

输入参数：

• objectPoints：世界坐标系下的3D坐标
• imagePoints：2D投影坐标
• cameraMatrix：相机内参矩阵
• distCoeffs：畸变系数

输出：

• rvec：旋转向量，可使用Rodrigues转换为旋转矩阵
• tvec：平移向量

其中decomposeProjectionMatrix的函数描述如下：

cameraMatrix, rotMatrix, transVect, rotMatrixX, rotMatrixY, rotMatrixZ, eulerAngles	=	cv.decomposeProjectionMatrix(	projMatrix[, cameraMatrix[, rotMatrix[, transVect[, rotMatrixX[, rotMatrixY[, rotMatrixZ[, eulerAngles]]]]]]]	)

输入参数：

• projMatrix：维度为$(3,4)$的投影矩阵$P$

返回参数：

• cameraMatrix：内参矩阵
• rotMatrix：外部旋转矩阵
• transVect：外部平移矩阵
• rotMatrixX：绕x轴旋转的矩阵
• rotMatrixY：绕y轴旋转的矩阵
• rotMatrixZ：绕z轴旋转的矩阵
• eulerAngles：旋转欧拉角

实现

例如最后一个参考博客中的源码解析分别为：

• 预加载3D人脸关键点模型

  首先预加载一个3D人脸关键点模型，源码提供了人脸的39个关键点，我提取了其中12个关键点，关键点坐标如下：

  array([[ 29.64766 ,  10.      ,  66.01275 ],[126.870285,  10.      ,  66.01275 ],[ 60.359673,  34.85047 ,  44.13414 ],[ 25.144653,  33.933437,  39.87654 ],[ 96.15827 ,  34.85047 ,  44.13414 ],[131.37329 ,  33.933437,  39.87654 ],[ 78.25897 ,  88.78672 ,  67.6343  ],[ 50.51882 , 109.59447 ,  50.48531 ],[ 78.25897 , 105.25116 ,  67.04956 ],[105.99912 , 109.59447 ,  50.48531 ],[ 78.25897 , 119.950806,  60.976673],[ 78.25897 , 162.94363 ,  40.70434 ]], dtype=float32)
  

  原始39个关键点与对应提取的12个关键点在2D图像上的位置关系如下：

  

• 提取真实人脸关键点

  利用opencv或者HRNet模型，提取真实图像中的2D人脸关键点，可参考之前换脸的博客，或者去我github上找源码也可以，效果如下：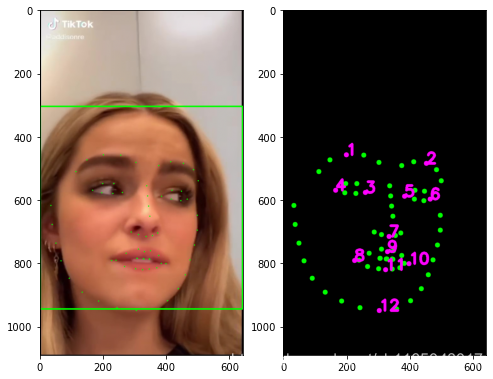

  

• 计算朝向
  首先创建内参矩阵：

  H,W = img.shape[0],img.shape[1]
  matrix = np.array([[W,0,W/2.0],[0,W,H/2.0],[0,0,1]])
  

  然后求解外参矩阵，调用solvPnP函数求解旋转向量和平移向量

  _,rot_vec,trans_vec = cv2.solvePnP(obj[pick_model,...].astype("float32"),points[pick_dlib,...].astype("float32"),matrix,None,flags=cv2.SOLVEPNP_DLS)
  

  将旋转向量和平移向量组合成外参矩阵的形式

  rot_mat = cv2.Rodrigues(rot_vec)[0]
  pose_mat = cv2.hconcat((rot_mat, trans_vec))
  

  最后将旋转向量转换为欧拉角：

  
  euler_angle = cv2.decomposeProjectionMatrix(pose_mat)[-1]
  

  可视化效果如下：

后记

结果有时候受到你初始模型的影响，所以建议多找些源码测试一下，找到一个合适的3D模型使用。而且在驱动卡通角色时候，由于建模和游戏引擎的原因，坐标系可能不同，因而欧拉角也要做适当的变换，比如我的项目基于python和unity交互的卡通角色肢体和表情驱动(深度学习)中关于表情驱动部分的实验。

完整的python实现放在微信公众号的简介中描述的github中，有兴趣可以去找找。同时文章也同步到微信公众号中，有疑问或者兴趣欢迎公众号私信。