一)字母大小写全排列
784. 字母大小写全排列 - 力扣(LeetCode)
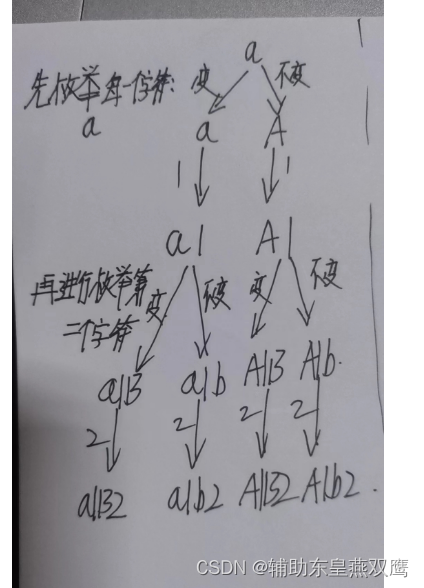
1)从每一个字符开始进行枚举,如果枚举的是一个数字字符,直接忽视
如果是字母的话,进行选择是变还是不变
2)当进行遍历到叶子结点的时候,直接将结果存放到ret里面即可
3)相对于是对于这个决策树做一个深度优先遍历
class Solution {List<String> ret=new ArrayList<>();StringBuilder path=new StringBuilder();public List<String> letterCasePermutation(String s) {char[] array=s.toCharArray();dfs(array,0);return ret;}public void dfs(char[] array,int index){if(path.length()==array.length){ret.add(path.toString());return;}if(index>=array.length) return;//选if(array[index]>='0'&&array[index]<='9'){path.append(array[index]);dfs(array,index+1);path.deleteCharAt(path.length()-1);}else{path.append(array[index]);dfs(array,index+1);path.deleteCharAt(path.length()-1);if(array[index]>='a'&&array[index]<='z')path.append((char)(array[index]-32));elsepath.append((char)(array[index]+32));dfs(array,index+1);path.deleteCharAt(path.length()-1);}} }
二)优美的排列
526. 优美的排列 - 力扣(LeetCode)
1)每一层开始就是从第一个数开始将所有的数进行枚举一遍,只要这个数没有使用过,就可以把这个数放在这里面试一试
2)还是需要判断一下这个数能否整除下标或者是能够被下标整除,只要上面的条件有一种情况不满足,那么就进行剪枝操作;
3)函数的递归出口:当遇到叶子节点的时候,直接返回结果
class Solution {List<List<Integer>> ret=new ArrayList<>();List<Integer> path=new ArrayList<>();boolean[] check;public int countArrangement(int n) {check=new boolean[n+1];dfs(n,1);return ret.size();}public void dfs(int n,int pos){if(path.size()==n){ret.add(new ArrayList<>(path));return;}for(int i=1;i<=n;i++){if((i%pos==0||pos%i==0)&&check[i]==false){path.add(i);check[i]=true;dfs(n,pos+1);path.remove(path.size()-1);check[i]=false;}}} }
三)N皇后:
51. N 皇后 - 力扣(LeetCode)
第一种画决策树的方法:
先考虑第一个格子能不能进行存放,当进行考虑下一个格子的时候,是进行挨着考虑的,一个格子一个格子看看能不能进行存放
第二种画决策树的方法:是通过一行一行的来进行考虑的
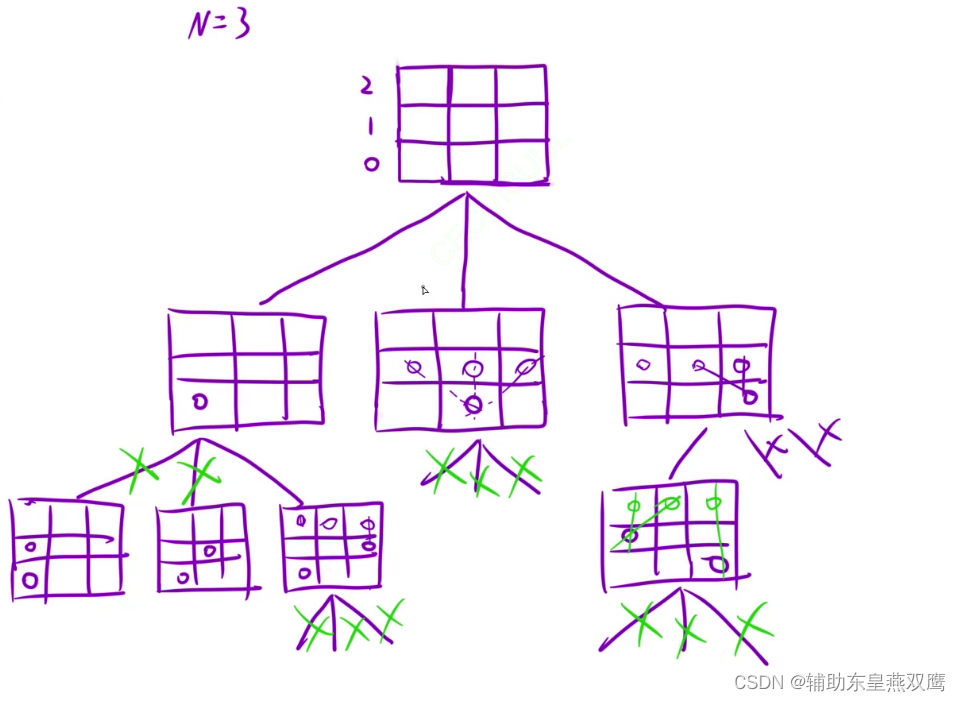
此时我不是一个格子一个格子的进行考虑,这一次我一次考虑一行,我只考虑第0行的皇后应该摆放在那里,应该只考虑第一行的皇后摆放在哪里,第二行的皇后应该摆放在那里,第三行的皇后应该摆放在那里,下面我们进行考虑一下当N=3的时候:
1)首先我们第一步应该考虑一下,第0行的皇后可以放在哪里,这个时候又出现三种情况可以放在(0,0)可以放在(0,1),还可以放在(0,2)
2)然后再次进行考虑,当我们第0行的三个皇后已经放好的情况下,那么此时再来进行考虑第一行,正常情况下如果不出现剪枝的情况,第一行也是可以存放三个位置的分别是(1,0),(1,1)和(1,2),但是此时考虑剪枝,这个时候就出现了,某一个行上面有两个皇后,对角线上面有两个皇后
每一层在做的事情:你给我一个行数,我在这一行内每一个格子存放一个皇后,如果我能够存放,我就把这个皇后放在这里没然后进行考虑下一行
递归出口:当我们枚举行数发生越界的时候,此时说明就已经得到了合法的情况,此时就可以把这个合法的情况加入到我们最终的结果中即可
如何剪枝:剪枝的目的就是考虑当前这个位置是否可以能够放上皇后
1)无脑循环:假设当前这个这个位置可以存放皇后,首先来判断这一行有没有放皇后,这一列有没有放皇后,这个皇后的左对角线有没有放皇后,这个皇后的右对角线有没有放皇后,时间复杂度是4n*2^n
在这种决策树的画法里面,我们是每一行每一行的来进行列举的,所以当我们进行列举这一行上面的三个位置的时候,是一定不会出现在这一行上面的;
2)类似于哈希表的策略:在这里面只是需要搞一个boolean数组就可以搞定这个题了
boolean checkcol[]=new boolean[n],如果在第一列上放了一个皇后,那么只是需要让这一列变成true即可,那么就是checkcol[1]=true,说明这一列已经有皇后了,所以使用布尔数组可以快速判断某一列是否有皇后了
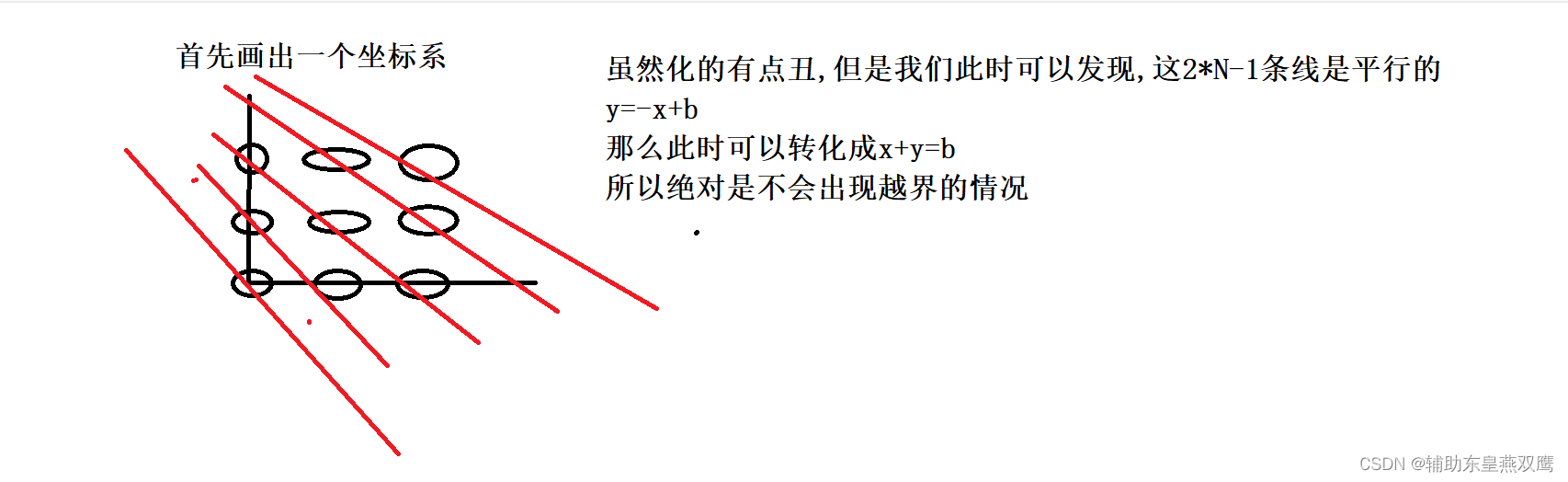
3)判断对角线以及副对角线的策略:使用布尔数组+数学来进行解决
四)有效的数独:
36. 有效的数独 - 力扣(LeetCode)

Node.js - 模块化)

 - RabbitMQ队列类型、死信消息与死信队列、懒队列、集群模式、MQ常见消息问题)

—— StarGAN(1))



 - springboot)






Spring Boot 配置文件的探索之旅)

)

—matlab基本语句)